Solving multicast routing problem Using Particle Swarm Optimization

 

Prasanta Kumar Raut ¹, Siva Prasad Behera ¹

 

¹ Department of Mathematics, C.V. Raman Global University, Bhubaneswar-752054, Odisha, India

 

 

1. INTRODUCTION

There exist many routes from a source to a destination in a given graph but finding the optimum route at the lowest cost is extremely difficult. The term “swarm” comes from the field of artificial intelligence. In swarm intelligence, there are a number of shortest path techniques used to overcome this problem. Many research papers are available to tackle routing problems using PSO Rehab and Abdel-Kader (2011), all of which employ the same technique but use various particles encoding in the discrete form Baburaj and Vasudevan (2008). To tackle this problem, we designed a simple encoding approach it breaks the space into smaller space of reduced size after that combine all the results for evaluating the optimal path, it works on the the greedy approach principle.

 

2. USE OF PARTICLE SWARM OPTIMIZATION

Swarms are a group of particles in PSO that are used to discover the shortest path from source to destination of a network. Every particle has an initial location (its current position in time), a personal best position (its best position among all particles in search space), and associated   velocity of every particle. During this method, every particle tries to move towards the particle closest to the optimal solution, but the best solution is obtained from Xu et al. (2007)

 

                           (1)

 

                                                                                                                (2)

 

In the swarm, i=1,2,3,4……n and Pi_pest is the particle best solution, where g(ibest)is the global best solution, v is the particles velocity and p,g are control parameters that regulate the particle’s efficiency

 

3. PSEUDO CODE OF MULTICAST PSO

Assume that G is a multicast tree

             The initial root of the multicast tree is denoted by symbol “S”

              D is the final root multicast tree

Create an initial swarm at random

·        Continuing for each particle i until you have reached the maximum number of iterations

Calculate the best fitness value possible.

·        Best position should be updated.

1)     Velocity update

2)     Refresh the global position

Until the threshold termination is reached

 

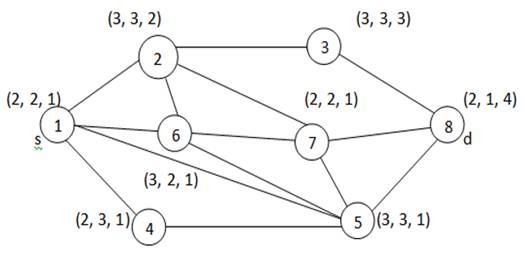
4. (A)PSO TO SOLVE MULTICASTING NETWORK WITH VERTICES WITH TRIANGULAR FUZZY NUMBER

 

Figure 1                  

                                                                                           

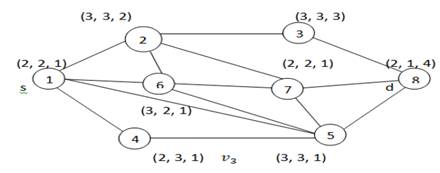
Figure 1 Multicast Network

    

To solve multicast routing problem by using PSO, in this network vertex   is a source vertex and  called destination vertex .In starting iteration of PSO we have initially determined the random route from source to destination because every particle associated in multicast network has capable to give the solution of problem .In initial stage network break the paths sequentially into small space.

Table 1

Table 1
Route number	Route list
1	1-2-7-8
2	1-6-7-8
3	1-6-5-8

                                                      

Consider the starting velocity of each particle is zero in equation (2), for which the “P best “defines initial routes as the current best paths of particles as follows

 

                                                       P _best =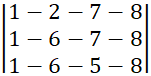

 

From the above three particle we have to find the global best of the particles which have minimum cost among all particles .minimum cost of the particle we can find by using Euclidean distance between two configurations s = (, .....) and t = (,.....) in euclidean space. i.e., Mathematically define by

 

                                                                             

 

we get G_best is 1−6−7−8, by using Euclidean distance formula

Now velocity of particle (vpart) is evaluated by taking the difference between G_best & P_best

  Now consider particle velocity associated in path 3 in Table 1

 

V _part [3] [] = G _best []- P _best []

 

V _part [3] [] = (1 6   7   8) – (1   6   5    8)

 

                                                                = 7

 

Similarly, the particle’s velocity can be determined for path -1, path-2 and path-3 in Table 1 obtained as follows

 

 

 

                                                                 V _part [] [] =

 

The position of each particle is updated in accordance with the new velocity. Final result, the procedure for modified the position s of all particles associated network in Figure 1 is defined as

 

C _part [] [] =   V _part [] [] + C _part [] []

For last (3^rd) particle we find the new position

 

C _part [] [] = (7) + (1 6 5 8)

 

C _part [] [] = (1 5 6 7   8)

 

The three p-best represented in Figure 1 by dark line. Using a dark dashed line ,one G is preferable .Following the update of the second particle ,we now have a set of nodes from which we can try to discover a route from source to destination .one advantage of this strategy is that we don’t have to search all nodes in the network ;instead, we only have to explore paths between these nodes .As a result ,all networks are divided into little networks, and we search inside this small group of networks ,with the node positions of these small closed networks changing by  dynamically .when the associated particle’s velocity and position are changes simultaneously ,every   particles eventually produce a better solution.

 

C _part [3] [] = 1-5-7-8

 

Figure 2

                                                                          

Figure 2

 

 

 

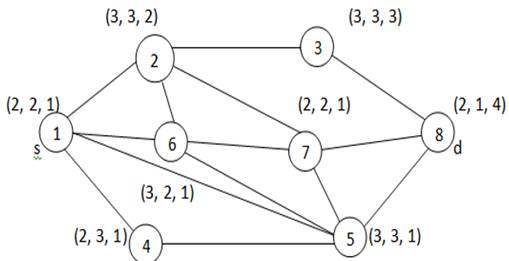
Figure 3

                                                                       

Figure 3 The network cost path is lowered from 6.62 to 5.17 after updating particle 1-2-7-8 to 1-2-3-8

          

 Figure 4

                                                                       

Figure 4 Network after updating

 

Position of particle is changed from (1,2,3,8) to (1,2,7,8) by doing cost path reduced from 6.62 to 5.17 which is shown in Figure 2. similarly, Figure 3 show path of third particle position is update from (1,6,5,7,8) to (1,5,7,8) and cost of path is modified from 6.16 to 5.15

 

Simulation Result

There are 35 nodes in this example, and each link connecting the nodes has a cost. To test the influence of particles, two simulation procedures were used. The first simulation uses 10 particles,30 nodes, and 40 iterations, whereas the second uses 15 particles, 35 nodes, and 40 iterations.

Figure 5 shows that the cost of the path is 45 after 10 iterations, but after 50 iterations, the minimal cost path is 12, which is the network’s ideal path.  At 10th iteration the cost route in the network is 35, while in 8 in the 50 iterations, as seen in the second Figure 6. As a result of which we obtain a decent path in the second iteration because they have spread so widely in the network

 

Figure 5

                                                                      

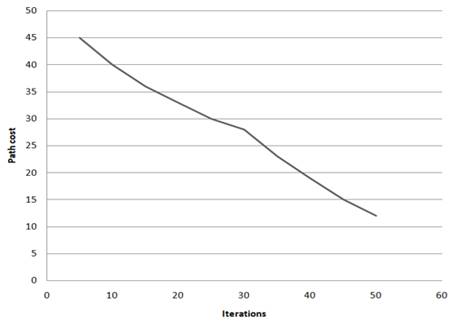
Figure 5  Simulation Result of 10 Particles

 

Figure 6

                                                                             

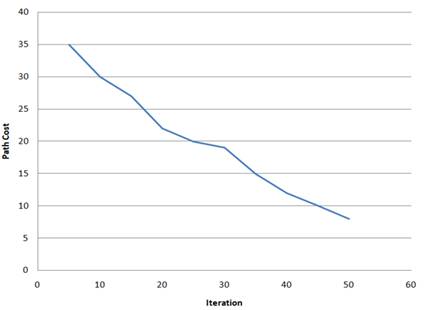
Figure 6 Simulations Result Of 15 Particles

                                   

5.  CONCLUSION

Many approaches to solve the routing problem using PSO have been described, but this one stands out since it uses simple encoding particles and is straight forward to implement. when by increasing the number of particles or iterations, the result is more accurate. This method can be implemented to tackle not only routing but also discrete problems.

 

Conflicts Of Interest

The authors declare that they have no conflicts of interest.

 

Acknowledgment

This research is supported and funded by C.V Raman Global University, Bhubaneswar, Odisha, India.

 

REFERENCES

Ahn, C.W. Ramakrishna, R.S. (2002). A Genetic Algorithm for Shortesh Path Routing Problem And Sizing of Populations, Ieee Transactions on Evolutionary Computation. 6(6). https://doi.org/10.1109/TEVC.2002.804323

Baburaj, E. and Vasudevan, V. (2008). An Intelligent Mesh Based Multicast Routing Algorithm for MANETs using particle Swarm Optimization, IJCSNS International Journal of Computer 214 Science and Network Security, 8(5).

Behera, S.P.  Pati, J.K. Raut, P.K. and Mahanta, K.L. (2022). Calculation of Linear Fractional Fuzzy Transportation Problem Using Simplex Method. International Journal of Engineering Science Technologies, 6(2), 38-47. https://doi.org/10.29121/ijoest.v6.i2.2022.302

Behera, S.P. Mishra, D. Bhattacharjee, S. Raut, P.K. (1969). A Modified Approach in Shortest Path Algorithm, International Journal of Advance Research, Ideas and Innovations in Technology, 7(4), 1489-1493.  

Raut, P.K. Behera, S.K. Pati, J.K. (2021). Calculation of Shortest Path in a Closed Network in Fuzzy Environment, International Journal of Mathematics Trends and Technology, 67(11), 31-37. https://doi.org/10.14445/22315373/IJMTT-V67I11P504

Raut, P.K. Behera, S.P. (2021). Application of Fuzzy Optimal Path Algorithm for Bus Route Expansion in Bhubaneswar city, Odisha, International Journal of Research Culture Society Issn, 5(11).  

Rehab, F. and Abdel-Kader, (2011). An Improved Discrete PSO with GA Operators for Efficient Qos- Multicast Routing, International Journal of Hybrid Information Technology, 4(2). https://doi.org/10.1016/j.asej.2011.05.002

Sombuntham, P. and Kachitvichayanukul, V. (2010). A Particl Swarm Optimization Algorithms for Multi-depot Vehicle Routing problem with Pickup and Delivery Requests. https://doi.org/10.1063/1.3510581

Xu, Y. Hu, J. Hirasawa, K. Pang, X. (2007). A New Cooperative Approach to Discrete Particle Swarm Optimization, SICE Annual Conference. https://doi.org/10.1109/SICE.2007.4421186

Xue, G. (2003). Minimum Cost Multicast and Unicast Routing in Communication Network, Ieee Transactions on Communications, 51(5). https://doi.org/10.1109/TCOMM.2003.811420