Date of Patent: Mar. 17, 2020) Yoshimura et al. (2018a) or ultra-high-temperature and pressure cavitation (UTPC) Yoshimura et al. (2018b). It should be noted that both MFC and UTPC operate on the same principles but differ in the dimensions of the equipment used. These techniques are able to generate compressive residual stress on material surfaces, improve corrosion resistance and oxidation resistance, and form tough layers that resist cracking. Using these methods, our group has modified the surfaces of low alloy steels, aluminum alloys Yoshimura et al. (2021a), magnesium alloys Ijiri et al. (2021), Ni-based superalloys and titanium dioxide particles Yoshimura et al. (2018a).

Previous work has demonstrated that MFC processing in which water jet cavitation (WJC) is combined with ultrasonication in deuterated acetone could potentially result in bubble fusion Yoshimura et al. (2018c). However, it is unlikely that the pressures that are generated during bubble shrinkage will exceed the threshold pressure required for bubble fusion or that the energy density of the atoms in the bubbles during bubble shrinkage will exceed the fusion threshold. In addition, because deuterated acetone is expensive, prior work showed that it is necessary to reduce the size of the equipment.

In the present study, reduced size UTPC equipment was prototyped. UTPC processing was subsequently performed by applying a strong magnetic field during cavitation, which was found to increase the pressure associated with bubble shrinkage. The possibility that this process would cause the bubble pressure to exceed the threshold value necessary for fusion was studied. We also investigated the likelihood that the energy density of the atoms in the bubble during bubble shrinkage would exceed the value necessary for fusion.

 

2. EXPERIMENTAL

2.1 PROTOTYPE REDUCED SIZE UTPC EQUIPMENT

WJC has a peening effect that imparts compressive residual stress to the surface of a material due to the very high pressures generated during the collapse of microjets near the surface Kling (1970), Summers (1987). In the case that ultrasonic waves are applied to WJC bubbles, isothermal expansion occurs when the pressure around the bubbles exceeds Blake threshold Atchley 1989. Therefore, the bubbles are able to overcome the effects of surface tension (that is, Laplace stress) and expand significantly in the case that A ≥ A_Blake, where A_Blake is the Blake threshold Atchley 1989. During this process, the isothermal expansion and adiabatic compression of bubbles produce so-called hot spots Gompf et al. (1997) generated in the microjets at which chemical reactions can occur, resulting in mechanical and electrochemical effects. This series of events represent the basic principle of MFC. The accompanying bubble temperatures can be estimated by sonoluminescence (SL). This is a phenomenon in which pulsating bubbles, which can concentrate diffuse sound energy by a factor of 12 orders of magnitude Barber and Putterman (1991), produce very short flashes of ultraviolet light Barber et al.  (1997), Putterman and Weninger (2000).

Various techniques have been developed to raise the temperature and pressure of cavitation bubbles during the MFC process. Although these trials have used water as the liquid medium, the basic results can also be applied to other liquids such as deuterated acetone. The pump discharge pressure is an important factor in the production of high-pressure microjets, and a pressure of 35 MPa or higher is required to obtain the high collapse pressure of the microjet. The number of cavitation bubbles depends on the flow rate of the liquid, while the diameter of the liquid jet nozzle affects the size of the cavitation bubbles as well as the flow rate and speed of the liquid jet Yoshimura et al. (2021b). The diameter of the nozzle used to perform surface modification in a UTPC system is 0.8 mm. However, in order to achieve a discharge pressure of 35 MPa with this nozzle diameter, a flow rate of 7 L/min is required, which necessitates a large reaction vessel. This, in turn, leads to economic challenges related to the use of deuterated acetone. For these reasons, a prototype bubble fusion apparatus was designed to provide a more compact MFC process Yoshimura et al. (2021c) based on a 0.1 mm nozzle with a flow rate of 150 mL/min. This device was originally developed to permit nano-level processing of titanium oxide, which is a photocatalytic material, in conjunction with SL measurements during MFC. This work reduced the overall size of the equipment. As shown in Figure 1, a swirl flow nozzle (SFN) [4] was mounted on the liquid jet nozzle to increase the size of the liquid jet cavitation generated from the 0.1 mm nozzle.

Table 1 summarizes the specifications for the prototype small-scale bubble fusion equipment. Figure 1 presents a diagram of the equipment designed by 3D-CAD, while Figure 2(a) provides a photographic image of the exterior of the apparatus. During operation of this equipment, the reaction vessel was evacuated in order to degas the deuterated acetone, using a rotary pump. The apparatus used in the experiments with a 0.1 mm nozzle also included a high-pressure pump (L. TEX Corp., LTEX8731E) having a maximum pressure of 40 MPa and a maximum discharge rate of 200 mL/min together with 50 W ultrasonic transducers (Honda Electronics Corp., WSC28TH, HEC-45282) each having a frequency of 28 kHz and an output power of 40 W. Because the UTPC device was equipped with a swiveling water jet nozzle, the bubbles underwent a greater expansion so that the UTPC process was realized Yoshimura et al. (2018b). Acetone was supplied from a holding tank to the high-pressure pump and a 40 MPa acetone jet was ejected from the WJ nozzle. Figure 2(c) and 2(d) show photographic images of the MFC process using acetone. During operation of this equipment, bubbles were generated in the acetone and underwent coalescing growth near the center of the nozzle with occasional coalescence and growth at more distant locations. In future work, our group intends to examine the mechanism by which these bubbles in acetone form aggregated chain structures that are not observed in water

Table 1 Specifications of prototype small-scale bubble fusion equipment

 

 

Figure 1 Schematic diagram of the prototype small-scale bubble fusion equipment

 

Figure 2 Photographic images of (a) the prototype small bubble fusion equipment and (b, c) the resulting MFC bubbles

 

2.2 ACTIVATION OF THE MFC BUBBLES BY A STRONG MAGNETIC FIELD

A basic experiment concerning the activation of MFC bubbles was carried out by applying a strong magnetic field at atmospheric pressure while using the reduced size MFC equipment equipped with a 0.1 mm nozzle. As noted, this apparatus was previously developed for nano-level processing of titanium oxide in conjunction with SL measurements. The field was applied by placing two strong neodymium permanent magnets (Sangyo Supply Co., Ltd., N40) at the base of the device, facing the water jet nozzle. These magnets had dimensions of 20 mm × 7 mm × 10 mm (± 0.1 mm) and were magnetized along the 10 mm thickness direction. After applying these magnets, jets of pure water showed an increase in the number of bubbles, demonstrating that the WJC process was activated in the presence of a strong magnetic field.

During the MFC process, high-temperature, high-pressure bubbles were generated containing H+, OH- and electrons due to the thermal decomposition of water vapor, and these charged species were affected by the Coulomb force imparted by the magnetic field. Throughout the cavitation process induced by the WJ nozzle, bubbles were repeatedly generated, grew and collapsed, and the collapse of these cavitation bubbles produced many new bubbles to form a cavitation cloud. The Coulomb force imparted by the magnetic field likely promoted collisions between bubbles during bubble collapse, leading to an increase in the number of bubbles that were generated and further development of the cavitation cloud. To date, the activation of liquid cavitation bubbles in this manner has not been reported, although there has been research regarding SL in the presence of high magnetic fields Young et al. (1996). During trials in water, changes in the magnetic field at a constant sound pressure have been found to cause the SL signal to disappear when a threshold magnetic field value is exceeded. It has also been shown that varying the sound pressure with a fixed magnetic field dramatically increases the upper and lower limits of the pressure around the bubble that define the range over which SL will appear Young et al. (1996).

Placing two neodymium magnets at the base of the water tank against the nozzle outlet (as shown in Figure 2) was found to generate a magnetic flux density at the nozzle outlet of 0.23 mT. During the actual trials, four magnets were affixed to the vertical wall surface of the nozzle part of the apparatus while another four magnets were applied to both sides of the water vessel wall at the position at which the cavitation cloud was formed. A further four magnets were placed on the vertical wall surface where the ultrasonic transducer was located, for a total of 14 magnets. It should be noted here that the S pole N pole magnetic circuit was constructed so that the polarities of the opposing surfaces were different, and so the magnetic flux at the nozzle outlet was increased to 1.2 mT. It is also important to note that increasing the number of magnets would be expected to generate a higher magnetic field of 100 mT or more at the nozzle outlet.

Employing an odd number of ultrasonic transducers that produced ultrasonic waves from the periphery to the center of the liquid jet in conjunction with the strong magnetic field from the nozzle outlet to the cavitation cloud generated cavitation bubbles having a high energy density. It was anticipated that this phenomenon would occur in deuterated acetone as well as in water so that bubble fusion could be realized.

 

3. BUBBLE FUSION THEORY

3.1 BUBBLE PRESSURE AND TEMPERATURE

  The Keller-Miksis formulation Keller and Miksis (1980),  Gaitan et al. (1992)is an equation describing the large, radial oscillations of a bubble trapped in a sound field. When the frequency of the sound field approaches the natural frequency of the bubble, large amplitude oscillations will occur. This equation takes into account viscosity, surface tension, incident sound waves and acoustic radiation coming from the bubble. The latter factor was not previously incorporated in Lauterborn's calculations based on the equation that Plesset et al. modified from Rayleigh's original analysis Rayleigh (1917), Plesset (1949) of large oscillating bubbles Keller and Miksis (1980). Keller and Miksis obtained the equations Gaitan et al.  (1992):

 

 

 

 

 

       (1)

and

                                                                                                   (2)

 

Where R ̇ is the velocity of the bubble wall, R ̈ is the acceleration of the bubble wall, s is the surface tension, µ is the viscosity coefficient for acetone, p₀ is atmospheric pressure, p_A(t+R/c) is the supersonic sound pressure as a function of time, t, c is the velocity of sound, p∞ is the atmospheric pressure, and p_B(R,t) is the liquid pressure at the bubble interface.

  Because the prototype small-scale UTPC equipment used a 0.1 mm nozzle, the radius of the water jet cavitation bubbles was smaller than that obtained using a larger 0.8 mm nozzle, which was approximately 100 μm Yoshimura et al. (2021b). However, because the UTPC apparatus incorporated a swivel nozzle attached to the water jet nozzle, the bubbles were enlarged compared with those obtained during MFC without a swivel nozzle Yoshimura et al. (2021c). Using the Keller-Miksis formulation, the changes in bubble radius and internal pressure and temperature in acetone were calculated for an initial bubble size of 10 μm, a sound pressure of 1 atm and a bubble contraction to 0.1 μm. As previously reported Yoshimura et al. (2018c), the shrinkage pressure associated with MFC equipped with a large 0.8 mm nozzle was 7.51 × 10⁷ MPa, while that during UTPC using a small 0.1 mm nozzle was determined to be 1.10 × 10⁵ MPa. In addition, the temperature at the time of shrinkage was 1.68 × 10¹² K for the large-scale equipment [Yoshimura et al. (2018c)] and 3.07 × 1012 K for the smaller apparatus, due to the higher expansion coefficient of the bubbles (3.75 = 37.5/10). In previous work Zoghi-Foumani and Sadighi-Bonabi (2014) with an initial bubble radius of 5.10 μm, the bubble internal temperatures were determined to be in the range of 10⁶ K < T < 10⁷ K. In reality, as the temperature inside the bubbles increases, the upper limit is determined by thermal decomposition of the deuterated acetone vapor, chemical reactions and thermal conductivity. The present calculations indicated that the temperature inside bubbles exceeded 1.0 × 10⁸ K, which is the value required for bubble fusion. However, both the large and small-scale equipment generated internal bubble pressures much smaller than the value of 1.0 × 1010 MPa required for fusion. To address this problem, it was determined that an energy other than the WJ and ultrasonic energy sources was required.

 

 

 

 

 

 

 

 

 

 

 

 

Figure 3 The (a) acoustic pressure, (b) bubble radius, (c) bubble internal pressure and (d) bubble internal temperature in acetone as functions of time for various processes

 

3.2 COLLISIONS BETWEEN BUBBLES DUE TO LORENTZ FORCE

The force between two charges q1 and q2 associated with charged bubbles is:

 

                                                                                           (3)

where e is the elementary charge (1.602 × 10^-19 C), and ε0 is the permittivity of a vacuum (8.854 × 10^-12 C/Vm). These two charges can be calculated as:

 

                                                                                                                          (4)

and

 

                                                                                                                                   (5)

 

where Mq¹ and Mq² are the moles of ions in the two charged bubbles.

The Lorentz force can then be approximated as:

 

                                                                                                        (6)

 

Where B is the magnetic flux density (T), and v is the flow velocity of the charged bubble. The cross product of these terms is:

 

                                                                                         (7)

 

The pressure inside a bubble having a radius of 10 μm (which is the initial radius calculated using the Keller-Miksis formulation) that collides with a charged bubble in conjunction with shrinkage to 0.1 μm was calculated. Based on a nozzle diameter of 0.1 mm and flow rate of 160 mL/min, the flow velocity at the nozzle outlet was determined to be 340 m/s if the outlet loss was ignored. Because the flow velocity decreased on leaving the nozzle discharge part, the Lorentz force was calculated using equation (6) with the flow velocity near the outlet set to 100 m/s. Although the number of charged ions obtained from a WJC process is less than that generated during MFC, it was assumed that the water vapour was thermally decomposed in the WJC bubbles to generate ions.

When the two neodymium magnets shown in Figure 1were placed in the lower part of the apparatus facing the nozzle, the magnetic force lines from the north to south poles of the magnets crossed the liquid injection direction near the nozzle outlet. The cross product (that is, the outer product) of the velocity, v, of the charged particles and the magnetic field, B, equalled the Lorentz force, F, based on Fleming's left-hand rule. The Lorentz force acted perpendicular to the direction in which the charged cavitation bubbles flowed such that the bubbles collided.

　It was assumed that the magnetic flux density was 100 mT near the WJ nozzle of the small-scale UTPC equipment and that charged bubbles would collide with uncharged bubbles due to the Lorentz force of the magnetic field during shrinkage. The relationship between the number of moles of charged ions in a charged bubble and the pressure of the bubble collision is shown in Figure 4. In the case that 0.001 moles of charged ions were present, the collision pressure would be expected to exceed the 1.0 × 10¹⁰ MPa required for bubble fusion. Further increasing the magnetic field would be expected to lower the number of moles of ions required to achieve the threshold pressure.

Figure 4 Bubble collision pressure during shrinkage as a function of the number of moles of charged ions in a bubble (flow velocity: 100 m/s)

 

The flow velocity decreases at the position at which the cavitation cloud grows. The threshold pressure at which the bubbles expand isothermally is the Blake threshold Atchley1989., and this value increases along with the cavitation flow velocity. Therefore, in the case that the bubble flow velocity decreases, the Blake threshold is also reduced such that a large number of MFC bubbles are generated and the bubble temperature rises. Consequently, the number of ions resulting from thermal decomposition in the bubbles increases. Figure 5 plots the relationship between the number of moles of charged ions in the bubbles and the bubble collision pressure due to the Lorentz force for a bubble flow velocity of 5.0 m/s at the Blake threshold pressure. In excess of 0.017 moles of charged ions were required in a charged bubble to exceed the threshold pressure of 1.0 × 10¹⁰ MPa. The formation of these ions was promoted by repeated isothermal expansion and adiabatic compression of bubbles during the UTPC process. Therefore, the reduction in collision pressure did not occur. Increasing the magnetic flux density above 100 mT caused the pressure to exceed the threshold value for bubble fusion even with a small number of ions in the bubble (Table 2). It should be noted that, in the case that a collision plate (a specimen for the surface modification of a material) is installed in the cavitation cloud, the flow direction changes when the cavitation cloud collides with the plate, which complicates the direction in which the Lorentz force acts

Figure 5 Bubble collision pressure during shrinkage as a function of the number of moles of ions in the bubbles (flow velocity: 5.0 m/s)

 

Table 2 Maximum internal pressures and temperatures of bubbles during UC and MFC in an acetone reaction furnace and required pressure and temperature values for the D-T fusion reaction

Footnote: D + T → 4He + n (14 MeV)

 

 

 

3.3 BUBBLE ENERGY DENSITY

The bubble spacing resulting from expansion, L, can be calculated as

 

                                                                                                                 (8)

 

Where Rmax/R0 is the bubble expansion rate and R0 is the initial bubble radius. The bubble movement due to expansion, Δr, can be calculated as:

 

                                                                                                                        (9)

 

Were r is the initial distance between q¹ and q².

The amount of work required to move charge q2 toward charge q1 by Δr is

 

                                                                                                               (10)

 

The increase in the energy density within each bubble, ΔE, is:

 

                                                                                                          (11)

 

The increase in energy density per atom, ΔE/atom can be calculated as:

 

                                                                                                                         (12)

Where NA is Avogadro’s number (mol-1; 6.022 × 1023).

In the case that a charge q² is moved by an electric field E(r) we have the energy density E_d:

 

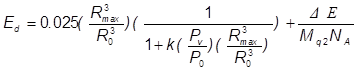                                                           (13)

Which can also be written as:

 

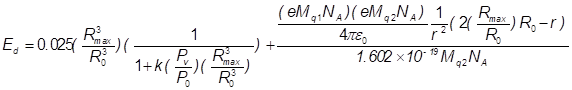 (14)

 

Where k is the fraction of vapour escaping condensation and Pv is the vapour pressure of the host liquid. A plot of Ed versus Rmax/Ro is presented in Figure 6. The fusion energy threshold is known to be 10⁴ eV per atom or molecule Arakeri (2003) and k was assigned a value of 0.025 based on the results of Storey and Szeri Storey and Szeri (2000). Using this value together with Pv/Po = 10^-5 (which is typical of fluids such as ethylene glycol; Po = 1 bar), it appears that the required energy density, Ed Arakeri (2003), can be obtained with an expansion ratio of approximately 75 Yoshimura et al. (2018c). Thus, assuming that the k value of acetone is relatively low, it should be possible to obtain the required energy density

If the proportion of steam escaping condensation in heavy acetone can be estimated, the enlargement ratio for bubbles exceeding the threshold can be obtained. The temperature at the time of bubble shrinkage calculated from equations (1) and (2), as shown in Figure 3, was assumed to be the number of vapor moles of the initial bubbles in the standard state. This quantity of moles also changed with the bubble volume. This is based on the assumption that the vapor in the bubble flows out of the bubble wall during expansion, and also flows out of the bubble wall in a manner similar to breathing during shrinkage. However, although the energy in the bubble increases, primarily due to changes in pressure and volume, if the amount of steam remaining in the bubble is too large, the temperature cannot be expected to rise Yoshimura et al. (2018c). Assuming that the number of moles in the bubble remains constant, the temperature during bubble contraction will not increase. In addition, the temperature will rise as the proportion of residual acetone that escapes evaporation, pyrolysis and condensation decreases Yoshimura et al. (2018c). In the case of acetone, Pv/Po = 0.242 and k = 1 × 10^-6. As shown in Figure 6, without the magnetic field, an Rmax/Ro greater than 77 allows Ed to exceed the threshold of 1 × 10⁴ eV/atom. Thus, in order to obtain a high value of Ed and realize bubble fusion, it is necessary to increase Rmax/Ro and to decrease k. Increasing the expansion rate of the heavy acetone bubbles thus necessitates further increases in the sound pressure.

The data in Figure 6 also show the relationship between the expansion coefficient and the energy density when the increase in energy density due to the expansion of UTPC bubbles in a strong magnetic field was incorporated based on using equation (14). Here, it is assumed that a bubble having a charge q¹ has an initial radius of 10 μm and is in contact with a bubble having a charge q², which has the same initial radius. Upon expanding in response to ultrasonic waves, the first bubble moves the second bubble and thus performs work. As an example, if both bubbles have an expansion factor of 1.5 with an inter-bubble distance of 30 μm, the movement amount is 10 μm to give a new inter-bubble distance of 20 μm. In the case that the expansion coefficient for the initial 10 μm bubble shown in Figure 3is 3.75, Ed becomes 1.19 × 10⁴ eV/atom, which exceeds the threshold value of 1.0 × 10⁴ eV/atom. These calculations suggest that it should be possible to realize bubble fusion based on a realistic ultrasonic sound pressure.

Figure 6 Bubble energy density versus expansion ratio for k = 1 × 10-6 and Pv/Po = 0.242. The dashed line shows the fusion threshold of 104 eV per atom or molecule

 

4. CONCLUSION

In order to carry out bubble fusion experimentally, the present work employed a prototype small-scale MFC apparatus to perform UTPC in association with a strong magnetic field. The following conclusions were obtained.

1)     When the WJC generated using a 0.1 mm nozzle via the small-scale equipment was combined with ultrasonication, the pressures and temperatures inside the bubbles during bubble shrinkage could be estimated using the Keller-Miksis equation.

2)     A strong magnetic field was applied near the outlet of the liquid jet nozzle to promote the generation of MFC bubbles. Because these bubbles contained charged species, they experienced a Lorentz force due to the magnetic field and underwent stronger collisions. The resulting bubble pressures exceeded the threshold value necessary for bubble fusion.

3)     The expansion of charged bubbles in response to changes in the sound pressure due to ultrasonic irradiation caused these bubbles to perform work on adjacent charged bubbles. As a consequence, the energy density of the atoms in the bubbles exceeded the threshold required for bubble fusion.

4)     The results of this work strongly suggest that ultra-high temperature and pressure cavitation within a strong magnetic field may cause bubble fusion.

 

Acknowledgement

This research was supported in part by a JSPS KAKENHI Grant-in-Aid for Scientific Research (C) (grant no. 19K04110).

 

 

REFERENCES

Arakeri H V. (2003) Sonoluminescence and bubble fusion. Current Science ; 85(7) : 911-916. Retrieved from https://www.jstor.org/stable/24108772

Atchley A. (1989) The Blake threshold of cavitation nucleus having a radius-dependent surface tension. J. Acoust. Soc. Am. ; 85(1) : 152-157. Retrieved from https://doi.org/10.1121/1.397724

Barber B P, Hiller R A, Ritva L S, Putterman J K, Weninger R. (1997) Defining the unknowns of sonoluminescence. Phys Rep. ; 281 : 65-143. Retrieved from https://doi.org/10.1016/S0370-1573(96)00050-6

Barber B P, Putterman S. (1991) Observation of synchronous picosecond sonoluminescence. Nature ; 352 : 318-320. Retrieved from https://doi.org/10.1038/352318a0

Gaitan D F, Crum Lawrence A, Church C C, Roy R A. (1992) Sonoluminescence and bubble dynamics for a single, stable, cavitation bubble. Journal of the Acoustical Society of America ; 91(6) : 3166-3183. Retrieved from https://doi.org/10.1121/1.402855

Gompf B, Gunther R, Nick G, Pecha R, Eisenmenger W. (1997) Resolving sonoluminescence pulse width with time-correlated single photon counting. Phys Rev Lett. ; 79 : 1405-1408. Retrieved from https://doi.org/10.1103/PhysRevLett.79.1405

Ijiri M, Yamaguchi K, Kikuchi S, Kato F, Kunieda Y, Sakurai H, Ogi T, Yoshimura T. (2021) Formation of a phosphoric acid compound film on an AZ31 magnesium alloy surface using cavitation bubbles. Surface and Interfaces ; 25 : 101194-1-11. Retrieved from https://doi.org/10.1016/j.surfin.2021.101194

Keller J B, Miksis M. (1980) Bubble oscillations of large amplitude. Journal of the Acoustical Society of America ; 68 (2) : 628-633. Retrieved from https://doi.org/10.1121/1.384720

Kling CL. (1970) A High speed photographic study of cavitation bubble collapse. University Michigan Report No. 03371-2-T : 08466-7-T. Retrieved fromhttps://apps.dtic.mil/sti/citations/AD0705375

Plesset M W. (1949) The dynamics of cavitation bubbles. Journal of Applied Mechanics: 16277-16282. Retrieved from https://doi.org/10.1115/1.4009975

Putterman S, Weninger K. (2000) Sonoluminescence : How bubbles turn sound into light. Ann Rev Fluid Mech. ; 32 : 445-476. Retrieved from https://doi.org/10.1146/annurev.fluid.32.1.445

Rayleigh L. (1917) On the pressure developed in a liquid during the collapse of a spherical cavity. Philosophical Magazine ; 34(200) : 94-98. Retrieved from https://doi.org/10.1080/14786440808635681

Seife C. (2002) Bubble Fusion Paper Generates A Tempest in a Beaker. Science ; 295 :1808-1809. Retrieved from https://doi.org/10.1126/science.295.5561.1808

Storey B D, Szeri A J. (2000) Water vapor sonoluminescence and sonochemistry. Proc. R. Soc. London Ser. A. ; 456 : 1685-1709. Retrieved from https://doi.org/10.1098/rspa.2000.0582

Summers D. (1987) Consideration in the design of a waterjet device for reclamation of missile casings. Proc of the 4th U.S. Water Jet Conference, The University of California, Berkeley : 82-89. Retrieved from https://scholarsmine.mst.edu/min_nuceng_facwork/157/

Taleyarkhan R P, West C D, Cho J S, Lahey R T, Nigmatulin Jr R, Block R C. (2002) Evidence for Nuclear Emissions During Acoustic Cavitation. (Http : //www.sciencemag.org/feature/data/hottopics/bubble/index.shtml), Science ; 295 : 1868 -1873. Retrieved from https://doi.org/10.1126/science.1067589

Yoshimura T, Iwamoto M, Ogi T, Kato F, Ijiri M, Kikuchi S. (2021a) Peening Natural Aging of Aluminum Alloy by Ultra-High-Temperature and High-Pressure Cavitation. Applied Sciences ; 11(2894) : 1-13. Retrieved from https://doi.org/10.3390/app11072894

Yoshimura T, Nishijima N, Hashimoto D, Ijiri M. (2021c) Sonoluminescence from ultra-high temperature and pressure cavitation produced by a narrow water jet. Heliyon; 7(8) E07767:1-8. Retrieved from https://doi.org/10.1016/j.heliyon.2021.e07767

Yoshimura T, Shimonishi D, Hashimoto D, Nishijima N, Ijiri M. (2021b) Effect of Processing Degree and Nozzle Diameter on Multifunction Cavitation. Surface Engineering and Applied Electrochemistry ; 57(1) : 101-106. Retrieved from https://doi.org/10.3103/S1068375521010154

Yoshimura T, Tanaka K, Ijiri M. (2018b) Nanolevel surface processing of fine particles by waterjet cavitation and multifunction cavitation to improve the photocatalytic properties of titanium oxide. IntechOpen Cavitation doi: 10.5772/intechopen.79530, IntechOpen Limited, 5 Princes Gate Court, London, SW7 2QJ, UK. Retrieved from https://doi.org/10.5772/intechopen.79530

Yoshimura T, Tanaka K, Yoshinaga, N. (2018a) Nano-level Material Processing by Multifunction Cavitation. Nanoscience & Nanotechnology-Asia ; 8(1) : 41-54. Retrieved from https://doi.org/10.2174/2210681206666160922164202

Yoshimura T, Yoshiya H, Tanaka K, Ijiri M. (2018c) Estimation of Bubble Fusion Requirements during High-Pressure, High-Temperature Cavitation. Int J Adv Technol. : doi :10.4172/0976-4860.1000206 Retrieved from https://doi.org/10.4172/0976-4860.1000206

Young J B, Schmiedel, T, Kang W. (1996) Sonoluminescence in High Magnetic Fields. Phys Rev Lett. ; 77(23) : 4816-4819. Retrieved from https://doi.org/10.1103/PhysRevLett.77.4816

Zoghi-Foumani N, Sadighi-Bonabi R. (2014) Investigating the possibility of Sonofusion in Deuterated acetone. International Journal of Hydrogen Energy ; 39 (21) : 11328-11335 Retrieved from https://doi.org/10.1016/j.ijhydene.2014.04.084