On some comparison the methods of Runge-Kutta and Multi-step types

 

A.R. Abdulkarimova ¹

 

¹ Administrative Assistant, Landau School Local, Azerbaijan

 

1. INTRODUCTION

Scientists have been investigating the solution of initial-value problems for Ordinary Differential Equations since the Age of Newton. To find a numerical solution to the above-named problem, the specialists mainly have used power series.

Leonard Euler has shown the main disadvantage of such methods and proposed his direct numerical method, which is successfully used at present. In scientific literature, this method is called the direct numerical method for solving the initial value problem for the Ordinary Differential Equation of the first order, which can be presented as follows:

 

 

Suppose that problem (1) has the unit continuous solution defined in the segment, where has the continuous derivatives up to, inclusively. And the continuous to totality of arguments function  has defined in some closed set, where has the partial derivatives up to some, inclusively. For finding a numerical solution of the problem (1) in usually, the segment  is divided into N-equal parts by using a constant step size  and the mesh points define as. Let us by the  define the exact values of the solution of problem (1) at the point, but the corresponding approximate value has defined as the

The Euler method was developed by Adams, Runge, Kutta, and Akad. Kyrilov, Dahlquist, Bakhvalov, and other known scientists. In the results of which appeared the class methods as the one-step and Multi-step methods. The last time constructed the new class methods were hybrid, advanced, predictor-corrector, and so on. Fundamental research into numerical methods began in the middle of the last century. The number of papers devoted to the study of those numerical methods increased.  There was a need to compare them. For this aim proposed to use the conception of stability and degree. To obtain more reliable results, it appeared necessary to construct A or R- stable. Some authors suggested using L-stable methods.

There was a need to construct new methods. For the illustration of this, let us consider the following multistep methods (see for example Ibrahimov & Imanova (2021), Ibrahimov (1990), Imanova & Ibrahimov (2023), Ibrahimov (1984), Juraev et al. (2023), Ibrahimov & Imanova (2024), Ibrahimov & Imanova (2024), Brunner (1984), Trifunov (2020), Dahlquist (1956), Akinfewa et al. (2011), Butcher (1965), Urabe (1970), Gupta (1979), Bakhvalov (1955), Shura-Bura (1952), Dahlquist (1959), Skvortsov (2009), Kobza (1975), Dahlquist (1956)):

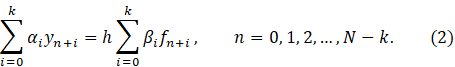
The explicit Runge-Kutta method In one version can be presented as follows

 

 Here, the functions  define as the following:

.

As it follows from the definition of the function of , method (3) is explicit. Let us the functions  to define as follows:

.

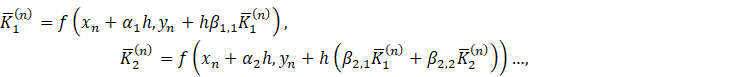
Let us consider the following method:

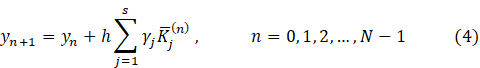
By simple comparison methods (3) and (4), receive that method (3) is explicit and method (4) is implicit. Noted that method (2) is explicit in the case  and method (4) is explicit in the case  for the .

It is easy to understand that application of the Runge-Kutta method is more difficult. However, these methods have an extended region of stability. Some experts approve the claim that someone can construct a specific method, the panels by using that applied that to solve some applied problems. It should be noted that recently there has been a frequent necessity to construct new methods with new properties. Therefore the construction of new methods with new properties is always relevant. As is known, the application of one-step methods to solve some practical problems performed very simply. However, this is not always the case. For example, in using method (4) for calculating the values to each  is difficult. Note that the application of the method (3) is easier than a method (4). With similar cases collide in using the Multi-step methods.

And now let us establish some connections between one-step and multi-step methods. For this consider the following method:

which is received from the method (2) for the value . In the formula (5) let us to change  by the , then receive the following method.

Which usually is called the Midpoint rule. Now let us define the relation between the methods (2), and with Runge-Kutta methods. For this aim, consider the following method:

here  and .

Note that methods (6) and (7) have the same degree .

Let us consider the trapezoidal rule, which can be presented as follows:

This method has the degree  and is implicit, therefore this can be received from the method (2) in the case  . Method (8) can be received from the method (4) in the case . In this case the functions, can be constructed as the following:

By using these in formula (8), receive:

This method is called the Heun’s method.

Let us consider the following presentation of the Taylor series:

.

After using this in the formula (9) one can be writte:

From here by discarding the reminder term, receive:

which is the Trapezoidal rule. Thus, some connections were established between the one-step and multi-step methods. It is obvious that by selecting some unknowns in method (3) one can receive some known and unknown methods. By using the above-described schemes, let us consider obtaining methods of (2) from the method (3).

1)    About some connection between Multistep methods and Methods Runge-Kutta.

For the illustration relation between Multistep and Runge-Kutta methods, let us consider the following Runge-Kutta method with the fourth order:

here

Let us consider the following equality

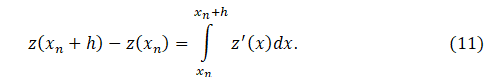
If applied equality (11) the following initial-value problem

then receive:

And now, let us in the method (2) to put . In this case stable method with the degree , can be presented as follows:

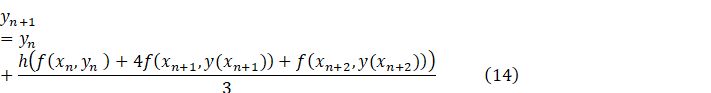
This is well known Simpson method, which has been received from method (2) as partial case. By simple comparison of the methods (10) and (14), receive that if in the method (13) select  as , then from the method (13) it follows method (14) and to contrary, if in the method of (14) step-size  select as , then from the method (14) follows method (10).

And now let us consider the case . Then by choosing the unknowns  as the  and , then from the method (3) it follows Midpoint rule (formula (7)). If to consider the case  and , then from the method (3) one can be received the Heun’s method.

Noted that in the case  one can construct a method, which is different from the above noted methods:

here

Let us consider construction method of type (4). For the simplicity to consider the following method,

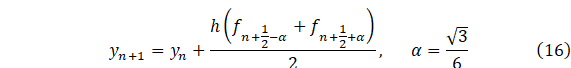
which formally be obtained from the method (4) as a partial case. All the unknowns that participated in the (4) must receive the value of rational type. But in the method (16) participate irrational quantity α. Therefore, this method doesn’t belong to a class of method (4)

Let us consider the following method:

If in the method of (17) to use Euler explicit method

then methods (15) and (17) will be  same.

As is known, the Runge-Kutta methods are stable. But in a class of Multistep methods, not all methods are stable. As is known in the comparison of Numerical methods, the conception of stability and degree. Therefore let us consider definitions of conception stability and degree for the method (2).

Definition 1. Method (2) is called stable, if the roots of the polynomial

located in the unit circle, on the boundary of which there are not multiple roots.

Definition 2. The integer value  is called as the degree for the method (2) if the following is holds:

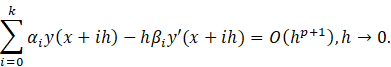
Definition 3. The integer value s is called as the order of the method (3) or (4) if the function:

has the following property:

By using this definition, receive those methods (5), (6)  and has the degree , method (7) has the order . Method (10) has the order  and methods (13) and (14) have the degree . Noted that method (15) has the order , methods (14) and (16) have the degree .

 

 

 

2. Conclusion

As is known in solving many applied problems, arises the question about the selection of numerical methods for solving the above-investigated problems. Many experts in such cases suggested using the methods of Runge-Kutta and Adams, Considering that these methods are very popular and simple to use. However, such tasks have arisen in solving which above recommended methods have not given available results. Taking into account the stated fact, experts suggested using the generalization of these methods. In the results of which arises the Multistep methods with constant coefficients and semi-implicit Runge-Kutta methods. Recently, new directions have appeared which are called the implicit Runge-Kutta methods. For simplicity here, suggest investigating above named methods. The main advantage of this research is the comparison of one-step and multistep methods and shown that how one can be received. As is known, the region of stability for the Runge-Kutta methods is wider than the region of stability for the multistep methods. For the sake of objectivity, let us note that the region of stability can be extended by using predictor-corrector methods. Assume that the method described here is promising, therefore the results received here will find its followers.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Akinfewa, O. A., Yao, N. M., & Jator, S. N. (2011). Implicit Two-Step Continuous Hybrid Block Methods with Four Off-Step Points for Solving Stiff Ordinary Differential Equations. World Academy of Science, Engineering and Technology, 51, 425-428.

Bakhvalov, N. S. (1955). Some Remarks on the Question of Numerical Integration of Differential Equations by the Finite-Difference Method. Academy of Science Report, USSR, 3, 805-808.

Brunner, H. (1984). Implicit Runge-Kutta Methods of Optimal Order for Volterra Integro-Differential Equations. Mathematics of Computation, 42, 95-109. https://doi.org/10.1090/S0025-5718-1984-0725986-6

Butcher, J. C. (1965). A Modified Multistep Method for the Numerical Integration of Ordinary Differential Equations. Journal of the Association for Computing Machinery, 12, 124-135. https://doi.org/10.1145/321250.321261

Dahlquist, G. (1956). Convergence and Stability in the Numerical Integration of ODEs. Mathematica Scandinavica, 4, 33-53. https://doi.org/10.7146/math.scand.a-10454

Dahlquist, G. (1959). Stability and Error Bounds in the Numerical Integration of Ordinary Differential Equations. Transactions of the Royal Institute of Technology, Stockholm, Sweden, 130, 3-87.

Gupta, G. K. (1979). A Polynomial Representation of Hybrid Methods for Solving Ordinary Differential Equations. Mathematics of Computation, 33, 1251-1256. https://doi.org/10.1090/S0025-5718-1979-0537968-6

Ibrahimov, V. R. (1984). Relationship between the Order and the Degree for a Stable Forward-Jumping Formula. Prib. Operator Methods. Urav. Baku, 55-63.

Ibrahimov, V. R. (1990). A Relationship Between Order And Degree for a Stable Formula with Advanced Nodes. Computational Mathematics and Mathematical Physics (USSR, 30), 1045-1056. https://doi.org/10.1016/0041-5553(90)90044-S

Ibrahimov, V., & Imanova, M. (2021). Multistep Methods of the Hybrid Type and Their Application to Solve the Second Kind Volterra Integral Equation. Symmetry, 13(6), 1-23. https://doi.org/10.3390/sym13061087

Ibrahimov, V., & Imanova, M. (2024). About One Multistep Multiderivative Method of Predictor-Corrector Type Constructed for Solving Initial-Value Problem for ODE of Second Order. WSEAS Transactions on Mathematics, 599-607. https://doi.org/10.37394/23206.2024.23.63

Ibrahimov, V., & Imanova, M. (2024). On Some Ways to Increase the Exactness of the Calculating Values of the Required Solutions for Some Mathematical Problems. WSEAS Transactions on Mathematics, 430-437. https://doi.org/10.37394/23206.2024.23.45

Imanova, M. N., & Ibrahimov, V. R. (2023). The Application of Hybrid Methods to Solve Some Problems of Mathematical Biology. American Journal of Biomedical Science and Research, 18(6), 74-80. https://doi.org/10.34297/AJBSR

Juraev, D., Ibrahimov, V., & Agarwal, P. (2023). Regularization of the Cauchy Problem for Matrix Factorizations of the Helmholtz Equation on a Two-Dimensional Bounded Domain. Palestine Journal of Mathematics, 381-402.

Kobza, J. (1975). Second Derivative Methods of Adams Type. Applikace Mathematicky, 20, 389-405. https://doi.org/10.21136/AM.1975.103607

Shura-Bura, M. R. (1952). Error Estimates for Numerical Integration of Ordinary Differential Equations. Prikladnaya Matematika i Mekhanika, 5, 575-588.

Skvortsov, L. (2009). Explicit Two-Step Runge-Kutta Methods. Mathematical Modeling, 21, 54-65.

Trifunov, Z. (2020). Definite Integral for Calculating Volume of Revolution That is Generated by Revolving the Region about the X(Y)-Axis and Their Visualization. Educational Alternatives, 18, 178-186.

Urabe, M. (1970). An Implicit One-Step Method of High-Order Accuracy for the Numerical Integrations of ODE. Numerische Mathematik, 2, 151-164. https://doi.org/10.1007/BF02165379