A FUZZY-SOFT-SET THEORYAPPROACH FOR SOLVING DECISION-MAKING PROBLEMS ON CERTAIN HYBRID SET MODEL

 

Shamshad Husain ¹, Vipin Kumar Tyagi ², Mridul Kumar Gupta ³

 

^{1, 2} SBAS, Shobhit Institute of Engineering and Technology, Deemed to be University, Meerut, U.P., India

² Department of Mathematics, C.C.S. University, Meerut, 250001, U.P., India

 

1. INTRODUCTION

Zadeh (1965) was the first to define a fuzzy set as a category of objects having a whole lot of club grades. This series is defined through a membership (characteristic) characteristic that assigns each item a club grade between 0 and one. Molodtsov (1999), who additionally gave the idea's early discoveries, proposed the principle of soft sets' core ideas. Maji et al. (2002) used the concept of soft units to a selection-making problem with the use of fundamental arithmetic. Roy & Maji (2007) observed an approach to the problem of creating decisions in an uncertain scenario. Shaky multi-observer facts set from a cutting-edge item reputation method become displayed by way of them. The system involved constructing a Comparison table out of a fuzzy-soft-set that allows you to make judgments.  The algorithm for item identity, as proven via a counter-instance, changed into no longer the ultimate preference, in step with Kong et al. (2009), and it cannot be attained commonly. Presented the case that the selection value now not have capabilities to answer choice-making concerns with fuzzy soft units for you to give a greater thorough knowledge of choice-making primarily based on fuzzy-soft-sets. Çağman, & Karataş (2013) defined the intuitionistic fuzzy-soft-set principle and solved a number of unsure actual-international decision-making issues. Yang et al. (2013) created the idea of multi-fuzzy soft units related to the multi-fuzzy set and soft set ideas. They then used it to choose-making. Husain & Shivani (2018)'s theoretical paintings of the soft set become built upon De Morgan's regulation (with evidence and other legal guidelines of the universe Jana & Pal (2018) paired bipolar intuitionistic fuzzy soft units with a soft set to address selection-making concerns. Khalil et al. (2019) described a unique soft set known as an inverse fuzzy soft set, in conjunction with its traits, functions, and operations.  Decision-making problems have been applied to reveal the applicability of the technique. Riaz & Tehrim (2019) developed a mathematical model in which bipolarity is treatable, and precisely locate the disorder of bipolar fuzzy-soft-set (BFS-set) and its mappings. In order to provide excellent diagnostic and therapy recommendations, BFS mappings have been additionally made available. Begam et al. (2020) determined a similarity metric for lattice-ordered multi-fuzzy-soft-sets using the set-theoretic method and its software in selection-making. A novel software of soft set concept in selection-making below uncertainty turned into made by using Dalkılıç et al. (2021). Zulqarnain et al. (2021) determined the correlation coefficient by the TOPSIS technique primarily and used for selection-making. Akram et al. (2022) employed selection-making strategies based totally on fuzzy soft opposition hypergraphs. We created fuzzy soft hypergraphs, a singular framework that exports the features of fuzzy-soft-sets to hypergraphs. In a trapezoidal interval kind-2 fuzzy (TrIT2F) setting, the high-quality-worst technique (BWM) and statistics envelopment evaluation (DEA) are blended. For the purpose of selecting a temporary health center, Chen et al. (2022) checked out a performance-based multi-standards organization selection-making (MCGDM) method. The generalizability of the proposed structure is investigated in comparison to the relevant pre-existing fashions and the encouraged similarity system by Rahman et al. (2022). To position up an assessment table for better-level cognitive competencies. The advised method is given to resolve desire-related troubles, and extensively fuzzy-soft-set decision problems and a variety of opportunities will be taken into account earlierin choosing one correct parametric value by Husain et al. (2022).  Husain et al. (2022) used a family of linked subsets to create a club characteristic for fuzzy soft units. Additionally, they produced a hybrid model for a single decision maker to choose a choice value. They supplied a logo-new approach that permits the use of fuzzy-soft-sets in organization deliberation. As an inexperienced issuer, Reema et al. (2023) discovered and decided on the high-quality inexperienced and sustainable dealer, considering inexperienced technologies, inexperienced merchandise, green packaging, etc.

The article is organized as follows: In Section 2, we go over some vital ideas referring to soft units. Section 3 will cover tough units and fuzzy-soft-sets. We provide a technique for making choices based totally on certain hybrid soft-set models. Section 4 specializes in weighted fuzzy-soft-set ideas in choice making and soft-set primarily based selections.

 

 

2. MATERIALS AND METHODS

Definition 2.1 [Roy & Maji (2007)]: Let U be the regularly occurring set of factors and E be the set of parameters. Paired set (U, E) seems like a soft universe. Let A be the subset of E and (F, A) is denoted a soft set over the soft universe (U, E), where F: A→P(U).

Definition 2.2: A soft multi-set over (U, E) is denoted by (M, A), wherein A⊆E and described as M: A→P(U). Every soft multi-set M(A) may be described with accomplice parametric family of count number features as: where  and  is a characteristic family of multi soft set of M (a), which is a sub set of U.

Definition 2.3: Let I^U be the set of all fuzzy subsets of initial universe set U. Let A⊆E, a set of parameters, then the pair (F, E) is known as a fuzzy-soft-set over U, wherein 

Definition 2.4: For every a ∈ E and x ∈ U, the union of two fuzzy-soft-set (F, E) and (G, E)is a fuzzy-soft-set (H,E), is given by .

Definition 2.5: For every a ∈ E and x ∈ U, the intersection of two fuzzy-soft-set (F,E) and (G,E) is the fuzzy-soft-set and is given by .

Definition 2.6 [Shabir et al. (2013)]: Let(F,E) be afuzzy-soft-subset of the fuzzy-soft-seti.e and  where membership is defined as

Definition 2.7: The fuzzy-soft-set (F, E) is said to be equal to (G, E), i.e , if   and .

Definition 2.8: The complement (H, E) of (G, E) in (F, E) is defined as

 

 and .

 

Definition 2.9: Let X be a fuzzy set over a parametric set E over a universe set U with membership function . A fuzzy parameterized fuzzy-soft-set τ_x over U is defined by a function γ_x (x), where s.t. , if . A fuzzy parameterized fuzzy-soft-set (fpfs-set) over U is an ordered paired set defined as:

 

.

 

The set of all fpfs-sets is denoted by FPFS(U).

Definition 2.10 [Ma et al. (2017)]: Let (U, R) be an approximation space, where R is an equivalence relation over universe U. A rough set X⊆U is definable, if or, where  and .

 

3. A HYBRID SOFT SET MODEL FORDECISION-MAKING 

Numerous applications of soft-set theory, operation studies, probability idea, and other theories were furnished by Molodtsov (1999), despite the fact that the approach provided in that take a look at has sure flaws. The algorithm beneath demonstrates how selection makers can pick the excellent choice to buy the product:

Algorithm 3.1:

Step 1: Find the soft set (F, E) and represents in the tabular form.

Step 2: Assign the priority P to each object (customer) for every set of desire parameter by the decision-maker, that is a subset of E.

Step 3: Evaluate all reduct-soft-sets (F, P) to the corresponding parametric values for getting the choice values (CV) of reduct-parameters.

Step 4: Calculate weighted reduct-soft-set (F, Q) [say] of (F, P), based on the weightage and obtain the weighted choice value of an object by

 

.

 

Step 5: Construct the weighted table for the soft set (F, Q) to determine WCV for optimal solution.

Step 6: Find k from the evaluation table, where, to identify the item having highest value (price) according to WCV.

Here, sometimes we get more than one choice value that is the same in the WCV table. In this situation, a decision maker has the choice to choose the optimal choice as per his parametric requirement.

Example 3.1: Let  be set of six nail polishes and  (quick to dry),  (lasting shiny appearance),  (cheap),  (durable),  (texture of color),  (display)} be the set of parameters.

Step 1: Consider soft set (F, E) which describes the attractiveness of the nail polishes given in the following Table 1:

Table 1    

Table 1 Soft-Set (F, E)
	1	1	1	0	1	0
	1	0	0	1	1	1
	1	1	0	1	1	1
	1	1	0	0	1	1
	1	0	0	0	1	1
	1	1	1	0	1	0

 

Step 2: In Table 1, we see  and  are two reducts of parameter set . Let us choose any one as . On this basis, Table 2 represents a reduct-soft-set as follows:

Step 3:

Table 2    

Table 2 Reduct–Soft-Set (F, P)
	1	1	1	0	1	0
	1	0	0	1	1	1
	1	1	0	1	1	1
	1	1	0	0	1	1
	1	0	0	0	1	1
	5	3	1	2	5	4

 

Step 4: Weighted choice value (WCV) of an object u ∈ U is , given by

 

.

 

Let decision-maker sets weight for parameters of Q as follows:

For the parameter , for the parameter , for the parameter ,

For the parameter , for the parameter .

Then, we can get the weighted table as follows:

Step 5:

  Table 3

Table 3 Weighted Table of Soft Set (F, Q)
	0.7	0.7	0.7	0.0	0.7	0.0
	0.2	0.0	0.0	0.2	0.2	0.2
	0.6	0.6	0.0	0.6	0.6	0.6
	0.5	0.5	0.0	0.0	0.5	0.5
	0.9	0.0	0.0	0.0	0.9	0.9
	2.9	1.8	0.7	0.8	2.9	2.2

 

Step 6: The decision maker will take the decision out of nail polish or according to her parametric choice P.

Now we extend the algorithm 3.1 for three fuzzy-soft-sets in algorithm 3.2 as follows:

 

Algorithm 3.2:

Step 1: Find the fuzzy-soft-sets (F, A), (G, B) and (H, C) and represents in the tabular form.

Step 2: Assign the priority P to each object (customer) for every set of desire parameter by the decision-maker, that is a subset of E.

Step 3: Evaluate the resultant-fuzzy-soft-set (K, R) from fuzzy-soft-sets (F, A) & (G, B) by operating into tabular form.

Step 4: Evaluate the resultant-fuzzy-soft-set (S, P) from fuzzy-soft-sets  by operating {} into tabular form.

Step 5: Construct the comparison table of the resultant-fuzzy-soft-set (S, P) and compute row-sum and column-sum for .

Step 6: When we have more than one choice value/optimal value is the same, construct the reduct comparison table of resultant-fuzzy-soft-set (S, P)

Step 7: Evaluate score-sum value  in the reduct comparison table of resultant-fuzzy-soft-set (S, P).

Step 8: Identify the item having highest value (cost) according to score-sum value in the reduct comparison table and the corresponding object is the best choice of the decision-maker.

Here, we illustrate the algorithm 3.2 with example 3.2:

Example 3.2: Let be set of six nail polishes havingdifferent colors, textures and shine. Theparameter set is as follows:

 

 

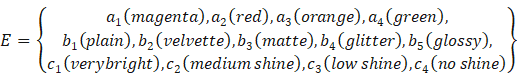
Let A, B, C denote three subsets of the set of parameter E according to color, texture and shine of nail polish respectively i.e. , , .

Mrs. X wants to buy a nail polish on the basis of “Attractiveness of nail polishes”.

Step 1: The fuzzy-soft-sets (F, A), (G, B) and (H, C) represent in the tabular form as Table 4:

Table 4    

Table 4 Fuzzy-soft-sets (F, A), (G, B) and (H, C)
Fuzzy-soft-set (F, A)
	0.3	0.1	0.7	0.5	0.1	0.1
	0.2	0.9	0.4	0.2	0.8	0.9
	0.4	0.6	0.3	0.5	0.2	0.4
	0.5	0.8	0.2	0.4	0.4	0.7
Fuzzy-soft-set (G, B)
	0.5	0.3	0.9	0.3	0.4	0.5
	0.5	0.4	0.8	0.4	0.3	0.5
	0.7	0.5	0.3	0.7	0.7	0.6
	0.6	0.6	0.5	0.5	0.4	0.5
	0.4	0.7	0.7	0.4	0.5	0.6
Fuzzy-soft-set (H, C)
	0.7	0.1	0.3	0.5	0.9	0.8
	0.6	0.5	0.1	0.6	0.9	0.1
	0.2	0.3	0.6	0.2	0.1	0.2
	0.3	0.2	0.7	0.4	0.1	0.7

 

Step 3: Perform (F, A)"AND" (G, B) to construct resultant-fuzzy-soft-set (K, R), we have 4×5=20 parameters of the form , where , for all ;  as Table 5:

 

Table 5

Table 5 Resultant-Fuzzy-Soft-Set (K, R)
	0.3	0.1	0.7	0.3	0.1	0.1
	0.3	0.1	0.7	0.4	0.1	0.1
	0.2	0.3	0.4	0.2	0.4	0.5
	0.2	0.5	0.3	0.2	0.7	0.6
	0.4	0.4	0.3	0.4	0.2	0.4
	0.4	0.6	0.3	0.5	0.2	0.4
	0.4	0.7	0.2	0.4	0.4	0.6

 

Step 4: The tabular representation of resultant-fuzzy-soft-set (S, P) will be as follows:

Suppose is the set of choice parameters of an observer. Then we have to take the decision from the availability set U.

Table 6    

Table 6 Resultant-Fuzzy-Soft-Set (S, P)
	0.3	0.1	0.3	0.3	0.1	0.1
	0.3	0.1	0.7	0.4	0.1	0.1
	0.2	0.3	0.1	0.2	0.4	0.1
	0.2	0.3	0.3	0.2	0.1	0.2
	0.3	0.2	0.3	0.4	0.1	0.4
	0.2	0.3	0.3	0.2	0.1	0.2
e45^c2	0.4	0.5	0.1	0.4	0.4	0.1
	1.9	1.8	2.1	2.1	1.3	1.2

 

Step 5: Construct the comparison table of the resultant-fuzzy-soft-set (S, P) and compute row-sum and column-sum for .

  Table 7

Table 7 Comparison Table of Fuzzy-Soft-Set (S, P)
	7	3	4	5	6	6	31
	4	7	4	4	6	6	31
	5	5	7	4	5	6	32
	7	3	4	7	6	7	34
	2	3	2	2	7	4	20
	3	3	3	3	5	7	24
	28	24	24	25	35	36

 

Step 6: When we have more than one choice value/optimal value is the same, construct the reduct comparison table of resultant-fuzzy-soft-set (S, P)

Step 7: Evaluate score-sum value in the reduct comparison table of resultant-fuzzy-soft-set (S, P).

Here, = row – sum of Table 7,  = column – sum of Table 7,

and   obtain = − as shown in Table 8:

  Table 8

Table 8 Reduct Comparison Table of Fuzzy-Soft-Set (S, P)
	31	31	32	34	20	24
	28	24	24	25	35	36
	3	7	8	9	−15	−12

 

Step 8: Here, from Table 8, the maximum score is 9, scored by and hence decision is in favour of selecting nail polish.

Now, we present an algorithm 3.3 for three fuzzy-soft-sets in which the first three steps are same as algorithm 3.2 as follows:

 

Algorithm 3.3

Step 1: Find the fuzzy-soft-sets (F, A), (G, B) and (H, C) and represents in the tabular form.

Step 2: Assign the priority P to each object (customer) for every set of desire parameter by the decision-maker, that is a subset of E.

Step 3: Evaluate the resultant-fuzzy-soft-set (K, R) from fuzzy-soft-sets (F, A) & (G, B) by operating {(F, A) AND (G, B)} into tabular form.

Step 4: Construct the Comparison table fuzzy-soft-set (S, P) and compute for . Here, and should be redesigned as

 

 and ,

 

whereis the membership cost of item for the k^th parameter and m is the variety of parameters

Step 5: The object having highest value (price) in the score-column is to be selected on the decision is k, if .

Now, we apply the algorithm 3.3 on example 3.2 as follows:

Construct the comparison table with reduct values of fuzzy-soft-setin Table –3.9 as follows:

  Table 9

Table 9 Comparison Table with Reduct Values of Fuzzy-Soft-Set
	0	0.1	−0.2	−0.2	0.6	0.7	1	2
	−0.1	0	−0.3	−0.3	0.5	0.6	0.4	3
	0.2	0.3	0	0	0.8	0.9	2.2	1
	0.2	0.3	0	0	0.8	0.9	2.2	1
	−0.6	−0.5	−0.8	−0.8	0	0.1	−2.6	4
	−0.7	−0.6	−0.9	−0.9	−0.1	0	−3.2	5

 

This is skew- symmetric matrix. The maximum score is obtained by or . Thus, the optimal choice for nail polish or  .

 

4. WEIGHTED FUZZY-SOFT-SET THEORY IN DECISION MAKING

In this section, presents a weighted fuzzy-soft-sets approach in the adjustable manner on the decision-making problems.

Definition 4.1 [Ma et al. (2017)]: Let σ = (F ̃, A) be a fuzzy-soft-set over U, where A ⊆ E and Eis the parameter set. The membership value soft ∈ [0,1], the t-level soft set of the fuzzy-soft-set σ is a crisp soft set defined as

for all .

Now, we present an algorithm 4.1 for weighted fuzzy-soft-sets as follows:

 

Algorithm 4.1:

Step 1: Find the fuzzy-soft-set σ = (F ̃, A) and represents in the tabular form.

Step 2: Multiply the priority values with corresponding resultant-fuzzy-soft-set and compute λ: A → [0, 1] for decision making.

Step 3:  Construct the table of the level soft set L (σ; λ) between σ and λ.

Step 4: Compute the weighted choice value of each object , where .

Step 5:  Compute the column-sum for each column in the WCV table to get optimal score.

Here, we illustrate the algorithm 4.1 with example 4.1:

Example 4.1: Let be set of six nail polishes and E= { (Quick to dry),  (lasting shiny appearance),  (cheap),  (durable),  (texture of color),  (display)} be the set of parameters.

Let consists of parameters that the decision maker is interested in buying a nail polish which qualifies with attributes in A to the utmost parameter.

Step 1: The tabular illustration of the fuzzy-soft-set σ = (F, A) describing “attractiveness of nail polishes” that the decision maker goes to buy is shown in Table 10:

Table 10  

Table 10 Fuzzy-Soft-Set Σ
	0.5	0.3	0.8	0.2	0.6	0.7
	0.4	0.6	0.2	0.3	0.3	0.6
	0.6	0.7	0.5	0.8	0.7	0.4
	0.7	0.7	0.4	0.5	0.5	0.3

 

Step 2: Let us take t = 0.6, then 0.6-level sets of fuzzy sets are

;;};

.

The tabular representation of the Level-soft-set L(σ;0.6) as follows:

Table 11

Table 11 Level Soft Set L (σ; 0.6)
	0	0	1	0	1	1
	0	1	0	0	0	1
	1	1	0	1	1	0
	2	3	1	1	2	2

 

Step 3: From the Table 11, we can see that is maximal. Thus, is the optimal choice object.

Now, if decision maker is given weights for parameters in A as follows:

For the parameter;for the parameter; for the parameter; for the parameter.

We have to apply weight function W: A → [0, 1] and the fuzzy-soft-set σ= (F ̃, A) is changed into a weighted fuzzy soft set.

Step 4: The tabular representation weight fuzzy-soft-set σ= (F ̃, A) is shown in Table 12:

Table 12  

Table 12 Weight Fuzzy-Soft-Set Σ
	0.0	0.0	0.5	0.0	0.5	0.5
	0.0	0.4	0.0	0.0	0.0	0.4
	0.7	0.7	0.0	0.7	0.7	0.0
	0.3	0.3	0.0	0.0	0.0	0.0
	1.0	1.4	0.5	0.7	1.2	0.9

          

Step 4: With the weighted approach in adjustable manner, is the maximal value in the given hybrid soft set model, Thus, is the optimal choice object.

 

5. COMPARATIVE ANALYSIS

In this section, we make an analysis of the research work that was taken into consideration are provided in response to the suggested research questions. The discussion is made on the basis of the comparative evaluation of the research questions as shown in Table 13.

Table 13

Table 13 Comparative Study
Authors	Year	Results and discussion
Ma et al. (2017).	2010	They described the use of weighted fuzzy-soft-set and provided a technique for solving the rough soft-setsselection-making problem. We advise distinct sorts of choice-making techniques. The nearest and most consultant cosmic components are discovered as a result of these instances.
Riaz et al. (2019)	2019	They identified bipolar fuzzy-soft-set (BFS-set) and BFS-mappings with mathematical modeling in disorder conditions.BFS mappings were also given the remedies for the first-class diagnosis.
Dalkılıç, (2021)	2021	He applied soft set theoryon MCDM problems with uncertainties. We provided an algorithm for MCDM problems and compared the results with existing findings.
Chen et al. (2022)	2022	They investigated an efficiency based MCGDM approach for makeshift selection of medical emergencies. With our work, fuzzy-soft-set can also be used in theadvised problems and successfullyresolve the challenges related to choice-making.

 

6. IMPORTANCE OF THE RESULT

Feng et al. (2010) provided the technique for object assessment and choice of a group by using Feng-soft, rough sets. In limited conditions, they found that the approach is applicable on Feng-soft, rough set that have to be a full soft set. Shabir et al. (2013) proposed a novel approach for soft, rough set (MSR-set) with limited restrictions in which Feng-soft, rough sets are eliminated from full soft sets and employing soft, rough sets can help with difficult choice-making. We proposed a completely unique approach to the MSR-set-based organization choice-making hassle. In this study, we discuss the usage of weighted fuzzy-soft-sets. In addition to that, we adapted a technique to solve a fuzzy-soft-set decision-making problem with insufficient data in real-world situations.  We develop two distinctive types of selection-making techniques for rough, soft sets. Under these circumstances, the nearest and optimal cosmic components have been observed.

 

7. RESULTS AND DISCUSSIONS

In this paper, we proposed some weighted hybrid soft sets models. It is observed that, the investigator have a situation for selection to purchase as the quality nail polish after giving weights to numerous standards. A weight function to apply, W: A→ [0,1] and fuzzy-soft-set σ= (F ̃, A) is transformed into a weighted fuzzy-soft-set (F ̃, A, W). The optimal choice value is obtained on the preference weights. Feng-rough-soft-sets are used to explore specific decision-making procedures and get several most beneficial solutions. We explore the use of weighted fuzzy-soft-sets and provide a novel technique for solving the selection-making problem based on the rough soft-sets proposed by Ma et al. (2017). It is advisable to use level soft sets on decision-making issues with insufficient data in practical problems of real-world. We develop two distinctive types of selection-making techniques for rough, soft sets. Under these circumstances, the nearest and optimal cosmic components have been observed. Feng et al. (2011) confined the usage of Feng-soft-rough-sets. Shabir et al. (2013) extended the work of Feng et al. (2011) for multi-criteria decision-making and introduced a new multi-soft, rough set (MSR-set). We discuss an organizational decision-making problem based on an MSR-set with a hybrid model for optimal solutions.

 

8. CONCLUSIONS

In this paper, we expand on the notion of the characteristic function for soft sets and fuzzy soft sets by addressing the membership function for fuzzy soft sets. A novel approach for communal decision-making is presented by combining rough sets with soft sets. Two distinctive types of selection-making techniques for rough, soft sets are developed. Under these circumstances, the nearest and optimal cosmic components have been obtained. It also presents the use of soft, rough sets for item appraisal and group decision-making. A unique method provides that based on MSR-sets to handle the problem of multi-criteria decision-making and address real-world situations. The algorithms created for decision-making may be placed in more intricate hybrid soft set models for a hassle-free environment.

 

9. Conflict of interest

The authors declared that, in this manuscript no conflict of interests has been taken. 

 

10. Data Availability Statements

All data generated or analysed during this study are included in this published article Ma et al. (2017).

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Agarwal, R., Nishad, A. K., Agrawal, A., & Husain, S. (2023). Evaluation and Selection of a Green and Sustainable Supplier by Using a Fuzzy Aras Mathematical Modeling. New Mathematics and Natural Computation.   https://doi.org/10.1142/S1793005723500382.

Akram, M., Shahzadi, S., Rasool, A., & Sarwar, M. (2022). Decision-Making Methods Based on Fuzzy Soft Competition Hypergraphs. Complex & Intelligent Systems, 8(3), 2325-2348. https://doi.org/10.1007/s40747-022-00646-4.

Begam, S. S., Selvachandran, G., Ngan, T. T., & Sharma, R. (2020). Similarity Measure of Lattice Ordered Multi-Fuzzy-Soft-Sets Based on Set Theoretic Approach and its Application in Decision Making. Mathematics, 8(8), 1255. https://doi.org/10.3390/math8081255.

Chen, Z. H., Wan, S. P., & Dong, J. Y. (2022). An Efficiency-Based Interval Type-2 Fuzzy Multi-Criteria Group Decision Making for Makeshift Hospital Selection. Applied Soft Computing, 115, 108243. https://doi.org/10.1016/j.asoc.2021.108243.

Dalkılıç, O. (2021). A Novel Approach to Soft Set Theory in Decision-Making Under Uncertainty. International Journal of Computer Mathematics, 98(10), 1935-1945. https://doi.org/10.1080/00207160.2020.1868445.

Feng, F., Jun, Y. B., Liu, X., & Li, L. (2010). An Adjustable Approach to Fuzzy-Soft-Set Based Decision Making. Journal of Computational and Applied Mathematics, 234(1), 10-20. https://doi.org/10.1016/j.cam.2009.11.055.

Husain, S., & Shivani, K. (2018). A Study of Properties of Soft Set and its Applications. International Research Journal of Engineering and Technology (IRJET), 5(01), 2395-0056.

Husain, S., Kumari, A., & Tyagi, V. K. (2022). An Approach to Group Decision Problems Using Fuzzy-Soft-Set Theory and Lambda Cuts. International Journal of Early Childhood Special Education (INT-JECSE), 14(8).  

Husain, S., Tyagi, V. K., & Gupta, M. K. (2022). A Fuzzy Soft Set-Theoretic New Methodology to Solve Decision-Making Problems. In Electronic Systems and Intelligent Computing: Proceedings of ESIC 2021 Singapore: Springer Nature Singapore. 671-683. https://doi.org/10.1007/978-981-16-9488-2_64.

Jana, C., & Pal, M. (2018). Application of Bipolar Intuitionistic Fuzzy-Soft-Sets in Decision Making Problem. International Journal of Fuzzy System Applications (IJFSA), 7(3), 32-55. https://doi.org/10.4018/IJFSA.2018070103.

Khalil, A. M., & Hassan, N. (2019). Inverse Fuzzy-Soft-Set and its Application in Decision Making. International Journal of Information and Decision Sciences, 11(1), 73-92. https://doi.org/10.1504/IJIDS.2019.096630.

Kong, Z., Gao, L. & Wang, L. (2009). Comment on a Fuzzy-Soft-Set Theoretic Approach to Decision Making Problems. Journal of Computational and Applied Mathematics, 223(2), 540-542. https://doi.org/10.1016/j.cam.2008.01.011.

Ma, X., Liu, Q., & Zhan, J. (2017). A Survey of Decision Making Methods Based on Certain Hybrid Soft Set Models. Artificial Intelligence Review, 47(4), 507-530. https://doi.org/10.1007/s10462-016-9490-x.

Maji, P. K., Roy, A. R., & Biswas, R. (2002). An Application of Soft Sets in a Decision Making Problem. Computers & Mathematics with Applications, 44(8-9), 1077-1083. https://doi.org/10.1016/S0898-1221(02)00216-X.

Molodtsov, D. (1999). Soft Set Theory-First Results. Computers & Mathematics with Applications, 37(4-5), 19-31. https://doi.org/10.1016/S0898-1221(99)00056-5.

Rahman, A. U., Saeed, M., Khalifa, H. A. E. W., & Afifi, W. A. (2022). Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Math, 7(3), 3866-3895. https://doi.org/10.3934/math.2022214.

Riaz, M., & Tehrim, S. T. (2019). Bipolar fuzzy soft mappings with application to bipolar disorders. International Journal of Biomathematics, 12(07), 1950080. https://doi.org/10.1142/S1793524519500803.

Roy, A. R., & Maji, P. K. (2007). A Fuzzy-Soft-Set Theoretic Approach to Decision Making Problems. Journal of Computational and Applied Mathematics, 203(2), 412-418. https://doi.org/10.1016/j.cam.2006.04.008.

Shabir, M., Ali, M. I., & Shaheen, T. (2013). Another Approach to Soft Rough Sets. Knowledge-Based Systems, 40, 72-80. https://doi.org/10.1016/j.knosys.2012.11.012.

Yang, Y., Tan, X., & Meng, C. (2013). The Multi-Fuzzy-Soft-Set and its Application in Decision Making. Applied Mathematical Modelling, 37(7), 4915-4923. https://doi.org/10.1016/j.apm.2012.10.015.

Zadeh, L. (1965). Fuzzy sets. Inform Control, 8, 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X.

Zulqarnain, R. M., Xin, X. L., Saqlain, M., & Khan, W. A. (2021). Topsis Method Based on the Correlation Coefficient of Interval-Valued Intuitionistic Fuzzy-Soft-Sets and Aggregation Operators with their Application in Decision-Making. Journal of Mathematics, 1-16. https://doi.org/10.1155/2021/6654657.

Çağman, N., & Karataş, S. (2013). Intuitionistic Fuzzy-Soft-Set Theory and its Decision Making. Journal of Intelligent & Fuzzy Systems, 24(4), 829-836. https://doi.org/10.3233/IFS-2012-0601.