EXCHANGE RATE RISK IN A NEWSVENDOR FRAMEWORK UNDER A GAMMA- DISTRIBUTED EXCHANGE RATE ERROR AND ISOELASTIC DEMAND

 

Zarana Mehta ¹, Ravi Gor ²

 

¹ Research scholar, Department of Mathematics, Gujarat University, Ahmedabad, India

² Department of Mathematics, Gujarat University, Ahmedabad, India

 

1. INTRODUCTION

Forex exposure refers back to the risk related to the foreign exchange rates that alternate frequently and may have a detrimental effect on the financial transactions denominated in some foreign currency rather than the local currency of the agency. In short, the company’s risk that its future cash flow gets affected by the exchange within the cost of the foreign currency.

A hazard confronted via the company that whilst dealing within the global change, the currency rate can also change earlier than making the final settlement, is called as a Transaction exposure. The greater the time gap among the agreement and the final agreement, the higher is the risk associated with the trade inside the forex prices. Arcelus et al. (2013) have invented a mathematical model in news vendor framework to find maximum favourable ordering and pricing techniques for exporter and manufacturer, when the two international locations doing the business, faces transaction exposure. The entire derivation of optimum techniques and predicted profit of the exchange rate risk model for multiplicative demand is given in Patel and Gor (2015). Our main contribution on this paper is to give an explanation for the effect of gamma distribution within the exchange rate error under the isoelastic demand with multiplicative error in news vendor setting.

 

2. LITERATURE REVIEW

This paper follows Arcelus et al. (2013) mathematical model. Transaction exposures by firms with receivables or payables in foreign currencies have been modeled in Goel (2012). It is the nature of global trade that a buyer or a seller must bear what is known in the international finance field as transaction exposure, Eitemann et al. (2010), Shubita et al. (2011).

By Petruzzi and Dada (1999), a newsvendor framework was invented. The price dependent demand forms in the additive and multiplicative error by Mills (1958), Karlin and Carr (1962) have been used. In Patel and Gor (2015), the maximum profit and ideal techniques are derived for linear demand forms and for multiplicative demand forms. A new hybrid model was developed for additive and multiplicative demand errors (2015). In a Newsvendor framework, Mehta and Gor (2020) modeled exchange rate errors under Gamma distribution. The

effect of a log-normal distribution on the exchange rate error under linear demand in news vendor settings is modeled by Mehta and Gor (2020). The authors have also developed a model for the exchange rate error under a Gumbel distribution (2021) and under Exponential distribution (2022).

 

3. TRANSACTION EXPOSURE MODEL

If exporter intend to buy q units from a foreign producer of some product. The exporter is not very well aware about the demand(D) of the product, which is uncertain. But the demand depends on the price(p), and it is uncertain. In this paper, we consider the price dependent demand with multiplicative error which can be given as,

, where 𝜖 is the multiplicative error in the demand and it follows some distribution with mean 𝜇 in interval [A, B] and  is the multiplicative demand error.

Let us denote exchange rate as ‘𝑟’ in the exporter currency when the order is confirmed. Let 𝑤 denotes the cost of one unit of the product in the producer currency. If buyer gives the payment on the day of settlement, then he has to pay 𝑤𝑟 per unit of the product in his currency. Suppose there is a time lag between placing of order and the release of payment for the product, there exists transaction exposure risk, since the exchange rate may differ. So, the buyer must pay more or less, depends on the prevailing rate on the day delivery of the product. We model future exchange rate as,

FER= Current exchange rate+ fluctuation in the exchange rate.

The difference in the exchange rate is some percentage of 𝑟, so we take FER= , where 𝜖_𝑟 is a random variable together with the variable 𝐷. We consider 𝜖_𝑟 lies in [−𝑎, 𝑎]. Here, . The value of 𝜖_𝑟 is unknown but it depends on distribution . In this paper we assume gamma distribution for 𝜖_𝑟 with support [𝑎, 𝑏] i.e., . The expected value of the fluctuation in exchange rate is, . If the exchange rate fluctuation  is positive, buyer must pay more and if it is negative then seller will get less. So, who will bear the exchange rate risk? In this paper, we will discuss two scenarios under multiplicative demand error. In both the cases, the exporter’s optimal policy is to determine the optimum order (q) and selling price (p) of the product. So, his expected profit is maximum. Also, we will obtain the strategies for producer as well.

 

4. ASSUMPTIONS AND NOTATIONS

We will use the following presumptions in the foreign exchange transaction exposure model:

1)     The standard newsvendor problem assumptions apply.

2)     The global supply chain consists of single exporter-single producer.

3)     The error in demand is multiplicative.

4)     Only one of the two-exporter or producer- bears the exchange rate risk.

The following notations are used in the paper:

·       q= order quantity

·       p= selling price per unit

·       D= demand of the product= no. of units required

·       𝜖= demand error= randomness in the demand.

·       V= salvage value per unit

·       s=penalty cost per unit for shortage

·       c= cost of manufacturing per unit for manufacturer

·       wr = purchase cost for retailer

·       𝜖_𝑟= the exchange rate fluctuation= exchange rate error= randomness in exchange rate

·       Π= profit function.

 

The two Scenarios

Case 1: Exporter bears the exchange rate risk

Assume that exporter bears the exchange rate risk and producer does not bear. Hence, the producer will get 𝑤 per unit at any time and the buyer must pay according to the existing exchange rate. So, buyer will pay  per unit, on the settlement day. This amount in producer’s currency is  . Hence, 𝑊𝑟 is the purchase cost to buyer in seller’s currency. Now, the exporter will choose the selling price p & order quantity q, to maximize his expected profit. The profit function of the exporter is given by,

 

Π (𝑝, 𝑞) = [revenue from q items]– [expenses for the q items]

                   

 

All the parameters 𝑝, 𝑣, 𝑠, 𝑤𝑟 are taken in producer’s currency and the salvage value 𝑣 is taken as an income from the disposal of each of the  leftovers.

Since, the demand  the exporter’s profit function is given by,

 

                                           

 

Putting  and define  for the multiplicative demand error. Now, and similarly  

 

                                                              (2)

 

The equation (2) describes the profit function for the retailer in the manufacturer currency. Note that the parameter q is replaced by z. Now the retailer wants to find the optimal order quantity q say q* and optimal price p= p* to maximize his expected profit. In order to do this, he must find optimal values of the price p and the parameter z, say p* and z* respectively which maximizes his expected profit so that he can determine the optimal order q*=z*g(p*). The profit Π is a function of the random variable ∈ with support [A, B]. Thus, the retailer’s expected profit is given by,

 

 

Define [expected leftovers] and

 

 [expected shortages]

 

Then the expected profit of the retailer as a function of z and p is given by,

 (4) as derived in Sanjay Patel and Ravi Gor. Where  in the equation (4) and it gives the expected value of the randomness u in the demand D.

We use whitin’s method to maximize the expected profit function. In this method first we keep p fixed in (4) and use the second order optimality conditions  to find the optimum value of 𝑧∗ as a function of function p. Then we substitute the value of 𝑧∗ in the expected profit (4) so that it becomes a function of single variable p and hence the optimal p* can also be obtained. The authors have already derived the optimal policies given below, in Patel and Gor (2015)

 

 (5) where  is the CDF.

 

The retailer’s optimal order quantity 𝑞 = 𝑞∗ is given by

 

                                                                        (6)

 

Also, the manufacturer’s profit when the buyer bears the risk is [(selling price of seller) - (cost of purchase to seller)] × no. of units sold,

 

                                                                                                                    (7)

 

Case: 2 Seller bears the exchange rate risk

We assume that the manufacturer bears the exchange rate risk and retailer does not. Thus, the retailer pays w per unit in manufacturer’s currency at any point of time and the manufacturer will get according to the existing exchange rate. So, the manufacturer will be getting   per unit on the settlement day in his currency. Now the retailer’s profit function, his expected profit, and optimal policies to get maximum expected profit can be obtained by replacing wr by w in case 1. So, we get the retailer’s profit as,

 

                            (8)

 

And his expected profit as,

 

                                     (9)

 

The optimal value of z is given by  and hence the optimum order quantity is,  (10). Also, the manufacturer’s profit when the buyer bears the risk is [(selling price of seller) - (cost of purchase to seller)] × no. of units sold,

 

                                                                                                            (11)

 

5. SENSITIVITY ANALYSIS

Here, we have considered isoelastic demand with multiplicative demand error 𝑢 which follows the uniform distribution  with support [A, B]. We get the ideal strategy and maximum expected profit of the exporter and producer using MAPLE software when either exporter or producer takes the exchange rate risk. We figure out the ideal optimum values by using gamma distribution  in the exchange rate error  with support [0.1,0.2]. The probability density function of gamma distribution is,

 

with mean 𝐸[𝑋] = 𝑘𝜃 and standard deviation

 

We will consider following parameter values:

Demand support= [A, B] = [0.7,1.1]

Mean demand= 2

Isoelastic demand

Salvage value

Penalty cost 𝑠 = 5

Cost of producing per unit for producer 𝑐 = 20

Current exchange rate 𝑟 = 45

The following tables in case-I and case-II we get using MAPLE software.

 

5.1. MAPLE code for Gamma distribution when exporter bears the risk

The expected value of the exchange rate error er=erx in [el,eu] using generalized gamma probability density function is:

 

 

                                                        

 

 

 

 

 

           

 

 

            

 

                                                   

 

       

 

                                

 

 

 

                      

 

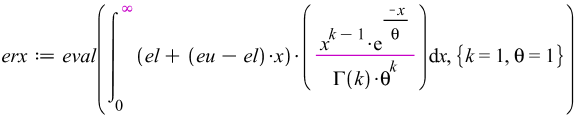
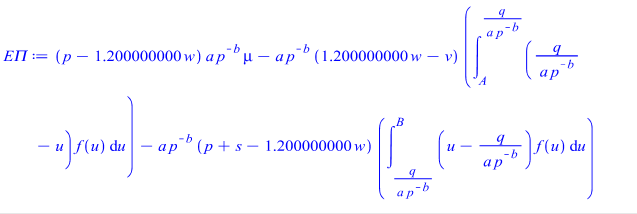
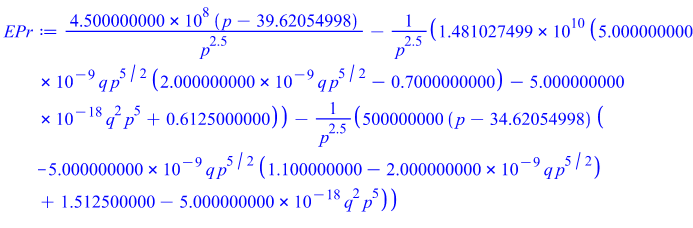
5.2. MAPLE code for gamma distribution when producer bears the risk

With gamma distribution seller bears the risk with isoelastic demand and multiplicative error

 

                                        

 

                                         

                                                                              

                                                              

                                                                                       

                                                                                    

                                                                                      

                                                                                                          

                                                                                    

 

                           

                        

 

                         

         

 

                 

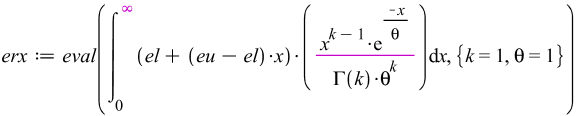
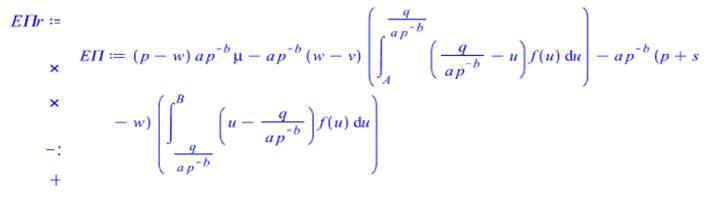
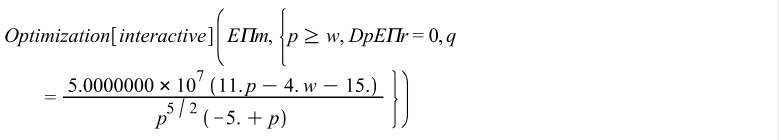
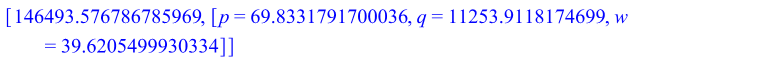
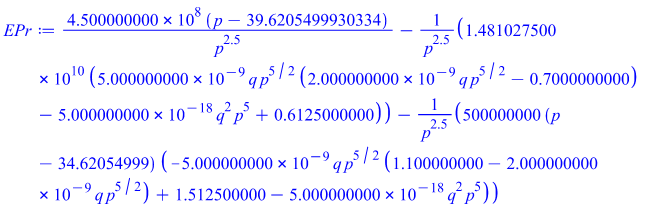
Table 1

Table 1 Gives the Observations by Taking Different Values of Parameters of The Gamma Distribution When Exporter Bears the Risk.
Distribution	Parameters of the Distribution	p*	q*	Seller’s selling price w*	Optimum expected profit of buyer	Optimum expected profit of seller
Gamma	𝑘 = 1, 𝜃= 3	81.58	7569.81	33.09	232042.73	99164.24
	𝑘 = 3, 𝜃= 1	81.58	7569.81	33.09	232042.73	99164.24
	𝑘 = 1, 𝜃= 1	69.83	11253.91	33.01	294139.11	146493.57
	𝑘 = 1, 𝜃= 2	75.71	9155.63	33.06	260002.64	119603.50
	𝑘 = 2, 𝜃= 3	99.13	4612.99	33.17	172507.91	60769.09
	𝑘 = 3, 𝜃= 2	99.13	4612.99	33.17	172507.91	60769.09

 

Table 2

Table 2 Gives the Observations by Taking Different Values of Parameters of the Gamma Distribution When Producer Bears the Risk.
Distribution	Parameters of the distribution	P*	q*	Seller’s selling price w*	Optimum expected profit of buyer	Optimum expected profit of seller
Gamma	𝑘 = 1, 𝜃= 3	74.68	9471.42	42.39	265499.26	97472.85
	𝑘 = 3, 𝜃= 1	74.68	9471.42	42.39	265499.26	97472.85
	𝑘 = 1, 𝜃= 1	69.83	11253.91	39.62	294139.11	146493.57
	𝑘 = 1, 𝜃= 2	62.41	15000	35.38	349216.91	108278.41
	𝑘 = 2, 𝜃= 3	62.41	15000	35.38	349216.91	12212.90
	𝑘 = 3, 𝜃= 2	62.41	15000	35.38	349216.91	12212.90

 

6. CONCLUSION

We expand exchange rate fluctuation using gamma distribution when the retailer or manufacturer accepts to share the exchange rate risk with multiplicative demand error in news vendor framework.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Arcelus, F.J., Gor, R. M., and Srinivasan, G. (2013).Foreign Exchange Transaction Exposure in a Newsvendor Setting, European Journal of Operational Research, 227(3), 552-557. https://doi.org/10.1016/j.ejor.2012.10.014.

Eitemann, D.K., Stonehill, A.I., and Moffett, M.H. (2010). Multinational Business Finance, 12th Ed.Prentice Hall, Boston.

Goel, M. (2012). Management of Transaction Exposure: A Comparative Analysis of Mncs in India. International Journal of Service Science, Management, Engineering and Technology3, 37-54. https://doi.org/10.4018/jssmet.2012010103.

Karlin, S., and Carr, C.R. (1962).  Prices and optimal inventory policy. In : Arrow, K.J., Scarf, H. (Eds.), Studies in Applied Probability and Management Science. Stanford University Press, Palo Alto, CA, 159-172.

Mehta, Z., Gor, R. (2020)."Mathematical Model of Foreign Exchange Risk in a Supply Chain with Newsvendor Setting using a Log- Normally Distributed Exchange Rate Error." IOSR Journal of Economics and Finance (IOSR-JEF), 11(5), 48-57.

Mehta, Z., Gor, R. (2020). Transaction Exposure Model under Gamma Distribution Exchange Rate Error in a Newsvendor Framework, Alochana Chakra Journal, 9(6), 4028-4032.

Mehta, Z., Gor, R. (2021)."Transaction Exposure Model Using Gumbel Distribution Exchange Rate Error in a Newsvendor Framework." IOSR Journal of Mathematics (IOSR-JM), 17(3), 39-47.  

Mehta, Z., Gor, R. (2022)."Transaction Exposure Model Under Exponential Distribution Exchange Rate Error with Newsvendor Setting", 14(3), 25-36.

Mills, E.S. (1958). Uncertainty and price theory, Quarterly Journal of Economics 73, 116-130. https://doi.org/10.2307/1883828.

Patel, S. and Gor, R. (2016a). A Newsvendor Framework of Exchange Rate Risk with Uniformly Distributed Exchange Rate Error, International Journal of Research in Engineering and Technology, 5(5), 412-416. https://doi.org/10.15623/ijret.2016.0505079.

Patel, S. and Gor, R. (2016b). A Newsvendor Framework of Transaction Exposure Model With Uniformly Distributed Exchange Rate Error and Isoelastic Demand, International Journal of Science, Engineering and Technology Research, 5(6), 1904-1908.

Patel, S., and Gor, R. (2015). Exchange Rate Risk Sharing Contract Model, IOSR Journal of Mathematics (IOSRJM), 11(2), 47-52.

Patel, S., and Gor, R. (2015). Transaction Exposure Risk Modelled in a Newsvendor Framework Under the Multiplicative Demand Error, IOSR Journal of Mathematics (IOSR -JM),11(2), 53-59.

Patel, S., and Gor, R. (2015). Exchange Rate Risk Sharing Contract Model, IOSR Journal of Mathematics (IOSRJM), 11(2), 47-52.

Patel, S., and Gor, R. (2015). Foreign Exchange Transaction Exposure Within a Newsvendor Frame Work Under Hybrid Demand Distribution- IOSR Journal of Mathematics (IOSR-JM), 11(5), 51-58.

Petruzzi, N.C., and Dada, M. (1999). Pricing and the Newsboy Problem: A Review with Extensions. Operations Research 47, 183-194. https://doi.org/10.1287/opre.47.2.183.

Patel, S. and Gor, R. (2016). Exchange Rate Risk in a Newsvendor Framework with Normally Distributed Exchange Rate Error, International Journal of Mathematics Trends and Technology, 34(2), 54-58. https://doi.org/10.14445/22315373/IJMTT-V34P512.

Shubita, M.F., Harris, P., Malindretos, J., and Bobb, L.M. (2011). Foreign Exchange Exposure: An Overview. International Research Journal of Finance and Economics 78, 171- 177.

Whitin, T.M. (1955). Inventory Control and Price Theory, Management Science, 2(1), 61-68. https://doi.org/10.1287/mnsc.2.1.61.