Digital Image Encryption using Laplace Transform and LFSR

 

Srushti Gandhi ¹ , Ravi Gor ²,

 

¹ Research Scholar, Department of Mathematics, Gujarat University, Gujarat, India

² Department of Mathematics, Gujarat University, Gujarat, India

 

1. INTRODUCTION

In the present world, technologies have been progressing rapidly. Primarily, most people prefer to use internet to transfer data from sender to receiver. There are several ways to transmit data such as e-mail, message, whatsapp, and many more. In the present communicating world, images are used widely. Yet security and authenticity are the main issue for sending data through internet. Data security means protection of data from attackers and unauthorised parties/users. Encryption is one of the best techniques to secure data. Image encryption is a technique that converts original image into cipher image which is difficult to identify. No one can access image without knowing the decryption key. Image encryption process has applications in various fields like in corporate world, health care, military, multimedia etc.

Cryptography plays key role in the field of security. It is the battlefield for mathematicians and scientists. Cryptography consists of encryption and decryption process. Encryption is the process of converting plain text into cipher text. Decryption is the reverse process of encryption i.e., the process of converting cipher text into plain text. Several cryptographic algorithms have been proposed till date such as AES, DES, RSA, IDEA, etc.

Image encryption techniques are different from data encryption techniques. There are several security problems for digital image processing and transmission. So, it is necessary to maintain integrity and confidentiality of an image. Any single change in the pixel value does not change the entire image. Thus, digital images are less sensitive than data. A small manipulation or modification in digital image is acceptable as compared to text message. But it is more susceptible to decrypt by an attacker.

Various images are transmitted and stored in large amount over wireless network and internet. Thus, there is rapid development in multimedia and network technology. Digital image plays significant role in multimedia technology. Thus, it is important for the user to maintain privacy as well as security. To provide privacy and security to the users, digital image encryption and decryption process is important to protect from any unauthorised parties/user. Image, audio, and video encryption have applications in various fields like internet communications, multimedia, medical imaging, military etc.

 

2. LITERATURE REVIEW

Anandkumar (2015) proposed an image encryption algorithm that worked efficiently. It is very secure, with a prominent level of security and low computational requirements. The simulation results that the method had advantages based on their image-processing approaches. As a result, the algorithms are found to be effective for image encryption. It can provide security in open networks.

Kapur et al. (2015) planned a simple and secure procedure to secure images. The image encryption procedure made use of two Pseudo Random Number generators. In the first step, Linear Feedback Shift Register algorithm was used to swap the rows of the original image. This was followed by the swapping of the columns. This produced an intermediary cipher image. In the second step, Blum Blum Shub algorithm was used to substitute the intensity of each pixel of the intermediary cipher image. This produced the final encrypted image.

Mondal et al. (2016) proposed a highly secure encryption algorithm. They used permutation-substitution architecture for encryption and decryption of an image. In the permutation step, image pixels of the plain image are shuffled using Linear Feedback Shift Register (LFSR). The output of this step is an intermediary cipher image which is of the same size as that of the plain image. In the substitution step, sequence of random numbers was generated using the RC4 key stream generator. It was XORed with the pixel value of the intermediary cipher image to produce the final cipher image. Experimental results and security analysis of the proposed scheme show that the proposed scheme is efficient and secure.

Chepuri (2017) projected Laplace Transform algorithm for encrypting images. The Laplace Transform algorithm has been updated to work with RGB images. The results of the experiments showed that they were able to successfully encrypt and decrypt a variety of images, and that the technique has a decent encryption effect. When compared to the original image, the cipher image created by their technology was completely different. This method offers enhanced security and is appropriate for secure image transmission over the Internet.

Jumaa (2018) solved the problem of secret key exchanging with the communicated parities by using a random number generator based on Linear Feedback Shift Register (LFSR). The random key generator was used to encrypt and decrypt the data using the Advance Encryption Standard (AES). They also encrypted and decrypted grayscale and colour RGB images. Three elements were important to the functionality of their proposed system in their paper: The first feature dealt with the obstetrics of creating a random and safe encryption key, the second with encrypting the plain or secret image using the AES technique, and the third with recovering the original image by decrypting the encrypted or cipher one.

Devi et al. (2018) proposed a new medical image encryption algorithm. For image confusion, they applied a Henon map, and for diffusion, they used a Linear Feedback Shift Register (LFSR). The researchers looked at metric values and claimed that their system could withstand differential attacks. They show that their approach can ensure the security of DICOM images.

Jain and Sharma (2019) presented a technique for digital image encryption which is enhancing its security by using the Laplace Transform Algorithm.

 

3. TERMINOLOGIES

3.1.  LAPLACE TRANSFORMATION Anandkumar (2015)

Laplace Transformation is a technique for solving differential equations. Here, differential equation of time domain formed is first transformed to algebraic equation of frequency domain. After solving the algebraic equation in frequency domain, the result is then finally transformed to time domain to achieve the ultimate solution of the differential equation. In other words, it can be said that the Laplace Transformation is nothing but a shortcut method of solving differential equation.

The Laplace Transforms is usually used to simplify a differential equation into a simple and solvable algebra problem. Even when the algebra becomes a little complex, it is still easier to solve than solving a differential equation.

Let  be the function of  time, for all ; then the Laplace Transform of  can be defined as:

Provides that the integral exists. Where the Laplace Operator,   will be real or complex .

 

Some of the Laplace Transformation properties are:

1)     Linearity: Let ,  be constants. , be the functions of time, , then

 

2)     Change of scale property:

If , then

; frequency scaling

; time scaling

 

3)     Differentiation:

And many more.

 

3.2. LINEAR FEEDBACK SHIFT REGISTER (LFSR) Devi et al. (2018),  Srushti and Gor (2022)

LFSR is a shift register whose input is liner function of its previous state. LFSR is built from simple shift register with a small number of XOR gates. Shift register is a type of digital circuit using a cascade of flipflops where the output of one flipflop is connected to the input of the next.

Initial value of LFSR is called seed. LFSR consists of clocked storage elements (flipflops) and a feedback path. The number of storage elements gives degree of LFSR. LFSR with  flipflops is said to be of  degree. As operation of register is deterministic, the stream of values produced by register is determined by its current state. As register has finite number, if possible, states it must eventually enter a repeating cycle. LFSR with well-chosen feedback function can produce a sequence of bits that appears random and has exceptionally long cycle. LFSRs are  bits counter exhibiting pseudorandom behaviour.

An m-stage linear feedback shift register (LFSR) is characterized by feedback polynomial of degree-m over , if the feedback polynomial is primitive the sequence of states generated is periodic and is of period .Here, . There are 255 possible initial states. Each initial state generates a periodical sequence of states of periodic the sequence of states of the period.The sequence generated with different initial states are shifted versions of each other.

Figure 1

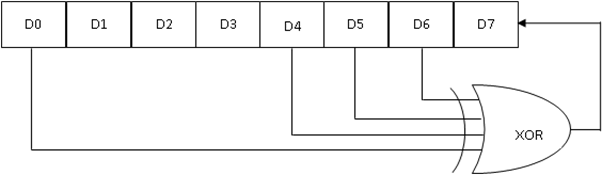
Figure 1 LFSR

 

LFSRs are used in many key stream generators because:

·        LFSRs are well suited to hardware implementation.

·        They can produce sequences with good statistical properties.

·        They can produce sequences of large period.

·        Because of their structure, they can be rapidly analysed using algebraic techniques.

In the purposed scheme, sequences of 8 bit are used for generating key sequences. We denote this sequence as .

 

4. PROPOSED WORK

4.1. ENCRYPTION ALGORITHM

Step 1: An 8-bit image of size  pixels converted into a one-dimensional array of pixel  , where  and  Next, convert each unsigned pixel value ranging from 0 to 255 into a block of 8-bit.

 

Step 2: Bit by bit XOR operation is employed between generated sequence  which is generated by Laplace Transform and which is generated by LFSR using by  to obtain final key sequence .

 

 

Step 3: The binary image pixels  are XORed with key sequence {Ki} to obtain encrypted pixel . This block of 8-bit is intern converted into decimal digit   0 to 255.

 

Step 4: Repeat step 3 to encrypt all image pixels. Transform all encrypted digits   into an array of size to obtain the encrypted image.

 

4.2. DECRYPTION ALGORITHM

Step 1: Encrypted image of size  pixels is transformed into one dimensional array of pixels  , where  and  . Then convert each unsigned pixel values into a block of 8 bit.

 

Step 2: The key sequence  is obtained by  and  as defined in (3) is used to decrypt the image. The obtained block of decrypted 8-bit  is converted into decimal digits and called as .

 

 

Step 3: One dimensional array of decrypted pixels  is converted into an array of size  to obtain the decrypted image.

 

 

 

 

 

 

 

 

 

 

 

5. EXAMPLE

Figure 2

Figure 2 Original Image

 

Using PYTHON.

Image array: <PIL.JpegImagePlugin. JpegImageFile image mode=RGB size=576x720 at 0x182A11243D0>

Numpy array: <class 'numpy. ndarray'>

Image shape: (720, 576, 3)

Pillow image: <class 'PIL.Image.Image'>

Image mode: RGB

Image size: (576, 720)

Image array/in matrix form:

Total pixel value: 284832

 

1)     Key generation using Laplace Transformation:

Using , the output is . On considering the coefficient of the given output, binary of  is .

 

This binary is used to generate key for LFSR.

 

2)     Key generation using LFSR:

Using Laplace Transform key  and a primitive polynomial ; we have.

1.0011E+11	0
1.0011E+10	1
1.001E+12	0
1.001E+11	1
1.01E+12	0
1.01E+11	1
……….
1.1101E+10	1
1.0011E+12	(Repeating)

 

Here, from  clock, period will be repeating and will give pseudorandom sequence. So, 0011101100001 is considered as key .

 

5.1.  FOR XOR OPERATION

5.1.1.   ENCRYPTION ALGORITHM

Step 1: An 8-bit grayscale image of size  pixels converted into a one-dimensional array of pixel . where  and  Next, convert each unsigned pixel value ranging from 0 to 255 into a block of 8-bit.

A one-dimensional array of pixel :

 

 

 

 

Step 2: Bit by bit XOR operation is employed between generated sequence  which is generated by Laplace Transform and which is generated by LFSR using by  to obtain final key sequence .

 

 

Input a binary number: .

The decimal value of the number is .

 

Step 3: The binary image pixels  are XORed with key sequence {Ki} to obtain encrypted pixel .  This block of 16-bit is intern converted into decimal digit   0 to 255.

 

 

Step 4: Repeat step 3 to encrypt all image pixels. Transform all encrypted digits       into an array of size to obtain the encrypted image.

Figure 3

                               Unit 16

Figure 3 Encrypted XOR Image

 

For encrypted image:

Image array: <PIL.PngImagePlugin. PngImageFile image mode=I size=1728x720 at 0x1829FEEFE50>

Numpy array: <class 'numpy.ndarray'>

Image shape: (720, 1728)

Pillow image: <class 'PIL.Image.Image'>

Image mode: I

Image size: (1728, 720)

Image array/in matrix form:

                                      

                                        

                                        

                                                                  

                                        

                                        

                                        

Total pixel value: 3732480

 

5.1.2.  DECRYPTION ALGORITHM

Step 1: Encrypted grayscale image of size  pixels is transformed into one dimensional array of pixels  ,where  and  . Then convert each unsignd pixel values into a block of 16 bit.

 

 

Step 2: The key sequence  is obtained by  and  as defined in (3) is used to decrypt the image. The obtained block of decrypted 8-bit  is converted into decimal digits and called as .

 

 

 

Step 3: One dimensional array of decrypted pixels  is converted into an array of size  to obtain the decrypted image.

 

Figure 4

 

 

 

 

 

 

 

 

Figure 4 Decrypted XOR image

 

5.2.  XNOR OPERATION

5.2.1.  ENCRYPTION ALGORITHM

Step 1: An 8-bit grayscale image of size  pixels converted into a one-dimensional array of pixel . where  and  Next, convert each unsigned pixel value ranging from 0 to 255 into a block of 8-bit.

A one-dimensional array of pixel :

 

Step 2: Bit by bit XOR operation is employed between generated sequence  which is generated by Laplace Transform and which is generated by LFSR using by  to obtain final key sequence .

 

 

Input a binary number: .

The decimal value of the number is .

 

Step 3: The binary image pixels  are XORed with key sequence {Ki} to obtain encrypted pixel . This block of 16-bit is intern converted into decimal digit   0 to 255.

 

 

Step 4: Repeat step 3 to encrypt all image pixels. Transform all encrypted digits     into an array of size to obtain the encrypted image. Unit 8

 

 

Figure 5

Figure 5 Encrypted XNOR Image

 

For encrypted image:

Image array: <PIL.PngImagePlugin. PngImageFile image mode=I size=1728x720 at 0x1829FEEFE50>

Numpy array: <class 'numpy.ndarray'>

Image shape: (720, 1728)

Pillow image: <class 'PIL.Image.Image'>

Image mode: I

Image size: (1728, 720)

Image array/in matrix form:

Total pixel value: 3732480

 

5.2.2.  DECRYPTION ALGORITHM

Step 1: Encrypted grayscale image of size  pixels is transformed into one dimensional array of pixels  ,where  and  . Then convert each unsigned pixel values into a block of 16 bit.

 

 

Step 2: The key sequence  is obtained by  and  as defined in (3) is used to decrypt the image. The obtained block of decrypted 8-bit  is converted into decimal digits and called as .

 

 

 

Step 3: One dimensional array of decrypted pixels  is converted into an array of size  to obtain the decrypted image.

 

 

 

Figure 6

 

 

 

 

 

 

 

 

Figure 6 Decrypted XNOR image

 

6. RESULTS AND DISCUSSION

6.1. Visual Testing

The visual testing is done online on https://www.textcompare.org/image/.

Figure 7

Figure 7 Visual Testing

 

Comparing original and encrypted image, similarity between them is shown in the below table. White dotes show the similar pixel values of original image and encrypted image.

By comparing original image with encrypted image and decrypted image, the difference is shown in below table. The white dot indicates the similar pixel value of original image and encrypted image. The difference is found with full transparency when less ignored along with original size and movement with different intensity.

 

 

 

 

Figure 8

Figure 8 Difference between original and encrypted XOR image

 

Figure 9

Figure 9 Difference between original and decrypted XOR image

 

Image	Difference
Original and Encrypted XOR image	98.12 %
Original and Decrypted XOR image	0.18 %

 

 

 

 

Figure 10

Figure 10 Difference between original and encrypted XNOR image

 

 

Figure11

Figure 11 Difference between original and decrypted XNOR image

 

Image	Difference
Original and Encrypted XNOR image	98.59 %
Original and Decrypted XNOR image	0.18 %

 

Image	Difference
Original and Encrypted image	94.35 %
Original and Decrypted image	0.18 %

 

 

 

 

By comparing original image with encrypted image and decrypted image, the difference is shown in below table. The white dot indicates the similar pixel value of original image and encrypted image. The difference is found with full transparency when less ignored along with scale to same size and movement with different intensity.

Figure 12

Figure 12 Difference between original and encrypted image

 

 

 

 

 

 

 

Figure 13

Figure 13 Difference between original and decrypted image

 

Figure 14

Figure 14 Difference between original and encrypted XNOR image

 

Figure 15

Figure 15 Difference between original and decrypted XNOR image

 

Image	Difference
Original and Encrypted XNOR image	91.36 %
Original and Decrypted XNOR image	0.18 %

 

 

 

 

 

 

 

 

6.2.  SENSITIVITY ANALYSIS Srushti and Gor (2022)

Image quality and vision outcomes were generated because of the experiment. All the analysis are performed with the use of PYTHON. The following parameters are used to evaluate image quality:

 

6.2.1.  NUMBER OF PIXELS CHANGE RATE (NPCR)

When the difference between two encrypted images is negligible, NPCRs are used to verify the number of changing pixels between them. The NPCR can be mathematically defined as follows:

 

NPCR=

 

Where 

 

 is the weight and height of the encrypted interferogram,

 is the interferogram encrypted before pixel change,

 is the interferogram encrypted after pixel change,

 is the bipolar network

The optimal NPCR value is:

Image	NPCR
Encrypted XOR image	100%
Decrypted XOR image	0%
Encrypted XNOR image	100%
Decrypted XNOR image	0       %

 

6.2.2.  MEAN SQUARED ERROR (MSE) AND PEAK SIGNAL TO NOISE RATIO (PSNR)

The PSNR block analyses the peak signal-to-noise ratio between two images in decibels. The PSNR ratio is used to compare the quality of the original and encrypted images. The better the quality of the compressed or reconstructed image, the higher the PSNR.

To compare image compression quality, the mean square error (MSE) and peak signal-to-noise ratio (PSNR) are evaluated. The MSE is a measure of the peak error between the encrypted and original image, whereas the PSNR is a measure of the cumulative squared error.

The smaller the MSE value, the smaller the error.

The PSNR is calculated by first calculating the mean-squared error (MSE) using the equation:

 

MSE  

                                             

 

PSNR can be calculated as:

PSNR

            

 

The optimal MSE and PSNE values are:

Image	MSE	PSNR
Encrypted XOR image	4096	4096 dB
Decrypted XOR image	4096	4096 dB
Encrypted XNOR image	0	0 0 dB
Decrypted XNOR image	0	00    0 dB

 

6.2.3.  UNIFIED AVERAGE CHANGING INTENSITY (UACI)

UACI is used to calculate the average intensity of the difference between the two encrypted images ( and ). It is used to determine the strength of an encryption scheme. Its quality is determined by the format and size of the image. The average intensity variation between the ciphered and original images is measured using UACI. The highest UACI suggests that the recommended technique is resistant enough to a variety of attacks.

 

For an image of size , UACI is calculated as follows:

UACI  

 

On comparing the original image with encrypted image and decrypted image, the optimum UACI value is:

Image	UACI
Encrypted XOR image	40.96%
Decrypted XOR image	40.96%
Encrypted XNOR image	0%
Decrypted XNOR image	0       %

 

6.2.4.  ENTROPY ANALYSIS    

Information entropy is the degree of the uncertainty associated with a random event. It tells us the amount of information present in the event. It increases with uncertainty or randomness. It finds its application in various fields such as statistical inference, lossless data compression and cryptography. The entropy  of m can be calculated as:

 

where is the total number of symbols.

           and  is the probability of symbol .

In case of the original digital image,   should theoretically be equal to  as there are 256 values of the information source in red, green, blue, and green colours of the image with the same probability.

Entropy values are:

Image	Entropy
Original image	8
Encrypted XOR image	7.99
Decrypted XOR image	7.99
Encrypted XNOR image	7.55
Decrypted XNOR image	7.55

 

6.2.5.  TIME TAKEN FOR ENCRYPTION AND DECRYPTION OF AN IMAGE

With XOR operation: The time taken to encrypt the image is 0.0 sec and time taken to decrypt the image is 3.9375 sec.

With XNOR operation: The time taken to encrypt the image is 0.0 sec and time taken to decrypt the image is 2.828125

sec.

 

6.2.6.  COMPARISON Srushti and Gor (2022)

The table shows the comparison of the results of encryption process done using Laplace transformation with LFSR and RSA with LFSR:

Key Generation	Laplace Transform & LFSR		RSA & LFSR
Key Operation	With XOR operation	With XNOR operation	With XOR operation
Image type	Input image: .jpg Encrypted image: .png Decrypted Image: .png	Input image: .jpg Encrypted image: .png Decrypted Image: .png	Input image: .jpg Encrypted image: .png Decrypted Image:.png
Visual Testing	98.59 %	91.36%	99.78%
NPCR	100 %	100 %	100 %
MSE	4096	0
PSNR	40.96 dB	0 dB
UACI	40.96 %	0 %	78.12 %
Entropy	7.99	7.55
Time taken for encryption and decryption process	0.0 sec & 3.9375 sec	0.0 sec & 2.828125sec	0.0 sec & 3.796875 sec
Strength	Laplace Transformation produces a disordered key.   LFSR produces random and secure key.		RSA algorithm produces a strong public key. LFSR produces random and secure key.
Limitation	Randomness of the key depends on which  is to be chosen for Laplace Transformation.     Key generation by LFSR depends on the primitive polynomial.		Strength of algorithm depends on the selection of the prime numbers. Key generation by LFSR depends on the primitive polynomial.

 

Here, NPCR, MSE, PSNR and entropy results gives better result for encryption and decryption using XOR between Laplace Transform & LFSR.

NPCR and time taken for encryption and decryption process gives better results for encryption and decryption using XNOR between Laplace Transform & LFSR.

Visual testing, NPCR and UACI gives better results for encryption and decryption using XOR between RSA & LFSR.

Thus, using XOR between Laplace Transform & LFSR gives better results for encryption and decryption process while XNOR between Laplace Transform & LFSR gives the worst results.

 

7. CONCLUSION

The key utilized for image encryption and decryption in this paper is produced using a Laplace transform and Linear Feedback Shift Register (LFSR). The suggested approach is extremely sensitive to the LFSR's initial state. A Laplace transform generates the first key, then LFSR uses the first key to generate the second key. Then both keys are XORed and XNORed together to produce a strong key, which is the final key. As a result, the hacker will have a tough time guessing that key. As a result, if the wrong key is used, the image will be radically different.

The results show original and encrypted image is highly uncorrelated and perceptually different. Laplace transform uses more controlled parameters as compared to another algorithms, which enhances the data security. The result has been proven using PYTHON that it is efficient and secure.

Compression between RSA with LFSR is done that shows that using XOR between Laplace Transform & LFSR gives better results for encryption and decryption process.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Anandkumar, S. (2015). Image Cryptography Using Laplace Transform Algorithm in Network Security. International Journal of Computer Science & Engineering Technology, 5(9), 326-330.

Chepuri, S. (2017). An RGB Image Encryption Using Laplace Transform Algorithm. International Journal of Current Trends in Engineering & Research (IJCTER), 3(3), 1-7.

Devi. S. R, Rajarajeswari.V, Thenmozhi. K, RengarajanAmirtharajan and Praveenkumar P. (2018). Henon and LFSR Assisted Key Based Encryption. International Journal of Pure and Applied Mathematics, 119(16), 455-460.

Jain, A., & Sharma, S. (2019). A Novel Digital Image Encryption Method Based on Laplace Transform Algorithm. International Journal of Electronics Engineering.

Jumaa, N. K. (2018). Digital Image Encryption Using AES and Random Number Generator. Iraqi Journal of Electrical and Electronic Engineering, 14(1).

Kapur, V., Paladi, S. T., & Dubbakula, N. (2015). Two Level Image Encryption Using Pseudo Random Number Generators. International Journal of Computer Applications, 115(12), 1-4.

Mondal, B., Sinha, N., & Mandal, T. (2016). A Secure Image Encryption Algorithm Using lfsr and rc4 Key Stream Generator. In Proceedings of 3rd International Conference of Advanced Computing, Networking and Informatics. Springer, New Delhi, 227-237. https://doi.org/10.1007/978-81-322-2538-6_24.

Srushti, G., and Gor, R. (2022). Digital Image Encryption using RSA and LFSR. International Journal of Engineering Science Technologies, 6(4), 1-16. https://doi.org/10.29121/IJOEST.v6.i4.2022.351.