
ON A WAY FOR SOLVING VOLTERRA INTEGRAL EQUATION OF THE SECOND KIND1 Ph. D. in Math Candidate, Department of Computational Mathematics, Baku State University, Baku, Azerbaijan |
|
||
|
|
|||
|
Received 03 January 2022 Accepted 10 February 2022 Published 26 February 2022 Corresponding Author Vusala Nuriyeva, math.lover4baku@gmail.com DOI 10.29121/granthaalayah.v10.i2.2022.4486 Funding: This research
received no specific grant from any funding agency in the public, commercial,
or not-for-profit sectors. Copyright: © 2022 The
Author(s). This is an open access article distributed under the terms of the
Creative Commons Attribution License, which permits unrestricted use, distribution,
and reproduction in any medium, provided the original author and source are
credited.
|
ABSTRACT |
|
|
|
There are many classes’ methods for finding of the
approximately solution of Volterra integral equations of the second kind.
Recently, the numerical methods have been developed for solving the integral
equations of Volterra type, which is associated with the using of computers.
Volterra himself suggested quadrature formula for finding the numerical
solution of integral equation with the variable bounders. By using some
disadvantages of mentioned methods here proposed to use some modifications of
the quadrature formula which have called as the multistep methods with the
fractional step-size. This method has comprised with the known methods and
found some relation between constructed here methods with the hybrid methods.
And also, the advantages of these methods are shown.
Constructed some simple methods with the fractional step-size, which have the
degree p≤4 of the receiving results. Here is applied one of suggested
methods to solve some model problem and receive results, which are
corresponding to theoretical results. |
|
||
|
Keywords: Volterra Integral Equation, Multistep Methods, Stability and Degree,
Multistep Methods of Hybrid Type, Fractional Step-Size 1. INTRODUCTION
As is known the construction and application of integral equations
usually associated with the name as Abel (see for example Polushuk (1977). Extensive information about the emergence of
integral equations with the variable bounders, happened by the intensive work
of Vito Volttera (see for example Polushuk (1977), Volterra (1982), Verlan
and Sizikov (1986), Verjibitskiy (2001), Hairier
et al. (1990), Imanova (2020). For finding the numerical solution of these
equations, Volterra proposed to use quadrature methods and some of
modification. But here consider the construction and application multistep
methods with the new properties to solve Volterra integral equations and also give some comparison constructed here methods
with the known. Let us to consider the following equation. This
equation is called Volterra-Urtuson equation or nonlinear Volter integral
equations. As was noted above Volterra fundamentally investigate the
following linear integral equation. |
|
||
![]() Equation 2
Equation 2
which is known as the linear integral equation of Volterra type. It is obvious that, the
equations ![]() Equation 1
and
Equation 1
and ![]() Equation 2
can be considered as given if the following functions
Equation 2
can be considered as given if the following functions ![]() ,
K (x, s, z) and a(x, s) are known. By
taking this into account, suppose that the given functions are continuous to
totality of arguments and also, they have the continuous
partial derivatives in the domain in which have define the above-mentioned
functions.
,
K (x, s, z) and a(x, s) are known. By
taking this into account, suppose that the given functions are continuous to
totality of arguments and also, they have the continuous
partial derivatives in the domain in which have define the above-mentioned
functions.
2. CONSTRUCTION NUMERICAL METHODS WITH SPECIAL STRUCTURE
For the
construction numerical methods for solving of the equation of Equation 1, let us divide the
segment [![]() to N-equal parts by using the mesh-points
to N-equal parts by using the mesh-points ![]() +h
(i=0, 1, N-1), here 0<h – is the step-size. Let us
denout by the y (
+h
(i=0, 1, N-1), here 0<h – is the step-size. Let us
denout by the y (![]() exact and by the
exact and by the ![]() -approximately values of the solution of the
equations Equation 1 or Equation 2
at the meshpoint
-approximately values of the solution of the
equations Equation 1 or Equation 2
at the meshpoint ![]() (i=0, 1, N). If applied any quadrature method
to solve equation of Equation 1, then that can be written the following (see for
example Hairier
et al. (1990), Imanova (2020)
(i=0, 1, N). If applied any quadrature method
to solve equation of Equation 1, then that can be written the following (see for
example Hairier
et al. (1990), Imanova (2020)
![]()
Here
![]() is the approximatly value for the K (
is the approximatly value for the K (![]() )
)
For
shown disadvantages of this method,let us consider the calculation of the value
![]() :
:
For
the finding some relation between of the values ![]() , here is a comparison of these methods Equation 3 and Equation 4. Noted that,
, here is a comparison of these methods Equation 3 and Equation 4. Noted that, ![]() participating in the equality of Equation 3 and in the equality of Equation 4 is not identical. The value
participating in the equality of Equation 3 and in the equality of Equation 4 is not identical. The value ![]() participated in equality of Equation 3 to correspond the integral:
participated in equality of Equation 3 to correspond the integral:
![]() =
=![]() +
+ ![]() ,
,
But
the method, participated in the equality of Equation 4 to correspond first calculation of
the integral, participated in following equality:
![]()
From
here receive that the values ![]() or
or ![]() are calculated in separate form. To eliminate
the indicated disadvantage have constructed methods, which are free indicated
disadvantage. And in one version have suggested to apply the following method
to solve equation Equation 1
are calculated in separate form. To eliminate
the indicated disadvantage have constructed methods, which are free indicated
disadvantage. And in one version have suggested to apply the following method
to solve equation Equation 1
![]() Equation
5
Equation
5
Prove, that if this method is stable,
then p≤2[k/2] +2, which one and the same with the Dahlquist’s
result (see for example Mehdiyeva
(n.d.), Butcher
(1965). But here prove that
the method with degree p=2k is not unique, which differ from the Dahlquist’s result. For the construction more exact methods
have proposed to use the following method:
![]() Equation 6
Equation 6
(![]() ),
),
and prove that in class of methods Equation 6, there are stable
methods with degree p≤3k+3. Here by using some partible case of the
method Equation 6 constructed simple
methods and have shown the advantage of these methods.
3. CONSTRUCTED THE SIMPLE METHODS WITH HIGH ORDER OF ACCURACY
Noted, that in Ibrahimov
(1984) has constructed one
step stable method of type Equation 6, which has the order
of accuracy p=6 for k=1 and can be presented as followings:
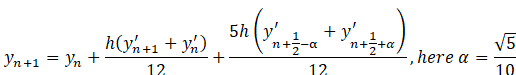
Noted that method Equation 6 in more general form
can be written as follows:
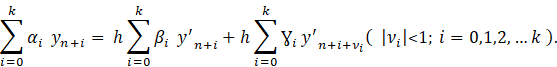
This
method has investigated by many authors (see for example [15]-[20]). By this
method one can be solved ODEs, Volttera integral and Volttera
integro-differential equations.
In application of this method are arises
some difficulties. Therefore, here also to consider the case k=1, it is easy to
understand, that constructed simple methods, which have applied to solve model
problem. For this let us consider to the following method:
![]() ). Equation 7
). Equation 7
It
is known that the coefficient in this formula can be chosen so that degree p=6.
Let’s simplify this method and explore it in two
versions.
First,
let us consider following method:
By choosing the coefficients![]() ,
𝛼 and 𝛽
one can constructed method with the order of accuracy p>2 (as is known the
method with the order accuracy p=2 is the trapezoidal rule, which is very
popular) and can be receive from the formula Equation 7 in the case
,
𝛼 and 𝛽
one can constructed method with the order of accuracy p>2 (as is known the
method with the order accuracy p=2 is the trapezoidal rule, which is very
popular) and can be receive from the formula Equation 7 in the case ![]() .
It is known that, by choosing the coefficients
.
It is known that, by choosing the coefficients![]() ,
𝛼 and 𝛽,
one can be constructed by hybrid method with the order of accuracy p=4, but in
this case values of constant 𝛼 and 𝛽
will be irrational and in this case arises some difficulty with the calculation
of the values
,
𝛼 and 𝛽,
one can be constructed by hybrid method with the order of accuracy p=4, but in
this case values of constant 𝛼 and 𝛽
will be irrational and in this case arises some difficulty with the calculation
of the values ![]() and
and![]() .
Therefore, here decided to take the values of 𝛼
and 𝛽-as the rational number. For example, as
the midpoint rule, this can be written as:
.
Therefore, here decided to take the values of 𝛼
and 𝛽-as the rational number. For example, as
the midpoint rule, this can be written as:
But,
noted that the following hybrid method
has the order of accuracy p=3? Noted that
method Equation 9 is explicit, but the
method Equation 10 is implicit. Let us
the unknowns![]() ,
𝛼 and 𝛽
choose so as method Equation 8 will
be having the maximal order of accuracy. For this to consider the following
Taylor series:
,
𝛼 and 𝛽
choose so as method Equation 8 will
be having the maximal order of accuracy. For this to consider the following
Taylor series:
![]() =
=![]() +h𝛼
+h𝛼![]() +
+![]() +
+![]() +…,
+…,
![]() =
=![]() +hβ
+hβ![]() +
+![]() +
+![]() +…
.
+…
.
By using these expressions in the method
of Equation 8 receive, that in order
to the order of the method Equation 8 has the order of
accuracy p=4, the unknowns must satisfy the following system of algebraic
equations:
![]() / (j+1), j=1, 2, 3. Equation
11
/ (j+1), j=1, 2, 3. Equation
11
By solving this nonlinear system, receive
the following solution:
![]() ;
𝛼= (3-
;
𝛼= (3-![]() )/6,
𝛽= (3+
)/6,
𝛽= (3+![]() )/6.
)/6.
If use these values in the formula Equation 8, then we receive the
following method:
which has the order of the accuracy p=4.
It is not difficult to prove, that the
above received solution of the system nonlinear equations Equation 11 is unique. Therefore
method Equation 12 is also unique. But
method of type Equation 10 is not unique. The
following method is also having type of Equation 10
Methods Equation 10 and Equation 13 different from the
method Equation 12 that in the methods Equation 10 and Equation 13 has used the hybrid
points of the rational type, but in the method Equation 12 have used hybrid
points of the irrational type. Noted that, methods Equation 10 and Equation 13 have the degree p=3.
It is easy to understand, that to
calculation of the values ![]() and
and ![]() is not easy, so as 𝛼 and 𝛽 are the irrational numbers.
Therefore some scientists suggested using the values with type
is not easy, so as 𝛼 and 𝛽 are the irrational numbers.
Therefore some scientists suggested using the values with type ![]() ,
here m and l are the rational numbers. The methods Equation 9 and Equation 10 are of this type. And
now let us show that for using values like
,
here m and l are the rational numbers. The methods Equation 9 and Equation 10 are of this type. And
now let us show that for using values like![]() ,
can be use the value
,
can be use the value ![]() ,
which can be calculated by fractional step size h/m. Methods Equation 9 and Equation 10 are the methods with
fructional step size. Let us consider application them to solving some problem.
It is obvious that for the application to solve some problem it is necessary to
construct some methods for calculation of the walk
,
which can be calculated by fractional step size h/m. Methods Equation 9 and Equation 10 are the methods with
fructional step size. Let us consider application them to solving some problem.
It is obvious that for the application to solve some problem it is necessary to
construct some methods for calculation of the walk ![]() .
By taking into account that the transaction error for
this method can be presented as O (
.
By taking into account that the transaction error for
this method can be presented as O (![]() ).
It follows from here, that the value
).
It follows from here, that the value ![]() must be calculated with the local transaction
error O (
must be calculated with the local transaction
error O (![]() ).
In this case method Equation 9 can be using in the
following form:
).
In this case method Equation 9 can be using in the
following form:
![]()
![]()
Here has used the explicit Euler method.
To obtain more accurate calculations, one could use the implicit Euler method.
And now let us consider to application of using method Equation 10 one must use more
accurately methods. If take into account that the
order of the accurate for the method can be written as: p=3, then receive that
constructed methods for calculation of value the ![]() must had the accuracy p≥2. Hence for
calculation of the value
must had the accuracy p≥2. Hence for
calculation of the value ![]() one can be used the method Equation 9 or the trapezoidal
rule. Thus, there have shown, that the methods with the fractional step-size
have some advantages.
one can be used the method Equation 9 or the trapezoidal
rule. Thus, there have shown, that the methods with the fractional step-size
have some advantages.
For the illustration of above mention
let’s consider using the following way:
Here we have used the values, calculated
by the methods Equation 10 and Equation 13. It is clear, that by
using methods Equation 14 one can be calculated
the approximately values of our problems at the mesh point ![]() .
It is easy to understand, that the values of the solution of our problems
calculated by the method Equation 14 will be more exact,
than the values, calculated by the methods Equation 10 and Equation 13. By taking into the
account the local transaction error of the methods Equation 10, Equation 13 and Equation 14 we receive, that
methods Equation 10 and Equation 13 have the degree p=3,
but the method Equation 14 will have the degree
p=4. It is obvious, that method Equation 14 is more exact. Let us
note that the methods Equation 10 and Equation 13 can be taken as the
symmetric methods. Therefore, above constructed methods can be taken as the
bilateral methods. It follows from here, that by using methods Equation 10 and Equation 13 one can be defining
the interval in which located the exact values of the solution considering
problem, which is very basic question in solving practical problems.
.
It is easy to understand, that the values of the solution of our problems
calculated by the method Equation 14 will be more exact,
than the values, calculated by the methods Equation 10 and Equation 13. By taking into the
account the local transaction error of the methods Equation 10, Equation 13 and Equation 14 we receive, that
methods Equation 10 and Equation 13 have the degree p=3,
but the method Equation 14 will have the degree
p=4. It is obvious, that method Equation 14 is more exact. Let us
note that the methods Equation 10 and Equation 13 can be taken as the
symmetric methods. Therefore, above constructed methods can be taken as the
bilateral methods. It follows from here, that by using methods Equation 10 and Equation 13 one can be defining
the interval in which located the exact values of the solution considering
problem, which is very basic question in solving practical problems.
4. NUMERICAL RESULTS
For the illustration above received
theoretical results, let us consider applications of the methods Equation 10, Equation 13, Equation 14 to following Volterra
integral equation of the second kind:
the
exact solution of the equation equals
![]()
|
Table 1 The Errors of Methods For |
||||||
|
h=0.1 |
h=0.05 |
|||||
|
|
For
the Equation
10 |
For
the Equation 13 |
For
the Equation 14 |
For
the Equation 10 |
For
the Equation 13 |
For
the Equation 14 |
|
0.1 |
4.39E-7 |
4.42E-7 |
1.47E-9 |
5.49E-8 |
5.52E-8 |
9.18E-11 |
|
0.3 |
1.19E-6 |
1.20E-6 |
3.99E-9 |
1.49E-7 |
1.50E-7 |
2.49E-10 |
|
0.5 |
1.82E-6 |
1.83E-6 |
6.07E-9 |
2.27E-7 |
2.28E-7 |
3.79E-10 |
|
0.8 |
2.54E-6 |
2.56E-6 |
8.50E-9 |
3.18E-7 |
3.19E-7 |
5.31E-10 |
|
1 |
2.92E-6 |
2.94E-6 |
9.75E-9 |
3.65E-7 |
3.66E-7 |
6.09E-10 |
By
using the values ![]() receive
that, this solution of our problem will be decreasing. Therefore, in the
following table located the values of our problem Equation 15, calculated by the methods Equation 10, Equation 13 and Equation 14.
receive
that, this solution of our problem will be decreasing. Therefore, in the
following table located the values of our problem Equation 15, calculated by the methods Equation 10, Equation 13 and Equation 14.
|
Table 2 The
Errors of Methods For |
||||||
|
h=0.1 |
h=0.05 |
|||||
|
|
For
the Equation 10 |
For
the Equation 13 |
For
the Equation 14 |
For
the Equation 10 |
For
the Equation 13 |
For
the Equation 14 |
|
0.1 |
4.88E-7 |
4.85E-7 |
1.62E-09 |
6.09E-08 |
6.07E-8 |
1.01E-10 |
|
0.3 |
1.62E-6 |
1.63E-6 |
5.39E-09 |
2.03E-07 |
2.02E-7 |
3.37E-10 |
|
0.5 |
3.01E-6 |
2.99E-06 |
1.00E-08 |
3.76E-07 |
3.75E-07 |
6.26E-10 |
|
0.8 |
5.69E-06 |
5.65E-06 |
1.89E-08 |
7.10E-07 |
7.07E-07 |
1.18E-09 |
|
1 |
7.98E-6 |
7.93E-06 |
2.65E-08 |
9.96E-07 |
9.93E-07 |
1.66E-09 |
By
the comparison results, located in the table Table 1 and Table 2 receive, that if the solution,
investigated problem Equation 15 is increasing in this case the
approximately value is also increase to corresponding exact values.
|
Table 3 The
Errors of Methods For |
||||||
|
h=0.1 |
h=0.05 |
|||||
|
|
For
the Equation 10 |
For
the Equation 13 |
For
the Equation 14 |
For
the Equation 10 |
For
the Equation 13 |
For
the Equation 14 |
|
0.1 |
0.0002 |
0.0003 |
3.77E-06 |
2.82E-05 |
2.87E-05 |
2.37E-07 |
|
0.3 |
0.0004 |
0.0005 |
7.44E-06 |
5.56E-05 |
5.66E-05 |
4.67E-07 |
|
0.5 |
0.0005 |
0.0006 |
8.79E-06 |
6.57E-05 |
6.68E-05 |
5.52E-07 |
|
0.8 |
0.0005 |
0.0006 |
9.40E-06 |
7.02E-05 |
7.14E-05 |
5.90E-07 |
|
1 |
0.0005 |
0.0006 |
9.52E-06 |
7.11E-05 |
7.23E-05 |
5.97E-07 |
For
the receiving more exact compare the values, calculated by the methods Equation 10, Equation 13, Equation 14 for ⋋=-5 and for h=0.1 and h=0.05 in the Table 3 we have located the values,
calculated by above mentioned methods.
|
Table 4 The
Errors of Methods For |
||||||
|
h=0.1 |
h=0.05 |
|||||
|
|
For
the Equation 10 |
For
the Equation 13 |
For
the Equation 14 |
For
the Equation 10 |
For
the Equation 13 |
For
the Equation 14 |
|
0.1 |
0.0003 |
0.0003 |
6.22E-06 |
4.72E-05 |
4.64E-05 |
3.90E-07 |
|
0.3 |
0.002 |
0.0019 |
3.33E-05 |
0.0002 |
0.0002 |
2.09E-06 |
|
0.5 |
0.0065 |
0.0063 |
0.00018 |
0.0008 |
0.0008 |
6.72E-06 |
|
0.8 |
0.0313 |
0.0302 |
0.00051 |
0.0039 |
0.0038 |
3.22E-05 |
|
1 |
0.0861 |
0.0833 |
0.00141 |
0.0107 |
0.0105 |
8.87E-05 |
By
continioing the above described tables in table Table 4 have used values, calculated with
the application above mentioned methods, receive that results located in all
the tables are corresponding to the theoretical results.
5. CONCLUSION
One of the well-researched numerical methods is the
multistep method with constant coefficients. Recent time there is some
modification of this method as the multistep advanced method or multistep
hybrid methods. One of the disadvantages of these methods is the calculation
the values of the solution of the investigated problem at the irrational mesh
points. To construct a method freed from the specified flaw, here has
recommended replacing the values of ![]()
![]() with the rational number and have shown that,
in this case how one can be modified of the known for methods for the
calculation of the values
with the rational number and have shown that,
in this case how one can be modified of the known for methods for the
calculation of the values![]() .
In this case we receive the fractional step method. The well-known
representatives of these methods are the midpoint rule. As shown in the text to
construct suitable methods for calculating values of the solution our problem
at the fractional steps is not difficult. Note that, the numerical methods with
fractional steps have investigated by academician Yanenko.
But the way, which have presented here to construct the methods with the
fractional step-size differ from above mentioned methods in that this scheme is
very simple. Noted, that the stable hybrid methods are more exact than the
stable methods with fractional step-size. As was noted above by using the
results, receiving by the symmetrical methods one can be locate the exact
values of the solution of solving problem. Given the specified properties of
these methods one can be increase the order of accuracy the values, calculated
by the linear combination of these methods. This can be confirmed by the
results of solving our example. We believe that this method will find its
followers.
.
In this case we receive the fractional step method. The well-known
representatives of these methods are the midpoint rule. As shown in the text to
construct suitable methods for calculating values of the solution our problem
at the fractional steps is not difficult. Note that, the numerical methods with
fractional steps have investigated by academician Yanenko.
But the way, which have presented here to construct the methods with the
fractional step-size differ from above mentioned methods in that this scheme is
very simple. Noted, that the stable hybrid methods are more exact than the
stable methods with fractional step-size. As was noted above by using the
results, receiving by the symmetrical methods one can be locate the exact
values of the solution of solving problem. Given the specified properties of
these methods one can be increase the order of accuracy the values, calculated
by the linear combination of these methods. This can be confirmed by the
results of solving our example. We believe that this method will find its
followers.
ACNOWLEDGMENTS
The author expresses thank to the academician Medieval Galina Yuryevna for her suggestion to investigate to the computational aspects of our problem.
REFERENCES
ButcherJ.C. (1965) A modified multistep method for the numerical integration of ordinary differential equations. J. Assoc. Comput. Math., v.12, pp. 124-135. Retrieved from https://doi.org/10.1145/321250.321261
Gear C.S., (1965) Hybrid methods for initial value problems in ordinary differential equations, Algorithm IS, J. Number. Anal. v. 2, pp. 69-86. Retrieved from https://doi.org/10.1137/0702006
Hairier E., Norsett S.P., Wanner G. (1990) Solving ordinary differential equations. (Russian) М., Mir, Retrieved from https://doi.org/10.1007/978-3-662-09947-6
Ibrahimov V.R. ; Imanova
M.N. (2021) Multistep methods of the hybrid type and their application to solve the second kind
Volterra integral equation,
Symmetry 6 13. Retrieved from https://doi.org/10.3390/sym13061087
IbrahimovV.R. (1984) Convergence of the predictor-corrector methods, Godishnik na Vischite uchebzaved. Applied Mathematics, Sofia Boolgaria, pages 187-197
Imanova M.N. (2020) On some comparison of Computing Indefinite integrals with the solution of the initial-value problem for ODE, WSEAS Transactions on Mathematics, 19.19. Retrieved from https://doi.org/10.37394/23206.2020.19.19
Imanova M.N. (2020) On the comparison of Gauss and Hybrid methods and their application to calculation of definite integrals, MMCTSE, Journal of Physics; Conference Series, DOI 10.1088/1742-6596/1742-6596/1564/1/012019, 1564(2020)012019. Retrieved from https://doi.org/10.1088/1742-6596/1564/1/012019
Mehdiyeva G.Yu. (n.d.) ; Ibrahimov V.R On the Computation of Double Integrals by Using Some Connection Between The Wave Equation and The System Of ODE. Retrieved from https://www.researchgate.net/profile/Vagif-Ibrahimov/publication/350755242_On_The_Computation_Of_Double_Integrals_By_Using_Some_Connection_Between_The_Wave_Equation_And_The_System_Of_ODE/links/607019f44585150fe993e059/On-The-Computation-Of-Double-Integrals-By-Using-Some-Connection-Between-The-Wave-Equation-And-The-System-Of-ODE.pdf
Mehdiyeva G.Yu. ; Ibrahimov V.R. ; Imanova M.N. (2019) On the construction of the advanced Hybrid Methods and application to solving Volterra Integral Equation, WSEAS Weak transactions on systems and control, V.14.
Mehdiyeva G.Yu. ; Ibrahimov V.R.;X.-G.Yue, M.K.A.Kaabar, S.Noeiaghdam, D.A.Juraev, (2021)Novel symmetric mathematical problems, international journal of circuits, Systems and signal processing 15 1545-1557. Retrieved from https://doi.org/10.46300/9106.2021.15.167
Polushuk E.M. (1977), Vito Volterra, Nauka, Leningrad, ,114 p.
Verjibitskiy V.M. (2001), Numerical methods, Moscow, Visshaya Shkola, ,382
Verlan A.F., Sizikov V.S. (1986), Integral equations methods, Naukova Dumka, Kiev, 543 p.
Volterra V. (1982), Theory of functions and of integral and integro-differential equations, Moscow, fiz-mat., literature, 304 p
 This work is licensed under a: Creative Commons Attribution 4.0 International License
This work is licensed under a: Creative Commons Attribution 4.0 International License
© Granthaalayah 2014-2022. All Rights Reserved.