INTRODUCTION

The time under the action of a gravitational field, in different reference frames at rest.

In this analysis, we will use the same principles and methods used for the deduction of current theory.

Let us analyze the principles of the theory of relativity between time in a referential belonging to a gravitational field generated by mass M and another reference for that gravitational field.

THE MODEL

Through analysis of Einstein's relativity, derived from the Schwarzschild metric, it is proposed the change of time between a reference frame A within the gravitational field of mass M, and another C on limit of this gravitational field, given by:

The same of:

Considering a reference frame, A on a surface of a spherical mass M, with the radius R and a reference frame C limit of the action of the gravitational field of the mass M.

Where:

G- Gravitational “constant”.

R – Distance between the reference frame A and the center of the mass M, its radius.

M - Mass.

$C^2$ – Potential energy of light in reference frame A.

$t_{A }$ – Time in reference frame A.

$t_{C }$ – Time in reference frame C.

When the signal reaches C, by the action of the gravitational field generated by mass M we have an energy of the “light” in C, given by:

From Eq. (3.1) considering Eq. (2.1) and Eq. (4.3), we have:

From Eq. (6.1), the time in two different stationary frames is inversely proportional to the square root of the “light” energy in those frames.

As we have “light” energies, different in A and C, so we can consider their potential as the square of the speed of “light”, so we will have:

We are then talking about the space traveled by the “light” in the reference frame C, ${ L}_{C }$ and in reference frame A, $L_{A }$ .

Once again, it turns out that space does not contract.

From Eq. (10.1):

The speed of “light” will then be inversely proportional to the equivalent times of each referential frame.

From Eq. (12.1), we conclude that what is constant is the space traversed by “light” in the equivalent times of all reference frames.

TIME DILATION AND SPACE CONTRATION

TIME DILATION

Let us briefly remember Einstein's proposed "Mirror Method”.

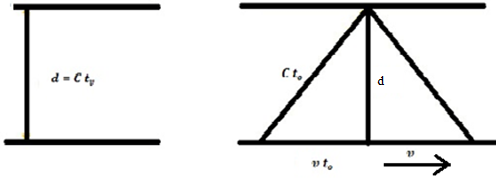
• We are within the moving reference frame.

The conscience we have is that we are stopped

• We are now in a stopped reference looking at the moving reference.

Considering the old Pythagoras theorem, we will have:

Replacing d

The expression that gives us the dilation of time is found in a moving reference v relative to time in the stopped reference frame.

SPACE/OBJECT CONTRACTION

A ; v

We are within the moving reference frame. The conscience we have is that we are stopped.

We are now in the stopped reference frame, looking at the moving reference frame.

The relativity of time will come from:

This value is different from the value found in Eq. (8.2).

If we consider that in this stoped reference frame we observe in motion the lengths change, we will have, from Eq. (15.2), we have:

From Eq. (10.2), we will have

When we are in B and observe the moving object, we conclude that the length of the object is reduced by the coefficient K in relation to the measured length when we are in the frame in motion in the direction of displacement.

As far as I know, this phenomenon has never been observed. There is no news that when we look at a moving object, from a stopped reference frame, it shrinks.

On the other hand, if the moving object shrinks for those who look at it from a stopped frame, this indicates that it shrinks in relation to the length measured at the moment of the moving frame. Since k is introduced as a factor in the second term of the equation, it indicates that the length in the moving frame is constant, since no factor is intruded into the first member of the equation.

Not introducing the K factor in the first member is to assume that the length in the moving reference frame is always constant.

This conclusion drawn from the model proposed by Einstein is contrary to what he proposes.

Einstein proposes precisely the opposite, that in the moving frame, space contracts in the direction of the displacement of the moving frame.

We cannot obtain the time $t_{o }$ of the stopped reference frame and K(v) coefficient of the length contraction in derecction of the displaccement of the moving reference frame.

We are not in a moving reference frame, we are observing from a stopped reference frame

MAKING SENSE?

For the value of K to appear where it was placed, it is because we consider K in the calculation of $t_{o }$ .

From Eq. (18.2):

We are not in any doubt that we are calculating a time in the stopped reference frame $t_{o }$ from a coefficient K in the direction of displacement, in motion.

If we are thinking about changing lengths in a moving frame, then we should consider that K in the moving frame.

After all, what would make sense was the expansion of the objects / space in the reference frames in motion in the direction of this displacement.

THE CONTRACTION OF SPACE AND THE MICHELSON-MORLEY EXPERIENCE

Below we have simplified equipment in order to facilitate the calculation we intend to perform.

Let's consider the arms on the cross, with lengths all the same.

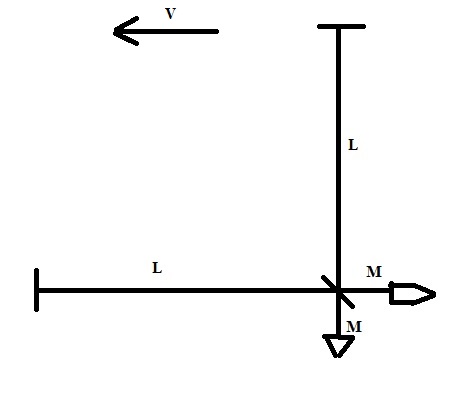
So we will have:

In the direction of travel.

In the direction perpendicular to the displacement.

Here the same type of error is made as in the model proposed by Einstein, or vice versa, the value of K referring to the contraction of the object in the direction of displacement was introduced for the calculation of the time of the reference frame stopped.

Really, the time it would take the light to travel the orthogonal paths would be the same.

But these times, although equal, present a problem that is the dependence on V. This dependence would originate the change in the spectrum of interference in the arrival sensor, which was never suggested.

For V=0

The relativity of the times will come from;

If M=L we have:

Michelson Morley's experience does not verify the expression of time dilation in a moving body, v>0. The higher V is lower the value obtained for the relativity of time $\frac{t_v}{t_0}$ .

If we consider the contraction of space, we question the expression of time dilation, which has long been tested in particle accelerators.

We get the time, $t_{o }$ , in the stopped reference and the K, coefficient of object/space contraction, $L_{v }$ , of a moving reference.

We cannot simultaneously obtain a stopped and moving reference frame.

WHAT IS THE MEANING OF THE EXPRESSION OF TIME DILATION?

The expression is known and already verified in reality in experiments on particle accelerators.

Since our reference frame 0 is at rest and V is the reference frame in motion relative to 0, will we have:

Being:

$t_0$ – The time in our reference frame 0.

$C$ – The speed of light in our frame, which here we now characterize as $C_0$ .

V- Velocity measured in our referential, which we characterize by $V_0$ .

$t_V$ – The time in the reference frame in motion.

In fact what we know is the speed of light and the speed displacement of the moving reference frame measured in our frame. In the expression the terms, time and speed of light are in our refrence frame.

We are looking at the space traveled by the light in our reference frame, $L_0$ , obtained by:

From Eq. (1.4), we have:

In the first term we have a space traveled given by the product of time by the speed of light.

The factor in the second member cannot affect the time in the mobile frame, which would not make sense as this is the unit of your time.

Therefore the dimensionless factor can only be related with the speed of light in the moving reference frame.

In the second member we have the product of time by the velocity which is expressed by. ( $C_0\sqrt{ \frac{{C_0}^2}{{C_0}^2-{V_0}^2} }$ ).

AS $\frac{{C_0}^2}{{C_0}^2-{V_0}^2}$ >1 for v>0, then the velocity $C_0\sqrt{ \frac{{C_0}^2}{{C_0}^2-{V_0}^2} }$ > $C_0$ , the speed measured in the moving frame is greater than the speed of light measured in our frame. This speed can only be the speed of light measured in the moving frame.

If in the first member we have the space traveled by the light in our reference frame $L_0$ , then in the second member we can only have the space traveled by the light in the moving reference frame $L_V$ .

It indicates that the space does not contract and the speed of light in the moving reference frame $C_V$ , is given by:

The same of Eq. (5.4)

Space can not contract.

CONCLUSION

From what, has been analyzed, the principle that the speed of light is constant in all references does not seem right.

The principle to keep in mind is:

The space traveled by light, in the equivalent times of all reference frames, is always constant.

On the other side, it concluded that the measurement of the speed of light, as well as any velocity, is inversely proportional to the respective equivalent times of the reference frames.

There is no contraction of space in the direction of displacement.

We have a different relativity than we've had so far.

INTRODUCTION TO RELATIVITY

Let's look at energy in the view of quantum mechanics.

$E$ – Energy

$h$ - Planck's constant

${\surd }_0-$ Frequency

T - Period

Meeting Planck's constant.

Which confirms the relativity of energy from the theory of traditional relativity.

From Eq.(9.4), ${C_v t}_v$ = ${C_0 t}_0$ , because the space traversed by light is always the same at all equivalent times of all reference frames.

Which indicates that the linear momentum is always the same in all reference frames

When the velocity tends to C then the mass tends to 0, i.e. it turns into energy, which makes perfect sense.