Article Type: Research Article

 

Article Citation: Akhilesh Kumar Dubey, Arun Kumar Rao, and Himanshu Pandey. (2020). BAYESIAN ESTIMATION OF PARAMETERS OF INFLATED GEOMETRIC DISTRIBUTION. International Journal of Research -GRANTHAALAYAH, 8(5), 126-131. https://doi.org/10.29121/granthaalayah.v8.i5.2020.108

 

Received Date: 19 May 2020

 

Accepted Date: 29 May 2020

 

Keywords:

Inflated Geometric Distribution

Joint Beta Prior

Precautionary

Entropy Loss Functions
ABSTRACT

In this paper Bayes estimators of parameters of inflated geometric distribution have been obtained by taking joint beta prior. The loss functions used are squared, precautionary and entropy.

1.     INTRODUCTION

 

Let us consider the inflated geometric distribution whose probability density function is defined by

 

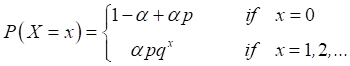                                                                                                                          (1)

 

Where

(Singh, Dixit and Roy, 2015).

We have

 

and             

Thus,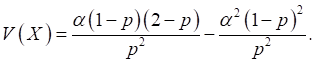         

     

The object of the present paper is to obtain a Bayes estimator of the parameters α and p under different loss functions using a beta prior distribution.

A commonly used loss function is the squared error loss function (SELF)

 

                                                                                                                                                                         (2)

 

The Bayes estimator under the above loss function is the posterior mean, say,is given by

 

                                                                                                                                                                                          (3)

 

Norstrom (1996) introduced an alternative asymmetric precautionary loss function and also presented a general class of precautionary loss functions with quadratic loss function as a special case. A very useful and simple asymmetric precautionary loss function is given as

 

 

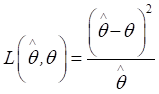           .                                                                                                                                                            (4)

 

The Bayes estimator under precautionary loss function is denoted by  and is obtained by solving the following equation.

 

                                                                                                                                                                               (5)

 

In many practical situations, it appears to be more realistic to express the loss in terms of the ratio . In this case, Calabria and Pulcini (1994) points out that a useful asymmetric loss function is the entropy loss

 

 

Where        and whose minimum occurs at  Also, the loss function  has been used in Dey et al. (1987) and Dey and Liu (1992), in the original form having  Thus  can written be as

 

                                                                                                                                                     (6)

 

The Bayes estimator under entropy loss function is denoted by  and is obtained by solving the following equation

 

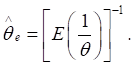                                                                                                                                                                                (7)

     

Since α and p lies between 0 and 1 so that we may take conjugate prior i.e., Beta distribution  and  Also α and p are independent then the joint prior is

 

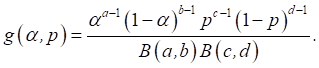                                                                                                                                 (8)

 

2.     BAYESIAN ESTIMATION

 

Let  denote a random sample of size n. Assuming that  denotes the number of observations with value x. The likelihood function can be expressed as below.

 

                                                                                                                                                   (9)        

 

Where       

 

Using binomial expression, L becomes

 

                                                                                                                                                 (10)

 

Under the joint prior as given in (8), the joint posterior of α and p is given by

 

             

        

         

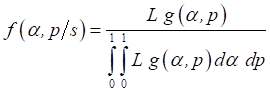
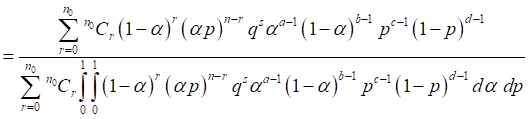
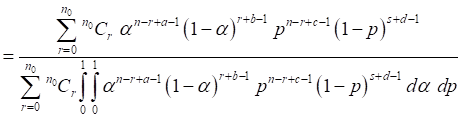
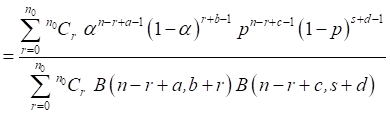                                                                                                              (11)

 

2.1. BAYES ESTIMATORS OF Α

 

      From (11), the marginal posterior of α is given by

 

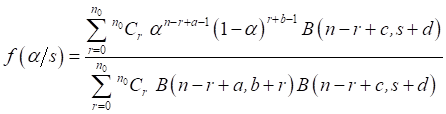                                                                                                (12)

 

Thus the Bayes Estimator of α under squared error loss function is denoted by  and is given by

 

         

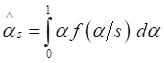
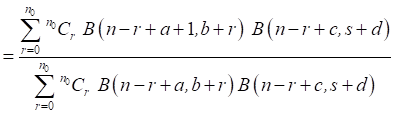                                                                                                            (13)

 

Using (5), Bayes estimator of α under precautionary loss function is obtained as

 

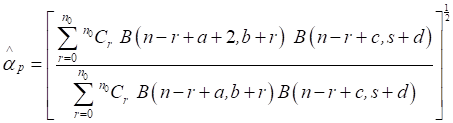                                                                                              (14)

 

The Bayes estimator of α relative to entropy loss function using (7), is obtained as

 

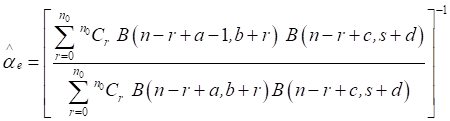                                                                                               (15)

 

 

2.2. BAYES ESTIMATORS OF P

 

From (11), the marginal posterior of p is given by

 

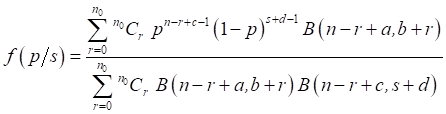                                                                                                (16)

The Bayes Estimator of p under squared error loss function is denoted by  and is given by

          

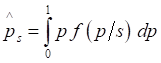
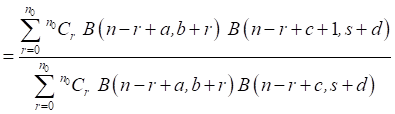                                                                                                            (17)

 

Using (5), Bayes estimator of p under precautionary loss function is obtained as

 

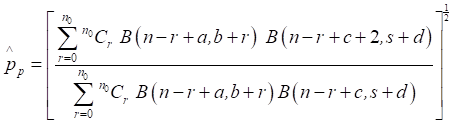                                                                                              (18)

 

The Bayes estimator of p relative to entropy loss function using (7), is obtained as

 

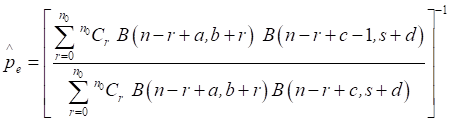                                                                                               (19)

 

3.     CONCLUSION

     

In this paper, we have obtained a number of Bayes estimator of parameters of inflated geometric distribution. In equations (13)-(15) we have obtained the Bayes estimators of α and in equations (17)-(19), the Bayes estimators of p under joint beta prior. In the above equation, it is clear that the Bayes estimators depends upon the parameters of the prior distribution. In this case the risk functions and corresponding Bayes risks does not exist.

 

SOURCES OF FUNDING

 

None.

 

CONFLICT OF INTEREST

 

None.

ACKNOWLEDGMENT

 

None.

 

REFERENCES

 

       [1]      Singh, Dixit and Roy, (2015): Stochastic analysis of infant deaths by age and estimation of parameters. Jour. of Sc. and Tech. 20(1), 1-5.

       [2]      J.G. Norstrom, (1996). The use of precautionary loss functions in risk analysis. IEEE Tran. Rel. Vol. 45, No. 3, 400-403.

       [3]      Calabria, R., and Pulcini, G. (1994): Point estimation under asymmetric loss functions for left truncated exponential samples. Comm. Statist. Theory & Methods, 25 (3), 585-600.

       [4]      D.K. Dey, M. Ghosh and C. Srinivasan (1987): Simultaneous estimation of parameters under entropy loss. Jour. Statist. Plan. And infer., 347-363.

       [5]      D.K. Dey, and Pei-San Liao Liu (1992): On comparison of estimators in a generalized life model. Microelectron. Reliab. 32 (1/2), 207-221.