On Homogeneous Quinary Quadratic Diophantine Equation

 

S. Vidhyalakshmi ¹, M.A. Gopalan ²

 

¹ Assistant Professor, Department of Mathematics, Shrimati Indira Gandhi College, Affiliated to Bharathidasan University, Trichy-620 002, Tamil Nadu, India

² Professor, Department of Mathematics, Shrimati Indira Gandhi College, Affiliated to Bharathidasan University, Trichy-620 002, Tamil Nadu, India

 

1. INTRODUCTION

The theory of Diophantine equations offers a rich variety of fascinating problems. In particular, homogeneous, or non-homogeneous quadratic Diophantine equations with two or more variables have been an interest to mathematicians since antiquity Dickson (1971), Mordell (1969), Andre (1984), Datta and Singh (1938). In this context, one may refer Gopalan and Srividhya (2012), Gopalan et al. (2013), Vijayasankar et al. (2017), Vidhyalakshmi et al. (2018), Adiga  (2020) for different choices of quadratic Diophantine equations with four unknowns. In Anbuselvi and Rani (2017), Anbuselvi and Rani (2018), Gopalan et al. (2013) the quadratic Diophantine equation with five unknowns are analysed for obtaining their non-zero distinct integer solutions. 

This motivated me for finding integer solutions to other choices of quadratic equations with five unknowns. This paper deals with the problem of determining non-zero distinct integer solutions to the quadratic Diophantine equation with five unknowns given by

 

2. METHOD OF ANALYSIS

The second-degree Diophantine equation with five unknowns to be solved is

 

                                                                             Equation 1

 

The process of obtaining different sets of non-zero distinct integer solutions

To Equation 1 is exhibited below:

 

Set 1:

The substitution of the linear transformations

 

                                                                                                          Equation 2

 

in Equation 1 leads to the Pythagorean equation

 

                                                                                                              Equation 3

 

which is satisfied by

 

                                                                      Equation 4

 

 In view of Equation 2, one has

 

                                                                                                      Equation 5

 

Thus, Equation 4 and Equation 5 represent the integer solutions to Equation 1

Set 2:

  Introducing the linear transformations

 

                                                                  Equation 6

 

in Equation 1 it simplifies to the Pythagorean equation

                                                                                                              Equation 7

 

whose solutions may be taken as

 

                                                                    Equation 8

     

In view of Equation 6 the integer solutions to Equation 1 are given by

          

 

Set 3:

Taking

                                                                          Equation 9

                       

in Equation 1 it reduces to

 

                                                                                    Equation 10

 

Treating Equation 10 as a quadratic in z and solving for z, it is seen that  Equation 10 is satisfied by

 

                      

 

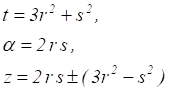
In view of Equation 9 it is seen that the corresponding values of x, y, w   satisfying  Equation 1 are

 

                                      

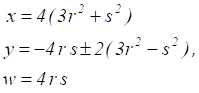
Set 4:

Taking

                                                                        Equation 11

                       

in Equation 1 it reduces to

 

                                                                                     Equation 12

 

Treating Equation 12 as a quadratic in z and solving for z, it is seen that  Equation 12 is satisfied by

                           

 

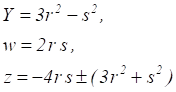
In view of Equation 11 it is seen that the corresponding values of   satisfying  Equation 1 are

                           

 

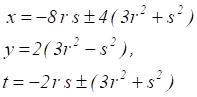
3. CONCLUSION

In this paper, an attempt has been made to obtain non-zero distinct integer solutions to the quadratic Diophantine equation with five unknowns given by  The readers of this paper may search for finding integer solutions to other choices of quadratic Diophantine equations with five or more unknowns.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Adiga, S. (2020). On Bi-Quadratic Equation with Four Unknowns AIP Conference Proceedings 2261. https://aip.scitation.org/doi/abs/10.1063/5.0016866

Anbuselvi, R. Rani, S. J. (2017). Integral Solutions of Quadratic Diophantine Equation With Five Unknowns, IJERD, 13(9), 51-56.

Anbuselvi, R. Rani, S. J. (2018). Integral Solutions of Quadratic Diophantine Equation With Five Unknowns, IJRAT, 6(11), 3327-3329.

Andre, W. (1984). Number Theory : An approach through History, from Hammurapi to Legendre, Birkhauser, Boston.

Datta, B. and Singh, A. N. (1938). History of Hindu Mathematics, Asia Publishing House, Bombay.

Dickson, L. E. (1971). History of Theory of Numbers, Vol.II, American Mathematical Society, New York.

Gopalan, M. A. Sangeetha, V. and Somanath, M. (2013). Integral Point on the Quadratic Equation with Four Unknowns, Diophantus J. Math., 2(1), 47-54.

Gopalan, M. A. Vidhyalakshmi, S. and Lakshmi, K. (2013). On the Non Homogeneous Quadratic Equation, International Journal of Applied Mathematical Sciences, 6(1), 1-6.

Gopalan, M. A. Vidhyalakshmi, S. and Lakshmi, K. (2013). On the Non Homogeneous Quadratic Equation, American Journal of Mathematical Sciences and Applications, 1(1), 77-85.

Gopalan, M. A. Vidhyalakshmi, S. and Premalatha, E. (2013). On Equal Sums Of Like Powers, International Journal of Engineering Research-OnlineA, 6(1), vol 1, issue 3,401-406. http://ijoer.in/Vol%201.3.2013/401-406.pdf

Gopalan, M. A. and Sivakami, S. (2012). Integral Solutions of Quadratic with Four Unknowns, Global Journal of Pure and Applied Mathematics, 8(5), 573-578.

Gopalan, M. A. and Srividhya, G. (2012). On the Diophantine Equation, Impact J. Sci., 6(1), 111-116.

Mordell, L. J. (1969). Diophantine Equations, Academic Press, New York.       

Vidhyalakshmi, S. Gopalan, M. A. Thangam, S. A. (2018). Real and Gaussian Integer Solutions to, GJESR, 5(9), 46-53.

Vijayasankar, A. Gopalan, M. A. Krithika, V. (2017). Observations on, IJRTER, 3(5), 378-381. https://doi.org/10.23883/IJRTER.2017.3238.G5PPT