THE GEOMETRIC THINKING PROCESS OF STUDENTS IN CONSTRUCTING THE CONCEPT OF AREA

 

Markus Palobo ¹, Dwi Juniati ²

 

¹ Student at the State University of Surabaya, Department of Mathematics Education, Universitas Musamus, Indonesia

² Department of Mathematics Education, Universitas Negeri Surabaya, Indonesia

 

1. INTRODUCTION

Geometry is one of the fields of study that has a very wide application in life but tends to be less attractive to students. Students tend to think of geometry as a difficult material. According to research it was found that many students face senior high school geometry classes Gutierrez et al. (1991). can be used in drawing various natural objects and beautiful batik motifs. However, research shows a decrease in students' motivation towards mathematics Gottfried et al. (2001) The material for the flat area can be used, for example, by a contractor in determining the area of a certain area to make it easier to complete a job.

In learning the area of flat shapes, students are generally accustomed to determining the area of flat shapes such as squares, rectangles, parallelograms, triangles, and other flat shapes that are familiar to students. When given a flat shape which is a combination of several types of shapes such as rectangles and triangles as in Figure 1 generally students will be confused, because they only know the area formulas for rectangles and triangle.

Figure 1

                                                                           

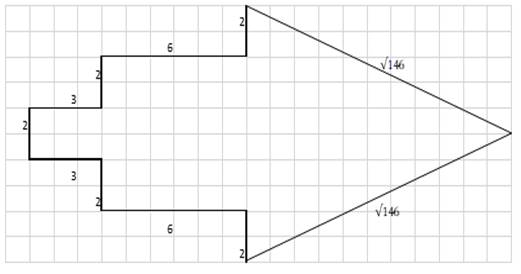
Figure 1 Flat shape combinations of rectangles and triangles

 

Determine the area Flat shapes whose shapes are not familiar become a problem for students because they are used to solving area problems for flat shapes with clear formulas for calculating area. Research shows that students' reasoning has not been maximized in solving the problem of the area of a rectangle Oktaviana and Aini (2021). Students do not realize that in real life, there are so many flat shapes which are a combination of rectangles, triangles, parallelograms, and other shapes that may need to be calculated.

The difficulty of students in determining the area of such flat shapes can be caused because in the learning process students do not understand well the concept of area and more memorize formulas for the area of certain flat shapes, so that when given a flat shape with a model that does not yet have a formula for finding its area, students be difficult. Sulistiani in research found that students tend to memorize the properties of squares and rectangles Sulistiani (2012) Küchemann and Hoyles suggest that in order to solve geometric tasks by reasoning, it is important to consider how to support students to use their spatial intuitive reasoning Küchemann and Hoyles (2006). Achievements abilities mathematically mastered by students have differences, especially in mathematical reasoning abilities which can be seen from each category of students Astuti and Sariningsih (2018) So that each student has the characteristics of reasoning abilities in working on mathematical material, especially on quadrilateral material. The difficulty of students learning geometry occurs, among others, on the subject of quadrilaterals. Sunismi stated that one of the most difficult topics for students to understand is quadrilaterals Sunismi (2001) Furthermore, reported that there are still students who have difficulty in expressing the meaning of flat shapes and the similar characteristics between flat shapes Nu’man (2006)

One of the factors causing the low achievement and interest in learning geometry so far, one of which is caused by the learning carried out by teachers who are still conventional. Schoenfeld stated that conventional mathematics learning resulted in students only memorizing and working procedurally and understanding mathematics without reasoning Sulistiani (2012) It is important for educators to try various learning models so that students' geometric reasoning can be achieved because the ability of educators in the practice of learning greatly affects the learning process of students. Hiebert and Grouws reveal that there is still much to be learned about the interrelationships between teacher practice and student learning. A strong theory practice teacher instructional thus, one of our future tasks is to work with issues such as the influence of different teaching instructions by teachers on decision making, production of conjectures, and processes of evidence construction Hiebert and Grouws (2007) One way to help students determine the area of a rectangular flat shape is to use the help of a checkerboard for class VII students with the concept that a flat rectangular shape with a side length of 1 (one) unit length is 1 (one) unit area Hastoro  (2012) Therefore, in this study, worksheets will be given to students to see students' geometric thinking processes in determining the area of flat shapes, namely squares, rectangles, and triangles. During the process of working on the worksheets in groups, it will be observed how to construct knowledge about the area and how to solve contextual problems related to the area.

The research questions that will be answered in this study are as follows: (1) How is the student's geometric thinking process in constructing the formula for the area of a square, rectangle, and triangle? and (2) how is the student's geometric thinking process in solving contextual problems related to the area of the plane?

 

2. MATERIALS AND METHODS

The type of research is descriptive qualitative which aims to describe students' thinking processes in constructing the formula for the area of a flat figure and solving problems related to the area of a flat figure. The research was conducted at SMP PGRI Buntudatu, Toraja. The research subjects were students of class VIII which consisted of 3 classes. The selection of the research object was carried out randomly and 22 students of class VII C were consisting of 11 boys and 11 girls. The research was carried out in two meetings, the first meeting on Monday 9 May 2022 for 3 hours of lessons and the second meeting on Thursday 12 May 2022 for 3 hours of lessons. The main research instrument is the researcher himself and instrument is student worksheets for two meetings. Prepared Student worksheets are using the guided discovery method with a contextual approach, which aims to enable in the worksheet, students to find the concept of the area formula for the area of a flat figure the context of the real problem for students. The first meeting student worksheet on the material for the area of square and rectangular shapes consisting of 4 problems, and the second meeting on the material for the area of triangular shapes consisting of 4 problems. Techniques data collection were carried out by observation and test methods. Observations were made during the learning process in groups to observe how students solve the problems given in the worksheets as well as explanations of student answers during presentations. While the test data obtained from the results of student work on worksheets in groups. the analysis technique carried out applies the Miles and Huberman method which consists of data reduction, data presentation, and drawing conclusions. Data reduction is done by selecting and selecting raw data to be processed and focused to make it more meaningful. The data that is reduced is the student's answer data for each problem which is focused on the students' processes and techniques in solving the given problem. Data that has been reduced for further presentation. The presentation of the data is done so that the data can be organized, arranged in a pattern of relationships, so that it is easy to understand. The data presented in the form of student work data in groups that describe the geometric thinking process of students in building the formula for the area of flat shapes. Researchers draw conclusions from the data that has been collected and then verify these conclusions. Verification is done by reviewing the results of student answers. Conclusion From this research is to answer research questions.

 

3. RESULTS AND DISCUSSIONS

The first meeting of the researcher started the lesson by reminding the students about the material of flat shapes. The researcher gave initial questions to students about the types of flat shapes they knew. In general, students fluently mention the names of flat shapes such as rectangles, squares, and triangles. After a little while waiting for the students' answers, the names of the shapes such as parallelograms and kites were mentioned by a small number of students. Flat shapes such as rhombus, trapezoid, circle are not in the answers given by students. Initial knowledge students' the types of flat shapes, it can be stated that in general Students class VIII has not been able to identify well all types of flat shapes. Even so, because flat shapes, rectangles, squares, and triangles are well known by all students so that they can be continued for learning activities regarding the area of rectangles, squares, and triangles.

The first meeting learning was carried out in the form of discussion, students were divided into four groups consisting of 5-6 heterogeneous students. After explaining to students about the learning objectives, namely so that students can construct their own understanding of the area of rectangles and squares and be able to determine the formula for calculating the area, the researchers then distributed worksheets for each group to be discussed with the guidance of the researchers. In problem 1, students were asked to determine the area of the rectangle ABCD with the help of one-sided rectangles as a unit area.

Figure 2

                                                                          

Figure 2 Problem Rectangle

 

In problem 1, all groups can calculate the area of the rectangle ABCD smoothly. From the results of group work and observations during the discussion, it was found that 3 out of 4 groups counted the number of square boxes that covered the ABCD rectangle by giving each box a number from the beginning until the number 63 was obtained as the area. of the rectangle. Meanwhile, the other group counted the number of squares of one unit length without numbering the squares but only giving points to facilitate the calculations. The following is one of the answers from group 2 which is identical to the other 2 groups.

Figure 3

                                                                          

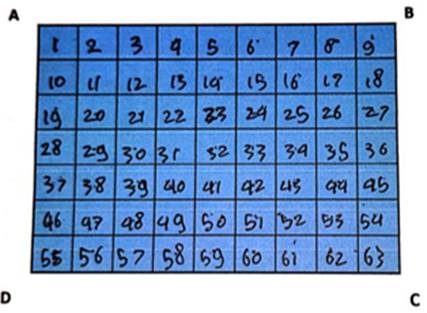
Figure 3 One way for students to calculate the area of the rectangle ABCD

 

Based on the solutions of the four groups, in general it can be found that the students' thinking is still simple, no one has tried to use other methods to calculate the area of the rectangle. It is clear that students have not been able to apply their previous experience of multiplication or repeated addition in calculating the number of squares with one unit length side in rectangle ABCD. In problem 1, the researcher hopes that there is a group that can count the number of squares with a side of one unit length in rectangle ABCD applying multiplication, namely by multiplying the number of columns by the number of rows which is 9 multiplied by 7 or by adding up 9 7 times to obtain the result is 63-unit area. Problem 1 is expected to be able to build students' understanding of the area of a rectangle, namely the multiplication of the dimensions of the long side and the wide side.

In problem 2, the researcher gives the problem of calculating the area of a square way in problem 1, but the help of a square box with a side of one unit of length is made not to cover the entire area of the flat figure.

Figure 4

Figure 4 The problem of the area of a square

 

The researcher made the HIJK square image deliberately so that students can use the concept of multiplication to calculate the area of the square. It is expected that students can use their imagination to imagine the number of squares that cover the empty part of HIJK square. The results of each group's work showed that 2 groups solved problem 2 by adding auxiliary lines so that a square with a side of one unit length covered entire area of the HIJK square to further calculate the number of one-unit squares by writing down the number on each one-unit square as shown in Figure 4 One group directly write down numbers without first adding a guideline, while the other 1 group only uses dots to calculate the area of the HIJK square.

Figure 5

                                                                             

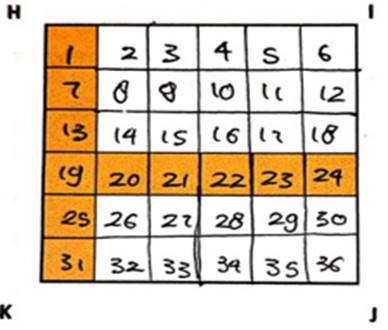
Figure 5 How students calculate the area of a HIJK square

 

In general, it is found that students have not applied multiplication in calculating the area of a HIJK square. Students still count manually the number of all squares of one unit length in the HIJK square shape. Researchers hope that students can use the concept of multiplication to calculate the area of a square in problem 2 has not been achieved. Students are still accustomed to using the manual method in calculating the number of squares with a side of one unit of length. In order to help Students, construct their own formulas for the area of rectangles and squares, then in problem 3, the researcher provides assistance by asking students to re-calculate the area of the rectangle ABCD and square HIJK but not by calculating manually by registering each side square of one unit length that covers the flat shape, but by asking students to use their knowledge of multiplication or repeated addition to obtain area values. With guidance for each group to guide students to recalculate the area of rectangles and squares by applying multiplication. From the results obtained, then ask students to make conclusions about the formula for calculating the area of a rectangle and a square based on solving problems 1 and 2. In this section students have not been able to recall their previous knowledge about the properties of rectangles and squares. With the help of a researcher reminding the long and wide sides of a rectangle and asking students to relate the sides and numbers in problem 1, finally students can write that the formula for the area rectangle is length multiplied by width. Likewise with the problem of the area of a square, by guiding each group, relating to problem 2, they can finally write that the area of a square is the side multiplied by the side.

Although they must be guided and reminded again with the properties of rectangles and squares, the success of students in determining the formula for the area of these shapes gives students their own joy. This means that they actually guide students to construct their own knowledge with guidance and educators. By finding their own, the mathematical concepts learned by students will be more memorable and can last a long time.

The last part of worksheet 1 is a contextual problem related to the area of rectangles and squares. In problem 4, the researcher designs a problem that requires a deep understanding of the breadth in order to solve the problem.

Figure 6

                                                                          

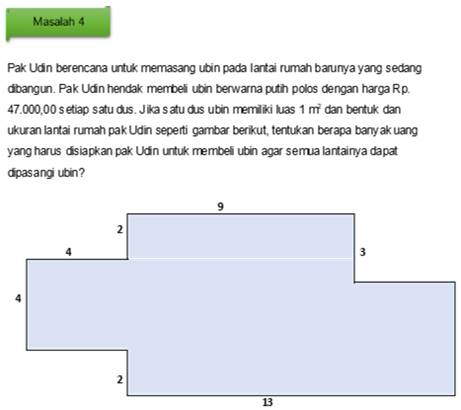
Figure 6 Contextual problems related to the area of rectangles and squares

 

Problem 4 is designed so that students can apply their geometric reasoning to analyse a given image based on a real object, namely the shape of the floor of a house. As Mesquita explains, an external representation of a geometric problem does not in itself enable one to solve a geometric problem but can contribute to the problem solver's definition of the problem structure Mesquita  (1998) One of the ways this happens, according to Mesquita, is when representations lend support to geometric intuition, which in some situations can be very powerful by helping individuals "to understand the relationships between geometric objects. There are several comments from students when looking at problem 4, among others, what are the names of the shapes, what is the formula for the area, we can't calculate the area. From the various comments it can be seen that students are not used to problems that they do not normally encounter. Usually when calculating the area, flat shapes such as rectangles or squares will be presented explicitly so that students can easily calculate the area. When given a picture as in problem 4, which is different from problems 1 and 2, students become confused about how to calculate the area. In problem 4, when students really understand the concept of area, there will no longer be any thoughts of what the formula area is like. Students are expected to go through problem 4 to open their horizons that in everyday life, mathematical knowledge can be used in solving various problems. If it is based on Van Hiele's geometric reasoning level, the VIII grader is still at level I, namely the visualization level Hiele (1986) At this level students recognize and identify certain geometric shapes according to their familiar appearance. However, students did not understand the geometric properties of shapes.

In problem 4, the researcher gave guidance to each group to be able to divide the plane figures in problem 4 into several parts, making it easier for them to find the area of each sub-section. From the results of student work four groups divided the shapes into 3 sub-sections. Furthermore, in determining the size of each sub-section figure, it was found that most of the students had not been able to use geometric reasoning. One group even went back to using the help of a square with sides one unit of length to determine the size of each subsection, but it is not yet precise.

Figure 7

                                                                         

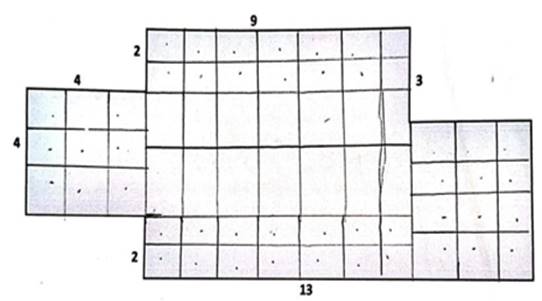
Figure 7 One way of solving problem 4 by students

 

In general, students are still not able to determine the size of the subsections of flat shapes correctly because their understanding of the properties of rectangles and squares is not yet good. It takes students' geometric reasoning to be able to determine the size of the subsections that have not been explicitly to the problem. With the guidance of the researcher, finally students can determine the size of each subsection and calculate its area. From the activity of completing worksheet 1, the researcher found that the students' geometric reasoning in solving each problem was still at the visualization level, not yet available in which students analyse numbers in terms of components and the relationships between components. For example, student analysis can state that the opposite sides of a rectangle are congruent.

The second meeting about the area of a triangle, the researcher hopes that knowledge about the area of a rectangle and square can be used to determine the area of a triangle. The second meeting uses a second worksheet consisting of 4 problems which aims to construct students' knowledge about the area of a triangle. In problem 1 the area of a triangle is given which must be found by using the concept of area as in rectangles and squares.

Figure 8

                                                                          

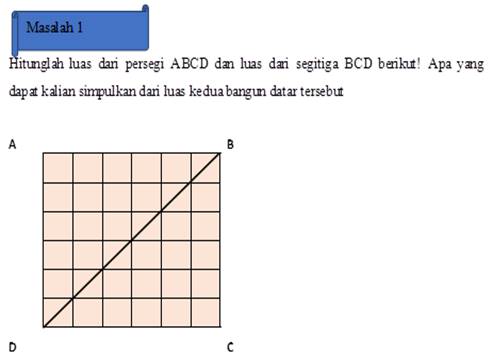
Figure 8 Determining the area of a triangle with the help of a square

 

In problem 1 of worksheet 2, students can calculate the area of a triangle by counting the number of squares on one side of the unit length that cover the area of the triangle BCD. However, if students' geometric reasoning is good, students can clearly see that the triangle is half of a square, so it is enough to calculate the area of the square ABCD, students can determine the area of triangle BCD, which is half of the area of the square.

The results obtained from the work of students in each group obtained that student have difficulty calculating the area of the triangle BCD. The problem they presented was that in the diagonal part of the ABCD square, a square with one side of a unit length is divided into two parts, so that students have difficulty calculating how many squares the total covers the triangle. After the researcher gave guidance by asking to try to pay attention to clearly the size of each square on the diagonal of the square ABCD which is exactly half, so that if you add the second half of the box you will get a square box with a side of one unit length. The results of the calculation of the area of the square and triangle are as shown below.

Figure 9

                                                                         

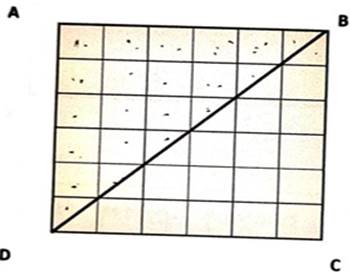
Figure 9 How students calculate the area of a triangle

 

After being guided, 3 groups calculate the area of a triangle BCD by counting the number of squares with one unit length side covering the triangle using the dots to make it easier to count, while other groups immediately counted without the help of dots. In general students have not used their geometric reasoning in seeing the relationship between squares and triangles. The researcher in problem 1 deliberately gave the task to determine the area of the square ABCD so that students could see the relationship between the areas of the two shapes. Students are still at the reasoning stage, which is only able to recognize square and triangle shapes but have not been able to relate the properties of the two shapes. After the researcher gave guidance to each group to compare the area of the square and the area of the triangle, finally the students could conclude that the area of the triangle BCD is half of the area of the square ABCD. To further convince students, the researcher also asked students to look carefully at the picture that clearly the triangle BCD is obtained by dividing the two equal rectangles ABCD. This is done so that students can be applied in solving problem 2.

In problem 2, a rectangle is along with the length and width. In this second problem, students are expected to use the understanding obtained from problem 1 to be able to determine the area of the PRS triangle.

Figure 10

                                                                           

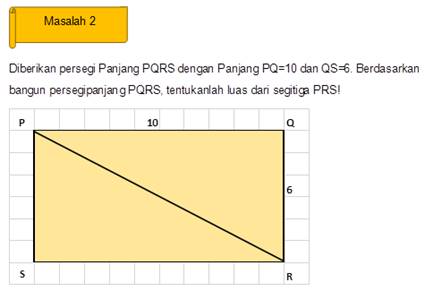
Figure 10 Determining the area of a triangle with the help of a rectangle

 

The results of observations in each group found that students had not used the concepts obtained from problem 1 to solve problem 2. Students were still confused in determining the area of the PRS triangle. The researcher then directed the students to look back at the relationship between the area of the square and the area of the triangle in problem 1. After that asked the students to pay close attention to the picture in problem 2, whether the relationship was in problem 1. After looking carefully, finally the students found that the area of the PRS triangle was half of the area of the rectangle PQRS. From problem 2 it can be seen that students still need more guidance from the teacher to be able to guide them to find the concept of the area of a triangle.

Problems 1 and 2 are designed to help students find the formula area of a triangle. It is hoped that with prior knowledge of the properties of triangles, students can formulate the area of a triangle as half of the product of the base and the height. In problem 3, students still have difficulty writing the formula for the area of a triangle. For example, students still write that the area of a triangle is half times PS times SR. The researcher then directed the students to look again at the PRS triangle, for example. The side PS in the triangle is known as the height of the triangle and the side SR is known as the base of the triangle. With this guidance, finally each group can write the formula for the area of a triangle correctly.

In problem 4 worksheet 2, given a contextual related to the area of rectangles, squares, and triangles. As in worksheet 1, problem 4 aims to enable students to use their geometric reasoning in solving problems that they do not usually encounter in routine learning.

Figure 11

                                                                          

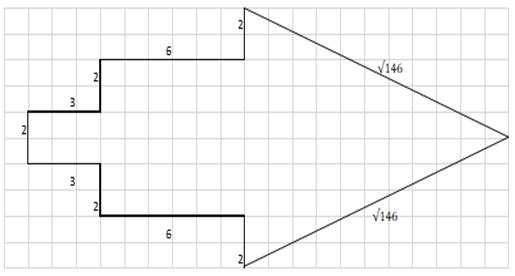
Figure 11 Contextual problems related to the area of a triangle

 

Using previous experience in solving problems on worksheet 1, the four groups of students were able to take the first step in solving problem 4 by dividing the shape into 3 sub-sections. After dividing the shape into 3 sub-sections, the students' difficulty was in determining the size of the triangle, namely, how to determine the height of the triangle. The researcher then reminded the students about the Pythagorean theorem in helping students determine the height of the triangle.

Figure 12

                                                                          

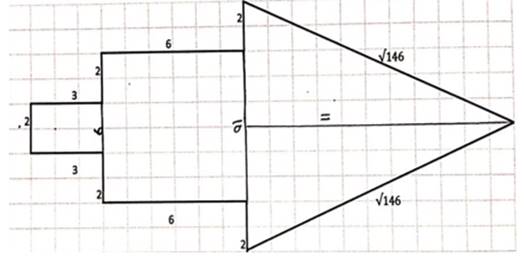
Figure 12 One of the ways students solve problems 4

 

Observations are obtained that there is one group like in the Figure 12 to determine the height of the triangle by counting the number of squares that make up the height of the triangle and obtaining a value of 11. Although it is true, because it is obtained by counting manually, the researcher keeps asking students to prove it using the Pythagorean theorem. The process of solving students in problem 4 is not as difficult as in worksheet 1, indicating that students have been able to use previous experience in solving new problems.

Overall, the first and second learning activities show that students' geometric reasoning when viewed from the Van Hiele level is still limited to level I, namely the visualization level. This is in accordance with several studies that determine the stages of Van Hiele reasoning in the geometry of junior and senior high school students. For example, Halat found that most students in grades K-8 were at level-I reasoning (Visualization) Halat (2007) Likewise, the research of Fuys et al. grade students ninth average and above average abilities, it was found that there were no students who performed geometric reasoning above level-II (Analysis) Fuys et al. (1988)

 

4. CONCLUSIONS AND RECOMMENDATIONS

Based on the results of the study, it was found that the geometric thinking process of students in building knowledge about the concept of area of rectangles, squares and triangles still applies visualization level reasoning, so that difficulties are found in solving the problems given to achieve formula formation. Students still need to be given exclusive guidance and instructions to help construct their knowledge. Students must be reminded again about the properties of rectangles, squares, and triangles so that they are able to determine the formula for the area of these shapes.

In solving contextual problems related to the area of flat rectangles, squares, and triangles, it was found that students still had difficulty determining strategies in determining the area of the given shapes. Students have not been able to use geometric reasoning well in this case applying the properties of rectangles, squares, and triangles in solving contextual problems. Students still have difficulty in determining the size of each sub-section of the flat shape because students' analytical power is still low. The process of solving contextual problems by students still requires guidance from the teacher.

 

ACKNOWLEDGEMENTS

Thank you to the principal of SMP PGRI Buntudatu who has given permission and facilities to carry out this research, as well as the support from lecturers and fellow students of the mathematics education study program at the State University of Surabaya who have always provided support and assistance in completing the writing of this article.

 

REFERENCES

Astuti, P. and Sariningsih, R. (2018). Analysis of the Mathematical Reasoning Ability of Junior High School Students Questions Quadrangle and Triangle Material, JPMI (Jurnal Pembelajaran Matematika Inovatif), 1(4), 807-817. https://doi.org/10.22460/jpmi.v1i4.p807-818

Fuys, D. Geddes, D. and Tischler, R. (1988). The Van Hiele Model of Thinking in Geometry Among Adolescents, Journal for Research in Mathematics Education, 3, 197.

Gottfried, A. Fleming, J. and Gottfried, A. (2001). Continuity of Academic Intrinsic Motivation from Childhood Through Late Adolescence : A Longitudinal Study, 93(1), 3-13. https://doi.org/10.1037/0022-0663.93.1.3

Gutierrez, A. Jaime, A. and Fortune, J. (1991). An Alternative Paradigm To Evaluate the Acquisition of the Van Hiele Levels, 22(3), 237-251. https://doi.org/10.5951/jresematheduc.22.3.0237

Halat, E. (2007). Reform-Based Curriculum & Acquisition of the Levels, Eurasia J. Math. Sci. Technol. Educ., 3(1), 41-49. https://doi.org/10.12973/ejmste/75373

Hastoro, W. (2012). Determining the Area of A Flat Shape With A Checkerboard Students VII.

Hiebert, J. and Grouws, D. (2007). Effects of Classroom Mathematics Teaching on Students Learningin FK Lester (Ed.). Charlotte, NC : Information Age Publishing. 

Hiele, P. V. (1986). Structure and Insight : A Theory of Mathematics Education. New York : Academic Press.

Küchemann, D. and Hoyles, C. (2006). Influences on Students' Mathematical Reasoning and Patterns in Its Development : Insights from A Longitudinal Study With Particular Reference to Geometry, International Journal of Science and Mathematics Education, 4(4), 581-608. https://doi.org/10.1007/s10763-006-9039-6

Mesquita, A. (1998). On Conceptual Obstacles Linked With External Representations in Geometry, The Journal of Mathematical Behavior, 17(2), 183-195. https://doi.org/10.1016/S0364-0213(99)80058-5

Nu'man, M. (2006). Embelajaran Berdasarkan Tahap Berpikir Van Hiele Untuk Membantu Pemahaman Konsep Bangun Segiempat Pada Siswa Kelas VII Mts Negeri Malang 1.

Oktaviana, V. and Aini, I. (2021). Deskripsi Kemampuan Penalaran Matematis Siswa SMP Kelas VII, Jurnal Pembelajaran Matematika Inovatif, 4(3), 587-600.

Sulistiani, I. (2012). Pembelajaran Luas Daerah Persegi Panjang Berdasarkan Standar Pengajaran National Council of Teachers of Mathematics (NCTM) Untuk Meningkatkan Pemahaman Siswa Kelas III SDN Dinoyo I Malang, Fourier, 1(1), 13-20. https://doi.org/10.14421/fourier.2012.11.11-16

Sunismi, (2001). Diagnosis Kesulitan Siswa SLTP Dalam Memahami Konsep Bangun Segiempat Dan Remidinya, Universitas Negeri Malang.