Original Article

The comprehensive theory of relativity and The effect of force

 

 

1.    INTRODUCTION

The existing expressions of special relativity and general relativity are clear. Special relativity only applies to average velocity, General relativity mainly describes universal gravitation. Many production and living conditions in reality are variable speed, The change in speed is the effect of force. So now based on associated with variable speed, it is necessary to derive the comprehensive theory of relativity and the theory of the Effects of force.

In this paper, according to the fundamental principles of Einstein's theory of relativity Einstein et al. (1935), Einstein (1908), Furthermore the effect of variable speed on spatial displacement is proposed, So the expression of comprehensive relativity was derived. Have also studied the various effects of force, the force effects of variable speed, variable energy, abnormal state, and variable position are expressed, the study of these mechanical problems is related to the previously proposed theory of power dynamics Ma (2023).

In the expression of this theory: () describes the three dimensions vector, () described the four-dimensional vector,() described tensors, () Describe direction ( ) Reverse expression of the time component of a 4-dimensional vector. () Describe the mutual displacement of spatial and temporal components in four-dimensional vectors, () described the average value of the physical quantity. The program representatives of Equations and Formula are represented by <i>.

 

2.    The comprehensive theory of relativity

Many physical quantities vary depending on position and velocity, The derivation of relativity requires the comprehensive introduction of the effects of position and velocity.

 

2.1. The expression of comprehensive relativity

Under conditions of varying speed, the change in position is related to the characteristics of speed, The formula for comprehensive relativity is expressed as follows:

 

 

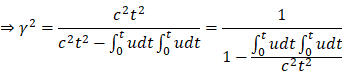
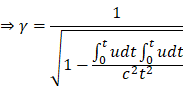
2.2. Simplified expression of the publication of comprehensive relativity theory

According to the characteristics of average speed and variable speed in displacement expression, Introduce variable speed values () related to displacement, The simplified expression of relativity is as follows:

 

 

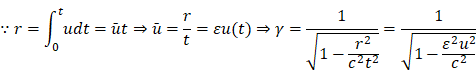
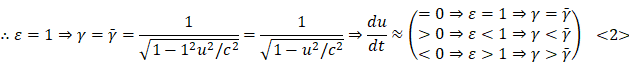
2.3. Energy expression based on comprehensive relativity theory

According to the effect of force on momentum, Force transfers energy in space, Force also has energy transfer in time and object states, so it can always be the combined effect of state reversed four-dimensional force () and four-dimensional position (), The expression of energy is as follows:

 

 

2.4. Relative changes about physical quantities

The calculation principle of the relative reference frame variation of physical quantities: The physical quantity must be a four-dimensional vector, The fourth component of a four-dimensional vector must be variable due to velocity.  According to the principle of power transmission through interaction, Interaction generates power (), The interactive effect changes the four-dimensional component () of the original physical quantity, The rate of change of the four-dimensional component is expressed as (), So the relative changes in the components of four-dimensional component must be expressed according to the principle of conservation (), The physical quantities () about the old coordinate system () generate new physical quantities () about the new coordinate system () due to the transfer of power, Express as follows:

 

 

The expression of the motion state based on the speed () is a motion of the new coordinate system () relative to the old coordinate system ():

 

 

The expression of the motion state based on the speed () is a motion of the old coordinate system () relative to the new coordinate system ():

 

 

2.5. Expressing the relative changes of physical quantities based on tensors

According to the characteristics of the calculation, the relative changes in physical quantities can be introduced into tensor expressions.

The relative variation of the fourth component has characteristics(), The derivation based on tensor expression is as follows:

 

 

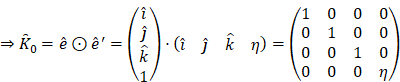
The tensor () expression based on the speed () is a motion of the new coordinate system () relative to the old coordinate system ():

 

 

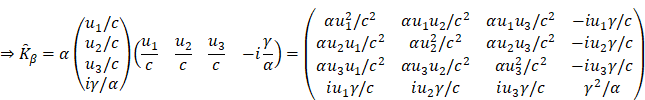
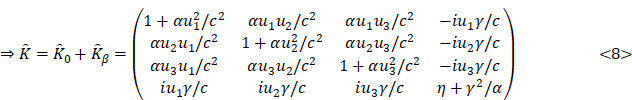
tensor () expression based on the speed () is a motion of the new coordinate system () relative to the old coordinate system ():

    

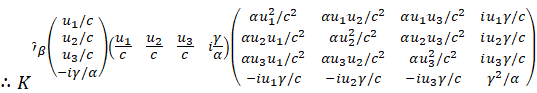
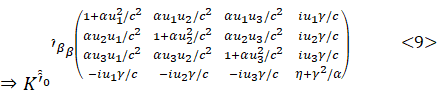
 Calculation of relativistic quantities based on tensor expression:

 

 

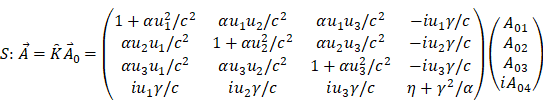
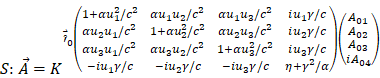
2.6. Time and spatial variations based on the theory of comprehensive relativity

Spatial Variation according to the theory of relativity:

 

 

According to formula <11>, Time Variation according to the theory of relativity:

 

 

Characteristics of Time variation:

 

 

2.7. The calculation method of Differential of relativistic coefficients

The differentiation method of relativistic coefficients () should be calculated according to the characteristics of the application.

According to the specific process of speed change, the differentiation method of relativistic coefficients is as follows:

 

 

 

 

 

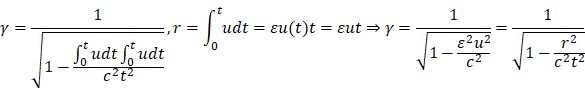
In the general calculation of kinetic energy, the differential method of relativistic coefficients needs to be as follows:

 

 

The differential expression comparison between velocity variation and kinetic energy derivation has the following characteristics:

 

 

3.    The relativistic expression of the effect of force

3.1. The expression of real force based on field source

The real force () is a combination () of basic force () and newborn force ().

Basic force () from Source creation is expressed by three physical quantities: Field strength (), Field source (), and Force load ():

 

 

According to the theory of power flow and variation Ma (2023), Calculate the principle by movement and change of power () generated by Basic force (), So it generated newborn force (), This is related to the velocity () of the field source () and the energy () of the force load (), Express as follows:

 

 

 

In the calculation of newborn force, it is necessary to make calculation expressions according to the characteristics in sequence:

 

 

3.2. Relative force expression based on frame of reference

The four-dimensional vector expression of force ():

 

 

Firstly, assume that the reference frame () is stationary, the velocity of the force load relative to the reference frame is (), The real force can be derived from the expression of momentum:

 

 

 

 

 

 

 

frame () relative to the static reference frame () is (), The momentum () expression of the reference frame, So the expression of the momentum relative to the reference frame () is as follows:

 

 

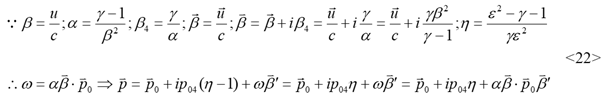
The time based on the static reference frame () is (), The time based on the new reference frame () is (), So the force () expression relative to the reference frame () is as follows:

 

 

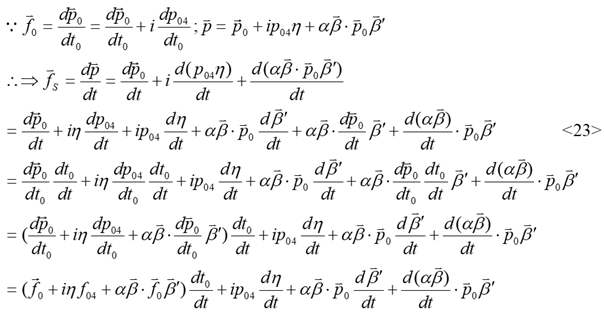
The variation force () of true force () in relativity theory, Generate Class suitability force () in the new reference frame as well, Express as follows：

 

 

 

 

 

 

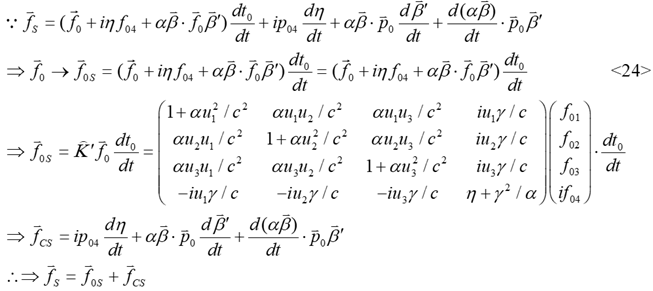
According to the above expression, If the speed () is the static reference frame ()  relative to the reference frame (), The force expression relative to the reference frame () is as follows:

 

 

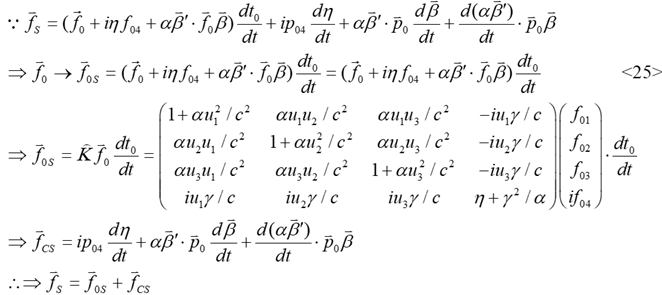
3.3. The energy effect of force

The comprehensive effect of force () is expressed in derivation based on the force effect of momentum (), The expression of acceleration () is also related to force:

 

 

The expression of the total energy () effect of force and the derivation of the total energy position ():

 

In the action of force, the object receiving force undergoes a change in energy in its state, So the change in state energy is the relative change () between total energy and kinetic energy, The expression of abnormal energy ()  is as follows:

 

 

Kinetic energy () is the effect of velocity, so there is a correlation between kinetic energy and the average relative coefficient (), The force effect of kinetic energy is expressed as follows:

 

 

According to the above expression, the effect of force on energy is divided into three categories:

 

 

4.    The effect of force on space

The basic principle of spatiotemporal special effects: Time and space are fundamentally flat, If there is a change, it is essentially the effect of force, so we need to derive the effect of force on space fundamentally.

 

4.1. The mechanical expression of differential space

A flat space forms a curvature based on the action of force, The position of the bend needs to be expressed according to differentiation, Firstly, assume the physical vector (), This vector is a function () of a physical quantity (), It means introducing smaller multiple differential quantities () to express commonly used differential quantities (), Calculate the true constant () of (),  Express the profound differentiation of physical vectors as follows:

 

 

 

 

 

Differential expression of Vectors () and Scalars () of spatial positions:

 

 

The change in spatial position is the effect of force (), The force effect of space curve () is is expressed as follows:

 

4.2. The action of force makes moving objects feel the curvature of space

The action of force causes a change in the differential of position, The variation() of the differential position of force action is the variation() between the true position() and the uniform velocity position(),  Derive as follows:

 

Experience of curvature() and curvature radius() in space Can be experienced, This is fundamentally the effect of force(), The curvature radius() based on the force effect is as follows:

 

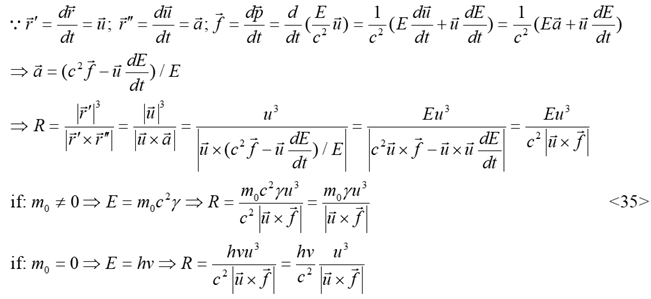
It is necessary to apply curvature vector () in reality, The curvature vector can be derived based on the effect of force (), Derive as follows:

 

 

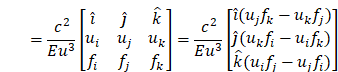
4.3. The effect of universal gravitation on the action of a mass bearing load

Expression of the Universal Gravitational Characteristics basic force () Accepted by a Mass Load:

 

 

According to the theory of power flow, The expression of the newborn force () of universal gravitation of mass under load:

 

 

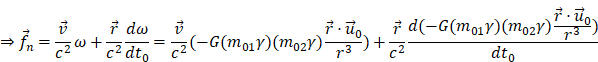
The total gravitational force () of the force load () relative to the gravitational field source () is expressed as follows: Simplified expression of new forces (), The curvature vector() expressed according to formula <36>:

 

 

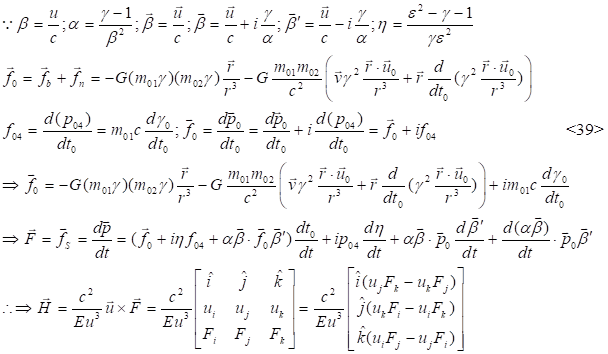
4.4. Expression of Universal Gravitation Accepting a Force Load with Zero Mass

Photons have no mass, Using photons as an example to calculate universal gravitation, Proving the state changes of photons in gravitational space:

 

4.5. Simplified derivation of general relativity

The innovation of general relativity is profound, The expression based on tensors is also very comprehensive, The difficulty of this theory in practical applications lies in the derivation of the curvature tensor () , The root of curvature is the effect of force ()  on motion speed(), So the curvature tensor is defined as follows:

 

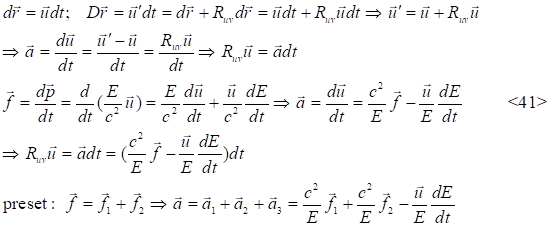
The force () and speed() in expression are already known, The interaction effect between these two vectors and tensors is expressed as follows:

 

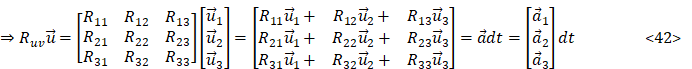
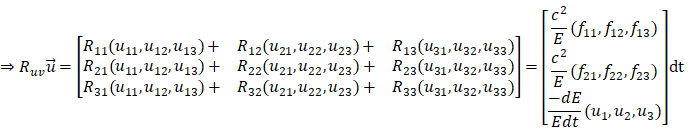
Force and speed must already be known, based on the expression characteristics of vectors and scalars, the curvature tensor can be derived precisely:

 

 

5.    Summary

As is well known, real motion has two characteristics: uniform speed and variable speed. The changes in speed and the curvature of spatial position are related to the effects of force. Therefore, this article establishes a comprehensive theory of relativity and the effects of force. If these two theories are true, they can be effectively applied in reality. According to the fundamental principles of scientific research, these two theories need to be validated through experiments.

  

ACKNOWLEDGMENTS

None.

 

REFERENCES

Einstein, A. (1908). Über Das Relativitätsprinzip Und Die Aus Demselben Gezogenen Folgerungen. Jahrbuch der Radioaktivität und Elektronik, 4, 411–462.

Einstein, A., Podolsky, B., and Rosen, N. (1935). Can Quantum-Mechanical Description of Physical Reality be Considered Complete? Physical Review, 47, 777–780. https://doi.org/10.1103/PhysRev.47.777

Ma, H. (2023). A New Physics Theory About the Kinetic Force Mechanism of Energy Flow. International Journal of Research - GRANTHAALAYAH, 11(1), 115–127. https://doi.org/10.29121/granthaalayah.v11.i1.2023.4988