PIKETTY’S r>g THEORY RECONSIDERED FOR A TRANSITION ECONOMY

 

Yasunori Fujita ¹

 

¹ Keio University, Japan

 

1. INTRODUCTION

A substantial body of theoretical and empirical researches has emerged to explore the relationship between return on capital, economic growth and inequality since Piketty and his coauthors provided a groundbreaking and comprehensive perspective on inequality, by publishing Atkinson, Piketty (2011), Alvaredo et al. (2013), Piketty (2011), Piketty & Saez (2014), Piketty & Zucman (2014),Piketty (2015), Piketty & Saez (2003), Piketty& Saez (2014), Piketty & Zucman (2014) etc.

Bernardo, Martínez, and Stockhammer (2014) lay out a post-Keynesian model to critically examine whether the condition 𝑟>𝑔 (where 𝑟 is the rate of return on capital and 𝑔 is the economic growth rate) necessarily brings about inequality. Their analysis provides a nuanced perspective, questioning the deterministic link between 𝑟>𝑔 and wealth concentration. Jones (2015), on the other hand, by using an overlapping generations model, demonstrates that if 𝑟 and 𝑔 are constant values, degree of wealth inequality in the asset distribution depends on 𝑟−𝑔, and also that if 𝑟 adjusts to balance the supply and demand for capital, this difference converges to the population growth rate.

Mankiw (2015) offers a recalibration of Piketty’s arguments by incorporating considerations such as consumption patterns, procreation, and taxation. His findings suggest that Piketty's pessimistic scenario of an endless and escalating inequality spiral—where the wealth of the capitalist class grows significantly faster than the income of workers—is not consistent with historical evidence. According to Mankiw, 𝑟 would need to exceed 𝑔 by at least seven percentage points annually to produce such an outcome, a condition he argues is far from what has been observed in modern economies.

Fujita (2015) contributes further by developing a theoretical model that distinguishes between real capital (e.g., machinery, buildings) and financial capital (e.g., stocks, bonds) to analyze how 𝑟>𝑔 affects the ratio of capital to income. His analysis elucidates the specific conditions under which the inequality between capital owners and workers is exacerbated, highlighting the role of financialization and institutional factors.

The present paper examines the problem from a different perspective. Specifically, it focuses on an economy consisting of laborers and capitalists, which is transitioning from a barter-based system to a currency-based monetary system and demonstrates that inequality between laborers and capitalists does not increase in the short term, even when 𝑟 > 𝑔 holds.

Structure of this paper is as follows. Section 2 constructs the basic model and section 3 examines the relationship between changes in inequality over time and the difference between 𝑟 and 𝑔. Concluding remarks are made in section 4.

 

2. BASIC MODEL

Let us consider an economy that is in the process of shifting from a barter-based system to a currency-based monetary system. The economy consists of laborers and capitalists, who are assumed to lead self-sufficient lives and establish a joint enterprise to acquire money by selling goods outside their region.

The goods are produced from labor and capital that are offered by laborers and capitalists, respectively, and hence the revenue is distributed completely between them. As for technology, we assume that production is linear with respect to labor and that capital is utilized as a fixed equipment. We also assume that one unit of labor is necessary to produce one unit of goods in each period, for the simplicity of the analysis, and the joint enterprise lasts for t periods.

Under this setup, the profit-maximizing level of production is indeterminate, meaning that production will adjust to the level of demand, which is initially assumed to be D and grows at a rate of g.

Thus, if we let r and C denote interest rate and the capital the capitalist offers at the  beginning of period 1, respectively,  sum of the capital and interest the capitalist receives in period t is (1+r)^tC, and hence sum of the laborer’s revenue over t periods is {1+(1+)+(1+)²+…+(1+)^t-1}D-(1+r)^tC, which reduces to .

 

 

 

 

3. Relationship between inequality over time and difference between r and g

If we let K and Y denote the sum of the capital and interest the capitalist receives in period t and the sum of the laborer’s revenue over t periods, we have   as

                                                                                                 (1)

 

By differentiating (1) with respect to t, we have

,                      (2)

 

which reveals that  holds under the condition of . By solving (2) with respect t, we have t that satisfies (2), t* as

.                                                                                                 (3)

 

Now, we are ready to examine the relationship between inequality over time and difference between r and g.

From (3), we see that there exists no t which satisfies  within the range of t≧0 if .

Since >0, graph of  is depicted as a monotonically increasing curve if , as in Figure 1, which indicates that inequality between laborers and capitalists decreases as Piketty (2014) shows.

 Figure 1

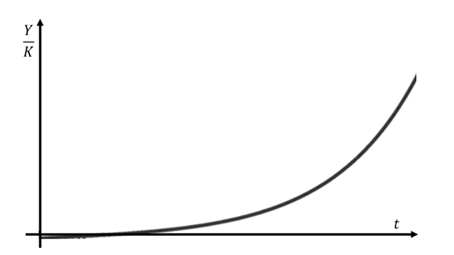
Figure 1 Inequality over time when r<g

 

From (3), we also see that there exists t which satisfies  within the range of t≧0 if .

Since  >0, graph of   is depicted as one peaked convex upward curve if , as in Figure 2, which establishes the following proposition.

 

Proposition:

If the return on capital if r exceeds the growth rate if g, inequality between laborers and capitalists decreases at first and increases afterwards.

 

The proposition is an extended version of Piketty (2014) that claims that inequality between laborers and capitalists increases monotonically.

Figure 2

 

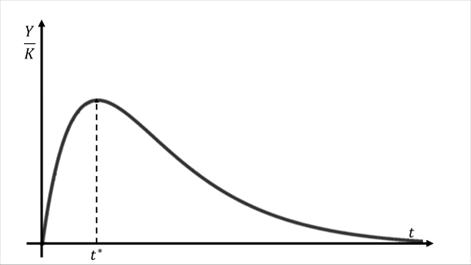
Figure 2 Inequality over time when r>g

 

4. Concluding remarks

The present study theoretically investigated the relationship between changes in inequality over time and the difference between 𝑟 and 𝑔. The results suggest that if r<g, inequality between laborers and capitalists decreases initially but increases afterward.

To enhance the robustness of our findings, it is necessary to examine them within a more general framework that incorporates domestic demand. Additionally, it would be worthwhile to extend the model so that 𝑟 and 𝑔 are determined endogenously. These analyses will be undertaken in our next paper.

Thomas Piketty’s economics has sparked significant controversy. We truly hope this research note will contribute to a better understanding of the complex interplay between capital, growth, and inequality in contemporary economic systems, as highlighted by Thomas Piketty.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

 

 

REFERENCES

Alvaredo, F., Atkinson, A. B., Piketty, T., & Saez, E. (2013). The top 1 Percent in International and Historical Perspective. Journal of Economic Perspectives, 27 (3), 3-20. https://doi.org/10.1257/jep.27.3.3   

Atkinson, A. B., Piketty, T., & Saez, E. (2011). Top Incomes in the Long Run of History. Journal of Economic Literature, 49(1), 3-71. https://doi.org/10.1257/jel.49.1.3 

Bernardo, L., Martínez, J., López, F., & Stockhammer, E. (2014). A Post-Keynesian Response to Piketty's "Fundamental Contradiction of Capitalism." Post Keynesian Economics Study Group, Working Paper (1411).

Fujita, Y. (2015). Missing Equation in Piketty's r-g Theory. Economics and Business Letters, 4 (2), 53-57. https://doi.org/10.17811/ebl.4.2.2015.57-62

Jones, C. (2015). Pareto and Piketty: The Macroeconomics of Top Income and Wealth Inequality. Journal of Economic Perspectives, 29(1), 29-46. https://doi.org/10.1257/jep.29.1.29 

Mankiw, N. G. (2015). Yes, r > g. So what? American Economic Review, 105(5), 43-47. https://doi.org/10.1257/aer.p20151059

Piketty, T. (2011). On the long-run Evolution of Inheritance: France 1820-2050. Quarterly Journal of Economics, 126 (3), 1071-1131. https://doi.org/10.1093/qje/qjr020

Piketty, T. (2014). Capital in the twenty-first century (A. Goldhammer, Trans.). Belknap Press. https://doi.org/10.4159/9780674369542

Piketty, T. (2015). Putting Distribution Back at the Center of Economics: Reflections on Capital in the Twenty-First Century. Journal of Economic Perspectives, 29(1), 67-88. https://doi.org/10.1257/jep.29.1.67

Piketty, T., & Saez, E. (2003). Income Inequality in the United States, 1913-1998. Quarterly Journal of Economics, 118 (1), 1-39. https://doi.org/10.1162/00335530360535135

Piketty, T., & Saez, E. (2014). Inequality in the Long Run. Science, 344(6186), 838-844. https://doi.org/10.1126/science.1251936

Piketty, T., & Zucman, G. (2014). Capital is back: Wealth-Income Ratios in Rich Countries 1700-2010. Quarterly Journal of Economics, 129(3), 1255-1310. https://doi.org/10.1093/qje/qju018