Study on sealing performance of airtight buckle under complex loads

 

Hao Chen ¹, Wenwu Yang ² , Yuhan Tao ³, Xin Li ⁴

 

¹ School of Mechatronic Engineering, Southwest Petroleum University, Chengdu, China

² Doctor, School of Mechatronic Engineering, Southwest Petroleum University, Chengdu, China

³ Sichuan Aerospace, Chengdu, China

⁴ School of Mechatronic Engineering, Southwest Petroleum University, Chengdu, China

 

1. INTRODUCTION

Production tubing is widely used in oil and gas extraction. During the production process, the tubing is subject to complex loads such as internal pressure, external pressure, bending moment, and axial tension, et al. Furthermore, the threaded connection between production tubing is the most critical component in the structure, on account of easy damage or leakage under complex loads Yao (2019), directly impacting the safety of the entire production tubing system, as shown in Figure 1. Therefore, many scholars had conducted researches on the mechanical performance of airtight buckle Chen et al. (2015), Galle et al. (2013), Hamilton et al. (2009).

Figure 1

 

Figure 1 Broken Sealing Surface of Joint

 

Some scholars have attempted to evaluate the mechanical performance of airtight buckle by theoretical methods. Chen et al. (2018) has developed a calculation method for the stress distribution in threaded joints to evaluate the distribution pattern of thread stresses under tension and compression loads. Yu et al. (2022)  has proposed a semi-theoretical and semi-empirical model to analyze the influence of internal pressure and axial force on the sealing performance. Moreover, Yang et al. (2023) has established a sealing performance evaluation model by the Hertz theory and von Mises yield criterion, the influence of the additional torque from sealing interface on the distribution of sealing contact stress and key sealing parameters, including contact width, yield width, average contact stress, and gas sealing capability, is explored. Although theoretical methods can quantitatively investigate the effect of simple loads on the mechanical performance of seal connections, it is also challenging to study the mechanical performance of the joints accurately under complex loading conditions.

Therefore, some scholars have attempted to study the sealing performance of gas-tight seals using the finite element method Cui et al. (2015), Li et al. (2016). The influence of internal pressure on the contact stress and stress in threaded connections is analyzed by Dou et al. (2012), it is revealed that an increase in internal pressure leads to higher von Mises stress and contact stress in the threaded contact area. Yu et al. (2012) studied the effects of axial tension on the contact stress and Mises stress of threaded joints, the results show that a limited axial tensile load has a significant impact on the contact stress at the thread shoulder but a minor effect on the contact stress at the sealing surface. Then, the influence of bending moments on the contact stress of the sealing surface is researched by Wang et al. (2015), the conclusion shows that the contact stress of the seal will decrease exerted by bending load. However, due to the presence of complex loads, such as internal pressure, external pressure, bending moment and axial tension in the working environment of production tubing, considering the mutual influence of these loads can improve the design of threaded joints to enhance safety performance. Therefore, the sealing performance and strength of threaded joints under makeup torque, internal pressure, tension load and compression load is explored by Zhang et al. (2012). The distribution of contact stress along the axial direction of the sealing surface and the stress distribution in the threaded connection is obtained. It was also observed that under these conditions, the compressive performance and joint strength of the threaded connection were higher than that of the pipe. Moreover, tension and compression loads had a detrimental effect on the sealing performance, while internal pressure improved the sealing capability. In addition, Chen et al. (2018) performed the sealing performance of joints under the combined effects of pre-tension, axial force and bending moment, it is obtained that the sealing performance of joints depends on the contact stress between the threads, sealing surfaces and flanges, and the axial tensile loads enhance the sealing load on the threads and weaken the sealing performance of the flanges and sealing surfaces. However, bending moments increase the compressive contact stress on one side and reduce the contact stress and sealing band width on the tensile side of the sealing surfaces. Furthermore, the finite element analysis and experiment is conducted to determine the leakage path between engaged threads under bending moment by Nagata et al. (2020). They found that the sealing performance of the joint is largely influenced by the contact status between the thread crest and root, as well as the contact status of the sealing surfaces.

In present, the combined effects of axial tension, bending moment, internal pressure and external pressure on mechanical property of airtight buckle need further exploration. Currently, there is a lack of literature that comprehensively considers these factors for evaluating the sealing performance. Therefore, this article aims to explore the sealing performance of production tubing with trapezoidal thread connections under complex conditions by the finite element method. The specific arrangement is as follows: in the section 2, a mechanical model of the trapezoidal thread connection is established. The mechanical performance of the joints under simple and complex loads is discussed in the section 3. In the final part, some constructive conclusions are drawn.

 

2. Joint mechanics model

2.1. The theoretical model of contact stress of Joint

In order to simplify calculations, the article converts the makeup torque into the interference fit between the corresponding contact surfaces. The sealing structure between conical surfaces can be simplified as an interference fit of a hollow cylinder. This allows contact stress to be calculated by the theory of thick-walled cylinders in elasticity. The radial interference fit at the sealing surface is shown in Figure 2.

Figure 2

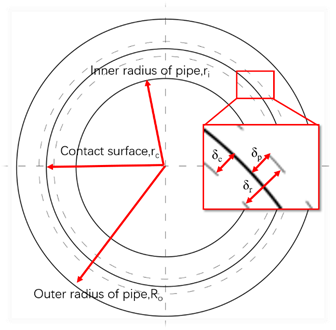
Figure 2 Radial Interference Fit

 

Let the inner radius be denoted as a, the outer radius as b, the internal pressure as , and the external pressure as . The radial displacement at any point on the cylindrical surface can be obtained from the Lame stress formula Xu et al. (2014), as given in equation (1):

 

                                                                     (1)

 

In this equation, v is the Poisson's ratio, E is the elastic modulus (in MPa), a is the inner radius of the cylinder (in mm), b is the outer radius of the cylinder (in mm),  is the internal pressure (in MPa),  is the external pressure (in MPa), and r is the radius (in mm) of any point within the cylinder.

Substituting , , ,  and  into equation (1), the radial contraction of the outer surface of the pipeline can be obtained, as shown in equation (2):

 

                                                                                                      (2)

 

in which,  is the radial contraction of the outer surface of the pipeline (in mm),  is the radius of contact surface (in mm),  is the radial contact stress (in MPa),  is the elastic modulus of the pipeline (in MPa),  is the inner radius of the pipeline (in mm),  is the Poisson's ratio of the pipeline.

 

Due to the fact that the internal pressure acting on the pipe joint can be regarded as the contact stress . When the external pressure on the joint is zero, and , , , , the radial contraction of the inner surface of the joint can be obtained:

 

                                                                                                         (3)

 

where  represents the radial contraction of the joint inner surface (in mm),  is the elastic modulus of the joint (in MPa),  is the outer radius of the joint (in mm), and  is the Poisson's ratio of the joint.

The sum of the absolute values of  and  is equal to the radial interference .

 

                                                                                                                         (4)

 

By substituting equations (2) and (3) into equation (4) and rearranging, the expression for radial contact stress can be obtained as shown in equation (5).

 

                                                                                                (5)

When the joint and pipeline material are the same, the above equation can be simplified as equation (6).

 

                                                                                                                   (6)

 

2.2. Establishment and validation of a finite element model

In order to investigate the sealing performance of oil pipe-joint under complex working conditions, this paper selected a commonly used  inch (73.01mm outer diameter, 61.99mm inner diameter) P110 grade pipeline found in oil fields as the research subject. The thread taper ratio is 1:16 and the connection type is BGT1, as shown in Figure 3. The sealing structure employs a double-cone configuration with a  angle at the shoulder. During the production operational process of oil tubing, they are subjected to internal pressure from the fluid, external pressure caused by the operating environment, axial tension caused by gravitational forces, bending moments due to wellbore trajectory or geological movement and loads resulting from make-up torque at the threaded connections and sealing surfaces. The three-dimensional model and boundary conditions are shown in Figure 4.

Figure 3

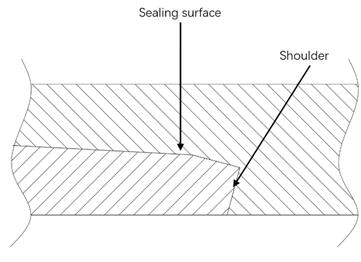
Figure 3 The BGT1 Joint Structure

 

Figure 4

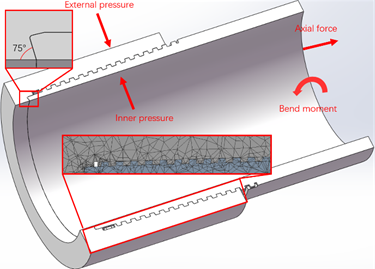
Figure 4 The BGT1 Joint Mechanical Model

 

Due to the fact that the joint is not a standard thick-walled cylinder structure. To prevent interference of the joint structure on the contact stress of the sealing surface, only a radial interference fit is applied at the sealing surface. When the interference amount is 0.01mm, the comparison between the theoretical and numerical values are shown in Figure 5. The theoretical values agree well with the numerical results, which can verify the accuracy of the model.

Figure 5

Figure 5 Model Validation

 

3. Mechanical performance of threaded joints

3.1. Simple loads effect analyses

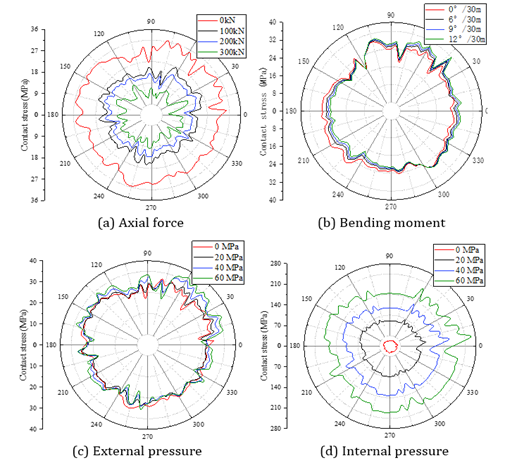
During the production process, oil pipelines are subjected to internal and external pressures from the production environment. Additionally, they experience tensile forces due to their own weight, and bending moments resulting from the curvature of the wellbore trajectory. According to the grouping shown in Table 1, the contact stress distribution on the sealing surface for different kinds of load is illustrated in Figure 6 (a), (b), (c), (d) and (e) are the contact stress on sealing surface under makeup torque, external pressure, bending moment, axial force and internal pressure, respectively. It should be noted that the results in Figure 6 (b), (c), (d) and (e) is also subject to makeup torque. It can be observed that the contact stress on sealing surface under the axial tensile force and internal pressure is different from that under the bending moment and external pressure.

For Figure 6 (a), (b) and (c), the results show that the contact stress on the sealing surface increases gradually along the axis away from the sealing surface. However, when the tensile force and internal pressure reach certain magnitudes, this distribution pattern is reversed, as illustrated in Figure 6 (d) and (e). Therefore, to ensure the accuracy of results and minimize the impact of this characteristic, pressure extraction was conducted on the central nodes of the seal surface for subsequent analysis. The positions highlighted in purple in Figure 7 are utilized for extracting contact stress.

Table 1

Table 1 Loads Combinations
Group number	Internal pressure (MPa)	External pressure (MPa)	Bend moment (°/30m)	Aixal force (kN)	Interfrence amount (mm)
1	0	0	0	0/100/200/300	0.01
2	0	0	0/6/12/18	0	0.01
3	0	0/20/40/60	0	0	0.01
4	0/20/40/60	0	0	0	0.01

 

Figure 6

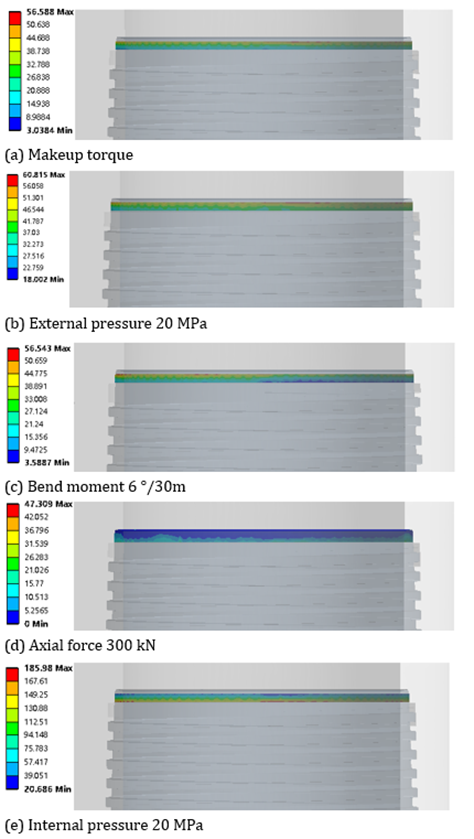
Figure 6 Contact Stress Contour of Sealing Surface

 

Furthermore, contact stress variation occurs along the axial direction, which is attributed to the unique structure of the joint. Unlike a perfect thick-walled cylinder, the joint is a composite structure consisting of conical and cylindrical surfaces.

Figure 7

Figure 7 Positions for Extracting Contact Stress

 

In order to explore the effect of load types on the contact stress of the joint sealing surface, the different load groups are listed in Table 1. The circumferential contact stress of contact surface for different load values is depicted in Figure 8 under the various load groups. Figure 8 (a), (b), (c) and (d) are the circumferential contact stress on sealing surface under axial force, bending moment, external pressure and internal pressure, respectively. It is illustrated from Figure 8 (a) that as the tension on the tubing increases, the contact stress on its sealing surface gradually decreases. The results in Figure 8 (b) revealed that an increase in bending moment results in a gradual decrease in the contact stress on the tension side of the sealing surface, while the contact stress on the compression side gradually increases.

Figure 8  

Figure 8 Circumferential Distribution of Contact Stress on the Sealing Surface

 

The results in Figure 8 (c) indicate that the an increase in external pressure has a minor effect on the contact stress and does not exhibit a clear pattern. That is to say, as the external pressure rises from 0 to 60 MPa, the contact stress at the sealing interface fluctuates within a small range around its initial value. The reasons for this phenomenon can be explained that the radial length between the sealing interface and the external pressure application surface is relatively large. The results in Figure 8 (d) show that the effect of internal pressure on the distribution of contact stress at the sealing surface is highly pronounced, with a significant increase in contact stress as the internal pressure increases.

 

3.2. Complex loads effect analysis

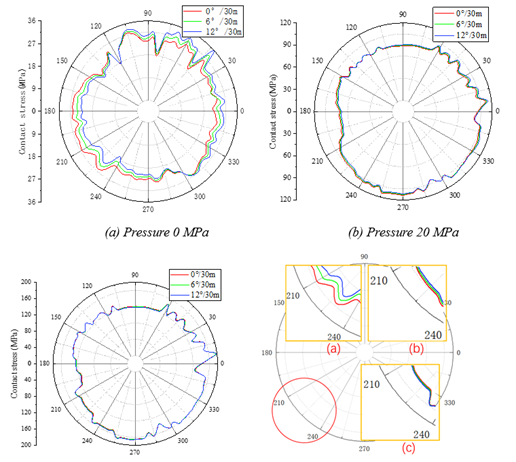
Considering that the actual loads sustained by production columns are often diverse, such as the combined effects of axial tension, bending moment, internal pressure and external pressure on mechanical property of airtight buckle. In this section, it is assumed that internal and external pressure are equal to discuss the combined impacts of axial tension, bending moment and pressure. The combinations of loads are given in Table 2. The circumferential contact stress on the sealing surface for different load values is depicted in Figure 9. Figure 10 and Figure 11. The results in Figure 9 (a), (b) and (c) are derived from groups 1, 2 and 3 in Table 2, respectively. The results in Figure 10 (a), (b) and (c) correspond to groups 4, 5 and 6 in Table 2, respectively. The results in Figure 11 (a), (b) and (c) correspond to groups 7, 8 and 9 in Table 2, respectively. It should be noted that the partial enlargement drawings are shown in Figure 9 (d), 11(d) and 12(d).

Table 2

Table 2 Loads Combinations
Group number	Aixal force(kN)	Internal pressure (MPa)	External pressure (MPa)	Bending moment(°/30m)	Interference amount(mm)
1	0	0	0	0/6/12	0.01
2	0	20	20	0/6/12	0.01
3	0	40	40	0/6/12	0.01
4	100	0	0	0/6/12	0.01
5	100	20	20	0/6/12	0.01
6	100	40	40	0/6/12	0.01
7	200	0	0	0/6/12	0.01
8	200	20	20	0/6/12	0.01
9	200	40	40	0/6/12	0.01

 

  

 

 

 

 

 

 

 

 

Figure 9

Figure 9 Axial Force 200kN

 

Figure 10

Figure 10 Axial Force 100kN

     Figure 11

Figure 11 Axial Force 200kN

 

In Figure 9 (a), Figure 10(a) and Figure 11(a), it can be observed that under tensile forces of 0kN, 100kN, and 200kN, the bending moment causes an increase in contact stress on the compressed side of the sealing surface, while the contact stress on the tensioned side decreases, consistent with the previous discussion.

However, The results in Figure 9 (c), Figure 10 (c) and Figure 11 (c) demonstrate that the contact stress distribution on the sealing surface exhibits a “reversal” phenomenon than that in Figure 9(a), Figure 10 (a), and Figure 11 (a) under the same tensile force, that is, the contact stress decreases on the compressed side while it increases on the tensile side. In Figure 9 (b) and (c), the “reversal” phenomenon occurs between 20MPa and 40MPa when there is no axial tension. Additionally, the results in Figure 10 (a) and (b), and Figure 11 (a) and (b) reveal that the “reversal” phenomenon occurs between 0 and 20 MPa when axial tensile forces is 100 kN and 200 kN, respectively. Based on the simple load analysis results, it can be inferred that when the sealing surface is subjected to bending moments, the sensitivity of the tension side and compression side to internal pressure becomes different. This leads to different contact pressures generated on both sides of the sealing surface for the same value of internal pressure, resulting in “reversal” phenomenon.

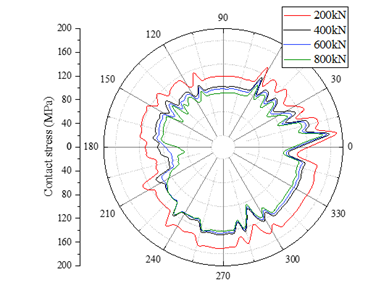
Based on the complex loads analysis results, combined with actual extreme working conditions, internal and external pressure 40MPa. The bending moment based on a dogleg angle 6°/30m. In this section, tension will be treated as the variable, that is, the axial carrying capacity can be obtained by evaluating the contact stress. The circumferential contact stress on the sealing surface for different axial tension under complex loading conditions is shown in Figure 12. The contact stress contour for tension 800 kN is presented in Figure 13.

Figure 12

Figure 12 Contact Pressure Change with Tension

 

Figure 13

Figure 13 Contact Stress Contour for Tension 800 kN

 

In Figure 12, the contact stress on the sealing surface is used as the basis for evaluating the sealing performance Chen et al. (2018). It can be seen that the minimum contact stress on the sealing surface is still greater than the internal pressure when tension is 800 kN, as evident from Figure 13. The results indicate that the joint maintains good sealing performance under this operating condition. In addition, it should be noted that the contact pressure on the sealing surface gradually decreases with increasing tensile load from 200 kN to 400 kN, consistent with the previous findings. Interestingly, when the axial tension increases from 400 kN to 800 kN, the reduction in contact pressure is relatively small. This phenomenon occurs because the contact pressure on the sealing surface is more influenced by internal pressure.

By comparing Figure 13 with Figure 6(c), it can be observed that the difference in contact pressure between the tensile and compressive sides is less pronounced in Figure 13 compared to Figure 6 (c). Combining the result with Figure 12, it can be inferred that when the tension load and internal pressure are relatively low, the bending moment has a significant influence on the distribution of contact pressure. However, when the tension load and internal pressure are relatively high, the effect of the bending moment on the contact pressure distribution becomes less significant.

In summary, under complex loading conditions, the contact pressure distribution on the sealing surface of the joint exhibits a combined effect of multiple factors. Additionally, the distribution of contact stresses on the sealing surface is significantly influenced by internal pressure.

 

4. Conclusions

In this study, the effect of internal pressure, external pressure, axial tension and bending moment on the contact pressure of sealing surface of joints was investigated by the finite element method. Furthermore, the combined effects of these four types of loads on the contact pressure were analyzed. The following conclusions were observed and summarized:

1)     The contact pressure on the sealing surface varies along the axial direction and is not uniformly distributed. This is due to the fact that the joint is not a standard thick-walled cylindrical structure, and changes in its geometric shape can result in variations in contact pressure near abrupt transitions.

2)     Among various factors, external pressure has a relatively minor effect on the contact stress of sealing surfaces. However, when the values of tensile force and internal pressure are within a specific range, it can alter the distribution pattern of contact stress along the axial direction. This alteration is manifested by a transition from decreasing to increasing contact pressure on the sealing surface in the direction away from the joint.

3)     When the joint is subjected to complex loads, the contact stress on the contact surface exhibits a combined effect of multiple factors, and a “reversal” phenomenon occurs in the circumferential contact stress on the sealing surface. This phenomenon is characterized by a decrease in contact stress on the compressive side of the sealing surface and an increase in contact stress on the tensile side due to the bending moment, which is contrary to the influence pattern of bending moment on contact stress observed under simple loading conditions. As the tension load increases, the required internal and external pressures for the occurrence of the "reversal" phenomenon decrease.

4)     For extreme operating conditions, when internal pressure, external pressure and bending moment is maximum, the axial carrying capacity can be obtained by evaluating the contact stress. It is revealed that the BGT1 joint can still maintain a good sealing state when the axial tension reaches 800 kN.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Chen, F., Di, Q.F., Li, N., Wang, C.S., Wang, W.C., & Wang, M.J. (2015). Determination of Operating Load Limits for Rotary Shouldered Connections with Three-Dimensional Finite Element Analysis. Journal of Petroleum Science and Engineering, 133, 622-632. https://doi.org/10.1016/j.petrol.2015.04.029.

Chen, W., Di, Q.F., Zhang, H., Chen, F., & Wang, W.C. (2018). The Sealing Mechanism of Tubing and Casing Premium Threaded Connections Under Complex Loads. Journal of Petroleum Science and Engineering. 171, 724-730. https://doi.org/10.1016/j.petrol.2018.07.079.

Cui, F., Li, W.J., Wang, G.Z., Gu, Z.L., & Wang, Z.S. (2015). Design and Study of Gas-Tight Premium Threads for Tubing and Casing. Journal of Petroleum Science and Engineering, 133, 208-217. https://doi.org/10.1016/j.petrol.2015.06.007.

Dou, Y.H., Cao, Y.P., Zhang, F.X., & Yang, X.T. (2012). Analysis of Influence to the Connect and Seal Ability of Tubing Connection of Inner Pressures, 2nd International Conference on Frontiers of Manufacturing Science and Measuring Technology (ICFMM 2012). Xian, PEOPLES R CHINA, 790. https://doi.org/10.4028/www.scientific.net/AMR.503-504.790.

Galle, T., De Waele, W., & De Baets, P. (2013). Effect of Make-Up on the Structural Performance of Standard Buttress Connections Subjected to Tensile Loading, ASME Pressure Vessels and Piping Conference (PVP-2013). Paris, FRANCE. https://doi.org/10.1115/PVP2013-97282.

Hamilton, K., Wagg, B., & Roth, T. (2009). Using Ultrasonic Techniques to Accurately Examine Seal-Surface-Contact Stress in Premium Connections. Spe Drilling & Completion, 24, 696-704. https://doi.org/10.2118/110675-PA.

Li, Q., Ji, A.M., Liu, W.B., & Fan, X.Y. (2016). Finite Element Analysis on the Sealing Performance of the Casing Premium Thread Connection, International Conference on Mechanics and Materials Science (MMS). Guangzhou, PEOPLES R CHINA, 1172-1178. https://doi.org/10.1142/9789813228177_0150.

Nagata, S., Fujita, S., Sawa, T., & Asme (2020). Fem Stress Analysis and Leakage Behavior of Pipe-Socket Threaded Joints Subjected to Bending Moment and Internal Pressure, ASME Pressure Vessels and Piping Conference (PVP). Electr Network. https://doi.org/10.1115/PVP2020-21221.

Wang, K., Dou, Y.-H., Yu, Y., & Cao, Y.-P. (2015). Application of Three Dimensional Finite Element Method in Evaluation of Seal Characteristic of Premium Connection. International Conference on Mechanics and Mechatronics (ICMM). Changsha, PEOPLES R CHINA, 500-506. https://doi.org/10.1142/9789814699143_0063.

Xu, H., Shi, T., & Zhang, Z. (2014). Theoretical Analysis on Makeup Torque in Tubing and Casing Premium Threaded Connections. Journal of Southwest Petroleum University (Science & Technology Edition), 36, 160-168. (in Chinese). https://doi.org/10.1155/2014/287076.

Yang, B., Xu, H., Xiang, S., Zhang, Z., Su, K., & Yang, Y. (2023). Effects of Make-Up Torque on the Sealability of Sphere-Type Premium Connection for Tubing and Casing Strings. Processes. 11, https://doi.org/10.3390/pr11010256.

Yao, Q. (2019). Analysis of Sealing Performance of BGT1 Oil Pipe. SouthWest Petroleum University. (in Chinese).

Yu, H., Wang, H., & Lian, Z. (2022). An Assessment of Seal Ability of Tubing Threaded Connections: A Hybrid Empirical-Numerical Method. Journal of Energy Resources Technology, 145. https://doi.org/10.1115/1.4056332.

Yu, Y., Dou, Y.H., Zhang, F.X., & Yang, X.T. (2012). Analysis of Premium Connection of Connecting and Sealing Ability Loaded by Axial tensile Loads, 2nd International Conference on Applied Mechanics, Materials and Manufacturing (ICAMMM 2012). Changsha, PEOPLES R CHINA. https://doi.org/10.4028/www.scientific.net/AMM.268-270.737.

Zhang, F. X., Ji, B.Y., Yang, X.T., Han, Y., & Chang, Z.L. (2012). Finite Element Numerical Simulation of Tubing Premium Connection. 2nd International Conference on Advanced Design and Manufacturing Engineering (ADME 2012). Taiyuan, PEOPLES R CHINA. https://doi.org/10.4028/www.scientific.net/AMM.217-219.1622.