Graphs with the burning numbers Equal Three

 

Wen Li ¹

 

¹ School of Mathematics and Statistics, Qinghai Minzu University, Xining, Qinghai 810008, China

 

1.    INTRODUCTION

Recently, a new graph process, defined as graph burning, which is motivated by contagion processes of graphs such as graph searching paradigms (Firefighter Bonato and Nowakowski (2011)) and graph bootstrap percolation Balogh et al. (2012) is proposed by Bonato et al. in Bonato et al. (2014). The purpose of graph burning is to burn all the vertices as quickly as possible. All the graphs considered in this paper are simple, undirected, and finite.

Let  be a graph. Then the graph burning process of  is a discrete time which defined as follows.

Step 1: At time . All the vertices in this time are unburned.

Step 2: At time. One can choose a new unburned vertex  (if such a vertex is available) to burning. And the chosen vertex  is called a source of fire.

If a vertex  is burned, then it must keep burning state until the burning process is finished.

Step 3: At time . All the unburned neighbors of vertex  are burned.

Step 4: If all the vertices of  are burned, then the process ends; Otherwise, turn to Step 2.

The vertex which burned in the time  is denoted by . If a graph  is burned in times, then a burning sequence of  is construct by the sources of fire in each time, denoted by . The burning number  of a graph , is the length of a shortest burning sequence of . Furthermore, the shortest burning sequence of is defined as optimal burning sequence.

It follows from the definition of  that the burning number  of a graph also is the minimum size of the sources of fire after the whole burning process finished. It is clear that the burning number of the star graph is and the complete graph is .

Figure 1 indicates the burning number of  is and is one of its optimal burning sequences.

Figure 1

                                                                     

Figure 1 Burning the path  (the black vertices represent the sources of fire)

 

As proven in Bonato et al. (2015), determining the burning number of a graph  is NP-complete, even for some special graphs such as planar, disconnected, or bipartite graphs. So, it is interesting to study the sharp bounds of the burning number for any connected graphs and characterise the extremal graph. For a general non-trivial connected graph , its burning number , and in Bonato and Nowakowski (2011), the authors showed that  if and only if the maximum degree of  is or . In this paper, we consider some sufficient condition on maximum degree of a graph to have . First, we list some useful notations and known results.

Suppose is a positive integer and is a vertex of , then the set  is the  closed neighbourhood of a vertex .

Proposition 1.1.[1] If a vertex sequence  in graph  such that , then .

Proposition 1.2.[1] For a graph , if  is a spanning subtree of  then .

Proposition 1.3. [1] Let be an isometric subtree of a graph . Then .

Proposition 1.4. [1] If  is a subtree of tree , then .

Proposition 1.5. [1] Let  and  are path and cycle with order , respectively. Then .

Proposition 1.6. [1] Let  be a graph with diameter  and radius . Then ⌈.

Let  be a positive integer and  denote the path with order . A spider graph  is obtained by connecting a disjoint union of paths , with , to a vertex . The maximum degree of the spider graph  is the degree of vertex  that is equal to . Each subgraph  that has same length  is called an arm of .

Proposition 1.7. [1] Let  be a spider graph with maximum degree  and same length  of arms. If , then .

Proposition 1.8. [1] Let  be a graph with order at least 2. Then  if and only if the maximum degree of  is or .

 

2.   Graphs  with

In this section, we characterise graphs with burning number . First, we consider a sufficient condition on the maximum degree of graphs with burning number .

Theorem 2.1. Let  be a tree with order  and maximum degree . If , then .

Proof. Let  be a tree with order  and maximum degree . We first consider the case for . Suppose the vertex  in  with , then there exist five vertices are not adjacent to  in , named ,,,, respectively, and let . Since  is connected, then we have . Now we distinguish five cases to complete the proof:

Case 1. .

This means that  and . Let  and , for . It is clear that .

Case 2. .

Without loss generality, suppose , this means that . Let , and  for . Then .

Case 3. .

Suppose , this means that ,(). Let ,  and , then .

Case 4. .

Suppose , this means that ,(). Consider , the structure of induced subtree  are only six cases, see Figure 2. (a)(b)(c)(d)(e)(f). No matter what case, we always can select ,  such that .

 

 

 

 

 

Figure 2

                                                                    

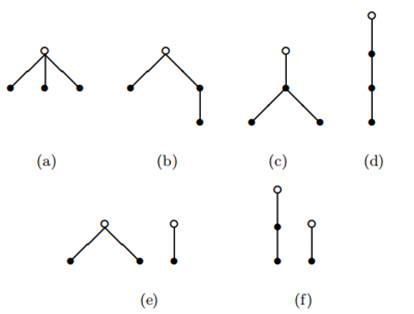
Figure 2 The Structure of Induced Subtree T[S] (The Black Vertices Are V3, V4, V5 and White Vertices Are V1, V2)

 

Case 5. .

Suppose  and ,(). Since  is connected, there is at least one vertex of  adjacent to , suppose  is adjacent to . Now we let  such that , then by similar analysis as (e)(f) of case 4, we can select,  such that .

As for the other cases , we always similar as case  to show that there exits  such that . So by Proposition 1.1, we have . Again, by Proposition 1.8, we know , so we get .

Theorem 2.2. Let  be a connected graph with order  and the maximum degree . If , then .

Proof. By Proposition 1.8, we have . Let  be a spanning tree of graph  satisfies , by Theorem 2.1 and Proposition 1.2, we directly get . So, we have .

In fact, the condition on the maximum degree in Theorem 2.1 is the best possible. We can show that the condition cannot be relaxed to . First, we introduce a spider graph  which is illustrated in Figure 3.

Figure 3

                                                                  

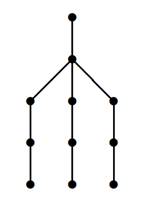
Figure 3 Spider graph

 

Note that  is a subtree of  and  is a subtree of , by Proposition 1.7, we get . Again, by Proposition 1.4, we directly get . Based on this, the following result is clear.

Theorem 2.3. Let  is a tree with order  and maximum degree . If  has an induced subgraph , then .

Next, we consider the necessary condition on maximum degree and bound the number of edges for , respectively.

Theorem 2.4. If the burning number of a connected graph  with order  is , then .

Proof. It is clear that . Further, consider , we suppose the degree of the first and the second fire source are both , then we have . This means we get  . This completes the proof.

Remark 1. The upper bound of Theorem 2.4 meets the comet graph  and the lower bound meets the graph  with order  and  is the square,  obtained from  stars  and  by identifying one 1-degree vertex of  stars  together first to get tree  and then connecting one 1-degree vertex of  and one 1-degree vertex of the last star with .

Theorem 2.5. If the burning number of graphs  with order  is , then .

Proof. If  is connected, then . If  is not connected, consider  and let  has less edges as possible, then  is a forest with three components. So . On the other hand, consider the fact that  if and only if the maximum degree of  is  or . If , the maximum degree of  is . This means we can by removing at least 2 edges from each vertex of complete graph  to estimate the number of edges in . Thus, we are removing a cycle  from  to let . This implies .

Remark 2. The upper bound in Theorem 2.5 meets the comet graph  and the lower bound meets the graph .

 

3.    CONCLUSION

In this paper, we determine the degree condition of a graph  when , and then discuss the bound of the maximum degree and the number of edges in graph  when . However, the sufficient-necessary maximum degree conditions for  are not known, which need further study in future.

 

CONFLICT OF INTERESTS

None. 

 

 

 

ACKNOWLEDGMENTS

The authors would like to thank anonymous reviewers for their valuable comments and suggests to improve the quality of the article. The author was supported by the Science Found of Qinghai Minzu University 2020XJGH14.

 

REFERENCES

Alon, N., Prałat, P., and Wormald, N. (2009). Cleaning Regular Graphs with Brushes. SIAM Journal on Discrete Mathematics, 23(1), 233-250. https://doi.org/10.1137/070703053.

Balogh, J., Bollobás, B., and Morris, R. (2012). Graph Bootstrap Percolation. Random Structures and Algorithms, 41(4), 413-440. https://doi.org/10.1002/rsa.20458.

Barghi, A., and Winkler, P. (2015). Firefighting On a Random Geometric Graph. Random Structures and Algorithms, 46(3), 466-477. https://doi.org/10.1002/rsa.20511.

Bessy, S., Bonato, A., Janssen, J., Rautenbach, D., and Roshanbin, E. (2017). S0166218X17304353. Bounds on the Burning Number. Discrete Applied Mathematics, 232, 73-87. https://doi.org/10.1016/j.dam.2017.07.016.

Bonato, A., Janssen, J., and Roshanbin, E. (2014). Burning a Graph as a Model of Social Contagion. Lecture Notes in Computer Science, 8882, 13-22. https://doi.org/10.1007/978-3-319-13123-8_2.

Bonato, A., Janssen, J., and Roshanbin, E. (2016). How To Burn a Graph. Internet Mathematics, 12(1-2), 85-100. https://doi.org/10.1080/15427951.2015.1103339.

Bonato, A., Janssen, J., and Roshanbin, E. (2015). Burning a Graph is Hard. https://doi.org/10.48550/arXiv.1511.06774

Bonato, A., and Nowakowski, R. J. (2011). The Game of Cops and Robbers on Graphs. American Mathematical Society. https://doi.org/10.1090/stml/061.

Finbow, S., King, A., Macgillivray, G., and Rizzi, R. (2007). The Firefifighter Problem For Graphs of Maximum Degree Three. Discrete Mathematics, 307, 2049-2105. https://doi.org/10.1016/j.disc.2005.12.053.

Finbow, S., and Macgillivray, G. (2019). The Firefighter Problem: A Survey of Results, Directions And Questions. Australasian Journal of Combinatorics, 43, 57-77.

Liu, H., Zhang, R., and Hu, X. (2019). Burning Number of Theta Graphs. Applied Mathematics and Computation, 361, 246-257. https://doi.org/10.1016/j.amc.2019.05.031.

Mitsche, D., Prałat, P., and Roshanbin, E. (2018). Burning Number of Graph Products. Theoretical Computer Science, 746, 124-135. https://doi.org/10.1016/j.tcs.2018.06.036.

Mitsche, D., Prałat, P., and Roshanbin, E. (2017). Burning Graphs-A Probabilistic Perspective, Arxiv :1505.03052. Graphs and Combinatorics, 33(2), 449-471. https://doi.org/10.1007/s00373-017-1768-5.

Roshanbin, E. (2016). Burning A Graph as a Model of Social Contagion [Phd Thesis]. Dalhousie University.

Sim, K. A., Tan, T. S., and Wong, K. B. (2018). On the Burning Number of Generalized Petersen Graphs. Bulletin of the Malaysian Mathematical Sciences Society, 41(3), 1657-1670. https://doi.org/10.1007/s40840-017-0585-6.