PRECISION OF MATHEMATICAL VERBS IN GRADE 12 LEBANESE NATIONAL EXAMS

 

Sanaa Shehayeb ¹

 

¹ Associative Professor, Faculty of Education, Lebanese University, Beirut, Lebanon

 

1. INTRODUCTION

Assessments can be implemented on a large scale or in a classroom. Each type of assessment serves various functions and pursue different objectives.  Large-scale assessments are usually used to provide information, program evaluation, system monitoring, and student placement. Their purpose is mainly graduation or grade promotion, and they frequently depend on student test scores. On the other hand, the purpose of classroom assessments is formative evaluation. They are a variety of teacher-selected assessments directly related to what and how the students have been learning Suurtamm et al. (2016). Large-scale assessments developed through history of mathematics education from problems having one correct solution and one way to solve a problem to a more developed vision of such assessments.  Assessment tasks according to Swan and Burkhardt (2012) should offer a fair representation of the curriculum in which procedures and practices should be taken into consideration in parallel with the content. These tasks should have numerous entry points to students with a variety of abilities and performance levels. They should offer opportunity to show off reasoning processes and be rewarded for them, even if the end output is deficient.

Mathematical language plays a crucial role in students’ learning. Getting students acquainted with the terminology can predict their mathematical performance van der Walt (2009).  The simple and concise mathematical language may be easily integrated into instruction and assessment yielding better student-teacher communication Hughes et al. (2016). Students’ understanding of mathematical concepts is directly related to teacher’s assessment. Referring to the dimension or level of knowledge can be measured if assessments “Attend to precision” as stipulated by the Common Core Standards for Mathematics Akkus (2016) . The lowest cognitive level of educational taxonomies of knowledge is often assigned to the simple reciting of explicit verbal items. It is necessary for the students to demonstrate their possession of a warrant for that knowledge, often a proof in mathematics, in order to show that verbal statements are a portion of warranted personal knowledge as opposed to personal belief or acquaintance with others' knowledge. The highest cognitive level in Bloom's taxonomy, the level of evaluation, generally corresponds to the higher-level ability of producing a warrant for an item of knowledge and explaining why it is a good warrant Ernest (1999). The language of the tests hinders students’ understanding of the questions and thus provides unfair assessment to their understanding and learning Jaber (2019). Vlaardingerbroek et al. (2007) indicates that a recurring issue in Lebanese national exams was that students don’t know exactly what was expected of them in order to receive full credit, particularly when 'justification' was necessary.

 

1.1.    Theoretical Framework

 The interpretation of results of large-scale assessments is often a statistical model, which is a characterization or summary of patterns in the data that one would expect to find given varied degrees of students’ ability. In the context of classroom evaluation, the teacher's interpretation is frequently less formal and is based on an intuitive or qualitative model rather than a rigorous statistical model. In the classroom model, the data acquired, as seen through the lens of the underlying assumptions about how students learn in the area Suurtamm et al. (2016).

The most significant shift in the Revised Bloom Taxonomy is the transition from one to two dimensions. There are two distinct dimensions: the knowledge dimension (noun aspect) and the cognitive process dimension (verb aspect). The intersection of the knowledge and cognitive process categories forms 24 unique cells, as seen in Figure 1. On the other hand, the knowledge dimension is divided into four levels: factual, conceptual, procedural, and metacognitive. The cognitive process dimension across the top of the grid is divided into six levels: remembering, understanding, applying, analyzing, evaluating, and creating Fardin and Radmehr  (2013). Factual knowledge could be interpreted to signify a topic on which the community of math educators is in agreement. The main focus of procedural knowledge is procedure, which is a collection of steps and approved methods for performing mathematics. Conceptual knowledge is the understanding of concepts (such as generalizations, laws of nature, or theorems). Knowing broad techniques for completing various tasks, the circumstances in which they might be employed, and the degree to which they are used are all examples of meta-cognitive knowledge Rizvi (2007).

Figure 1

                                                                       

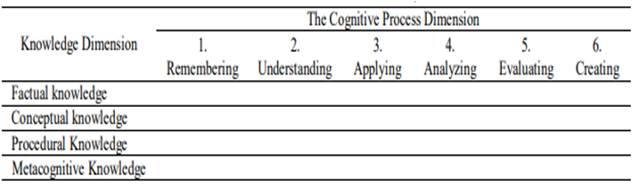
Figure 1 The Two Dimensional- Bloom Taxonomy

 

Porter (2002) developed a rubric for classification of the cognitive dimensions of tasks using five descriptors of categories: (a) memorize; (b) perform procedures; (c) communicate understanding; (d) solve non routine problems; and (e) conjecture/ generalize/prove. The definition for each category is presented in Figure 2.

The framework guiding this study is a link between Bloom taxonomy cognitive and knowledge dimensions and the Porter (2002) rubric.

Figure 2

                                                                      

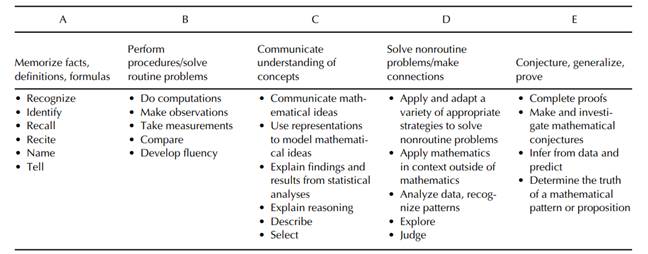
Figure 2 Porter’s Rubric of Language Associated with Performance Goals

 

1.2. Literature Review

Cerdeira et al. (2018) claimed that classroom assessments throughout secondary education are stronger predictors of success in higher education than national test results, both classroom grades and national exam scores are publicly disclosed, so internal grades given by teachers are likely to take into account students' expected performance on those exams; additionally, the incentives to work hard faced by students throughout secondary education are determined by the existence of those national exams. Güler (2021) studied the written test questions implemented by grade 8 mathematics teachers in terms of PISA competency levels. The study's findings revealed that none of the questions asked by teachers until the eighth grade were beyond Level 3. In other words, there were no questions in the last three levels to assess high-level cognitive ability. This raises the issue to track the exam items in terms of cognitive level. On the other hand, Abedi and Lord (2001) investigated the role of language in student test performance on mathematics word problems. Students were given previously available items from the National Assessment of Educational Progress mathematics testing. Items have been updated to lessen their linguistic complexity. During interviews, students generally preferred the updated items to their original equivalents. Paper-and-pencil examinations with original and updated items were given to 1,174 eighth grade students. English language learners (ELLs) performed worse on the arithmetic test than native English speakers. Significant variations in arithmetic performance were seen when test items were linguistically adjusted; scores on the linguistically modified version were marginally higher. This study's findings clearly demonstrate the influence of students' linguistic backgrounds on their performance in mathematics. Shehayeb (2017) performed a cross tabulation of the items in the Lebanese national exams and the TIMSS Advanced cognitive domains. The results revealed a low Porter alignment index equal to 0.34 which raises the alarm to analyze Lebanese mathematics national exam in terms of language and cognitive dimensions.

 

1.3. Purpose

The purpose of this research is to classify the verbs used in official mathematics exams in Lebanon in reference to Bloom cognitive and knowledge dimensions as well as Porter (2002) rubric Figure 1and Figure 2

Research Questions

The research is guided by the following questions:

How can the math assessment verbs in the Lebanese official exams be classified in reference to Porter rubric and Bloom’s knowledge dimensions?

What is frequency of questions at the metacognitive Bloom dimension as compared to other dimensions?

 

2. METHODOLOGY

Grade 12 students in Lebanese schools seeking to major in sciences join the Life Science section or the General Sciences section, whereas those planning to major in social sciences join other sections. Subjects outside of the concentration are given less weight in grading and are less hard on the national test, whereas topics inside the concentration are more challenging and contribute considerably to the final grade Naccache (2012).  Mathematics has a great emphasis in the General Sciences section in the Lebanese national examinations with a weight of 160 out of 570.

This study follows the explorative design. The free- response questions from the Lebanese national mathematics exam for the General Sciences section 2022 were analyzed in terms of Bloom’s cognitive and knowledge dimension as well as Porter’s rubric.

 

3. RESULTS AND DISCUSIONS

The General Science mathematics 2022 exam consists of a multiple-choice question of 4 parts and 4 free response problems related to: probability, complex numbers, transformations, and functions. Each item in every problem is analyzed. The expected outcome is specified, the Porter classification is allotted, and the Bloom cognitive and knowledge dimensions are assigned after consultation with experts in the field for validity and reliability purposes.

Answering research question 1 is displayed in Table 1, and Table 2 taken as a sample in the article and Table 3 and Table 4 in the appendix. Table 1 shows the analysis of the items in the probability problem in the exam. The table presents the items in the problem, the expected outcome from the question, the Porter language associated with the performance goal and the Revised Bloom Taxonomy dimensions. It is worth noting that the classification of items was revised by two experts in mathematics education in order to assure validity. Analyzing the results, it is noted that most of the items are classified as perform procedures/ solve routine problems. All except one is considered on the Applying cognitive level and procedural or conceptual knowledge dimension except for the last item which is considered metacognitive. The same last item is classified as “communicate understanding of concepts” according to Porter. It is also worth noting that the verb “Calculate” was used to deliver expected outcomes at different levels while it is considered in the Applying level according to Bloom Setyaningsih and Listiowarni (2021).

Table 1

Table 1 Analysis of the Problem Related to Probability
Two drawers D1 and D2 contain red and blue crayons. D1 contains 3 red and 2 blue crayons. D2 contains 2 red and 3 blue crayons. One drawer out of the two drawers is chosen at random: If drawer D1 is chosen, then 3 crayons are selected randomly and simultaneously from D1. If drawer D2 is chosen, then 2 crayons are selected randomly and successively without replacement from D2. Consider the following events: A: “The chosen drawer is D1” B: “The selected crayons have the same color”
Item	Expected outcome	Porter’s Classification	Bloom’s cognitive level and knowledge dimension
1) a) Calculate the probabilities  and .	Calculate: write the formula of conditional probability and perform calculation.	Perform procedures/Solve routine problems	Apply- procedural
b) Show that   then calculate .	Validate that the solution is correct by writing the formula and performing the calculation	Perform procedures/Solve routine problems	Apply - Conceptual
2) Knowing that the selected crayons have different colors, calculate the probability that they are selected from drawer D2.	Use the formula of conditional probability to execute the calculation.	Perform procedures/Solve routine problems	Apply - Conceptual
3) Calculate the probability of selecting at least 2 red crayons.	Consider all possibilities and the two drawers	Communicate understanding of concepts	Analyze- Metacognitive

 

Table 2 shows the analysis of the problem related to complex numbers. Four out of the six items are classified as “metacognitive” in Bloom’s knowledge dimension. However, two of them are classified as “Evaluate” in Bloom’s cognitive levels and one of them as Porter “solve non-routine problems”. The verbs used are “write, determine, verify and show” signifying different Porter and Bloom’s levels. Again here, it is noted that the same action verbs are used at different levels. Similar analysis was performed for the questions presented in Table 3 and Table 4 in the Appendix.

Answering research question 2, it is noted that most questions in the exam are classified as “perform procedures/ Solve routine problems” while 4 only out of 32 were non-routine items and none of them is making conjectures and generalizations. Ten items out of 32 are at the metacognitive level which shows that the questions at the higher thinking levels constitute around 30% of the exam. The items classified as Bloom “Evaluate” cognitive level are 9 out of 32 constituting less than 30% of the exam free response items.

Table 2

Table 2 Analysis of the Problem Related to Complex Numbers
The complex plane is referred to a direct orthonormal system Consider the points A, B, M and M′ with affixes , ,  and  such that     with z  i.
Item	Required outcome	Porter’s Classification	Bloom’s cognitive level and knowledge dimension
1) Write z′ in exponential form in the case where z =  + i.	Write z' in algebraic form and then in exponential form	Perform procedures/Solve routine problems	Apply- Procedural
2)  Determine the affix of point M in the case where the point M′ is the midpoint of segment [AB].	Calculate z given M(z’) is the midpoint of [AB]	Perform procedures/Solve routine problems	Apply- Conceptual
3) a) Verify that (z' + 2i) (z – i) = 1 for all z  i.	Confirm that solutions are accurate and appropriate	Perform procedures/Solve routine problems	Apply- Metacognitive
b) Deduce that  and that  where k is an integer.	Use the result of part 3a and translate the complex number statement vectorially.	Communicate understanding of concepts	Evaluate- Metacognitive
c) When M varies on the circle (C) with center A and radius 2, show that M' varies on a circle whose center and radius are to be determined.	Interpret the findings geometrically	Communicate understanding of concepts	Understand - Metacognitive
d) Show that if M varies on the semi line [Ay) deprived of point A, then O is a point on the segment [MM'].	Interpret a geometric problem vectorially and verify the solution	Solve non-routine problems/ Make connections	Evaluate-Metacognitive

 

 

4. CONCLUSION AND RECOMMENDATIONS

This study targeted the Lebanese national mathematics exams- General Sciences section- where emphasis is on mathematics. The results showed an ambiguity in the use of action verbs which can be classified differently in Porter and Bloom levels. It also classified the free response items in the exam for Porter and Bloom cognitive and knowledge dimensions which showed that the exam items visited various levels except for Porter highest level pointing conjectures and generalizations. Porter high stake level was not targeted in the exam which conforms with previous research results Shehayeb (2017). This research comes with a limitation regarding the sample used. More samples of national exams with different mathematics emphasis should be targeted.  This research calls for more emphasis on higher Bloom and Porter levels items. It recommends that future research informs national test administrators and experts of the correct usage of action verbs in mathematic exams.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Abedi, J., and Lord, C. (2001). The Language Factor in Mathematics Tests. Applied Measurement in Education, 14(3), 219-234. https://doi.org/10.1207/S15324818AME1403_2.

Akkus, M. (2016). The Common Core State Standards for Mathematics. International Journal of Research in Education and Science, 2(1), 49-54.

Cerdeira, J. M., Nunes, L. C., Reis, A. B., and Seabra, C. (2018). Predictors of Student Success in Higher Education : Secondary School Internal Scores Versus National Exams. Higher Education Quarterly, 72(4), 304-313. https://doi.org/10.1111/hequ.12158.

Ernest, P. (1999). Forms of Knowledge in Mathematics and Mathematics Education : Philosophical and Rhetorical Perspectives. Forms of Mathematical Knowledge, 67-83. https://doi.org/10.1007/978-94-017-1584-3_4.

Fardin, D., and Radmehr, F. (2013). A Study on K5 Students' Mathematical Problem Solving Based on Revised Bloom Taxonomy and Psychological Factors Contribute to It. European Journal of Child Development, Education and Psychopathology, 1(3), 97-123. https://doi.org/10.30552/ejpad.v1i3.8.

Güler, M. (2021). An Investigation of the Questions Mathematics Teachers Use on Exams. Journal of Pedagogical Research, 5(1), 141-153. https://doi.org/10.33902/JPR.2021167371.

Hughes, E. M., Powell, S. R., and Stevens, E. A. (2016). Supporting Clear and Concise Mathematics Language : Instead of that, Say this. Teaching Exceptional Children, 49(1), 7-17. https://doi.org/10.1177/0040059916654901.

Jaber, D. G. (2019). Validity, Accountability and Fairness of Official Exams in Lebanon : Reflections of Grades 9 and 12 Public School Students (Doctoral Dissertation, Notre Dame University-Louaize).

Naccache, H. S. (2012). Factors Related to Student Performance in Statistics Courses in Lebanon. The University of Southern Mississippi.

Patterson, B. F., Packman, S., and Kobrin, J. L. (2011). Advanced Placement Exam-Taking and Performance : Relationships With First-Year Subject Area College Grades. Research Reports No. 2011-4. College Board.

Rizvi, F. (2007). A Synthesis of Taxonomies/Frameworks Used to Analyse Mathematics Curricula in Pakistan. Proceedings of the British Society for Research into Learning Mathematics, 27(3), 90-95.

Setyaningsih, E. R., and Listiowarni, I. (2021). Categorization of Exam Questions Based on Bloom Taxonomy Using Naïve Bayes and Laplace Smoothing. In 3rd East Indonesia Conference on Computer and Information Technology (Eiconcit), 2021. IEEE Publications, 330-333. https://doi.org/10.1109/EIConCIT50028.2021.9431862.

Shehayeb, S. (2017). Alignment of Lebanese National Examinations and TIMSS Advanced Mathematics Study. Journal of Educational Research, 110-128. x

Suurtamm, C., Thompson, D. R., Kim, R. Y., Moreno, L. D., Sayac, N., Schukajlow, S., and Vos, P. (2016). Assessment in Mathematics Education : Large-Scale Assessment and Classroom Assessment. Springer Nature. https://doi.org/10.1007/978-3-319-32394-7.

Swan, M., and Burkhardt, H. (2012). Designing Assessment of Performance in Mathematics Educational Designer, 2(5).

Van den Heuvel-Panhuizen, M., and Becker, J. (2003). Towards a Didactic Model for Assessment Designin Mathematics Education. In A. J. Bishop, M. A. Clements, C. Keitel, J. Kilpatrick and F. K. S. Leung (Eds.), Second International Handbook of Mathematics Education. Kluwer Academic Publishers. 686-716. https://doi.org/10.1007/978-94-010-0273-8_23.

Vlaardingerbroek, B., Jaber, L. Z., Rizk, N. G., and Bayoud, J. M. (2009). The Lebanese Brevet Chemistry and Physics Examinations: An Exploratory Study. International Journal of Science and Mathematics Education, 7(6), 1227-1247. https://doi.org/10.1007/s10763-009-9159-x.

Webb, N. L. (1997). Criteria for Alignment of Expectations and Assessments in Mathematics and Science Education. Research Monograph, 6.

 

APPENDICES

Table 3

Table 3 Analysis of the Problem Related to Transformations
·        In the figure below, ·        ABCD is a direct rectangle. ·        AB = 2 and BC = 1. ·        I is the midpoint of [DC]. ·        (d) is the perpendicular to (BI) at B. ·        J is the point of intersection of (d) and (AD).
Part A Let S be the direct plane similitude with center B that transforms C onto A.
Item	Required outcome	Porter’s Classification	Bloom’s cognitive level and knowledge dimension
1) Calculate the ratio k of S and determine an angle  of S.	choose the correct sides to calculate the ratio and the correct oriented angle	Perform procedures/Solve routine problems	Evaluate- conceptual
2a) Show that the image of the line (CI) by S is the line (AD).	Apply the properties of similitude to find the image of a line.	Perform procedures/Solve routine problems	Evaluate- Conceptual
2b) Determine the image of (BI) by S and verify that S(I) = J.	Use properties of similitude to find the image of a line and then use the intersection property to verify that the image of I is J	Perform procedures/Solve routine problems	Apply- Conceptual
3) Let (C) be the circle with diameter [BI]. a) Determine (C') the image of (C) by S.	Use the property that the diameter of image of a circle by a similitude is the image of the diameter of the original circle	Perform procedures/Solve routine problems	Understand- Conceptual
b) Prove that the image of the line (AI) by S is tangent to (C').	Prove that the line (AI) is tangent to the original circle (C).	Solve non-routine problems/ Make connections	Evaluate- metacognitive
Part B Let R be the rotation with center I and angle – π/2 and h = S ∘R.
Item	Required outcome	Porter’s Classification	Bloom’s cognitive level and knowledge dimension
1)Determine h(I).	Apply the composite transformation to find h(I)	Solve non-routine problems/ Make connections	Evaluate- metacognitive
2) Prove that h is a dilation whose ratio is to be determined.	Find the ratio and center of h	Solve non-routine problems/ Make connections	Evaluate- metacognitive
Part C The plane is referred to the direct orthonormal system (A; u┴→,v┴→ ), with z_B = 2, z_D = i, and z_"J"  = –2i.
Item	Required outcome	Porter’s Classification	Bloom’s cognitive level and knowledge dimension
1)Determine the complex form of h.	Interpret the dilation in algebraic terms	Perform procedures/Solve routine problems	Apply - Procedural
2)Let W the center of h. Determine the affix of W.	Use the property that the center is invariant to calculate its affix	Perform procedures/Solve routine problems	Apply- Procedural

 

  Table 4

Table 4 Analysis of the Problem Related to Functions
Consider the function of defined on  as . Denote by  the representative curve of f in an orthonormal system .
Item	Required outcome	Porter’s Classification	Bloom’s cognitive level and knowledge dimension
1) a) Determine. Deduce an asymptote to .	Use the properties of exponential functions to find the limit and interpret the result graphically	Perform procedures/Solve routine problems	Apply- Procedural
b) Find the coordinates of the point of intersection of (C) and (d).	Perform calculations to find the abscissa and ordinate of the point of intersection	Perform procedures/Solve routine problems	Apply- Procedural
1) Determine  and calculate f (-2.5).	Use the properties of exponential functions to find the limit and perform calculations to calculate the ordinate.	Perform procedures/Solve routine problems	Apply- Procedural
2) Verify that  =  and set up the table of variations of f.	Use the properties of the derivatives of exponential functions and interpret the sign in a table.	Perform procedures/Solve routine problems	Apply- Procedural
3) a) Show that the equation has a unique root  on .	Apply the intermediate value theorem	Communicate understanding of concepts	Analyze- Conceptual
b) Verify that -2.2  -2.1.	Show that the images have opposite signs	Perform procedures/ Solve routine problems	Apply- Procedural
4) a) Prove that the point I (0, 3) is the point of inflection of the curve (C).	Find the second derivative vanishes and show that it changes sign at x=0	Communicate understanding of concepts	Evaluate- Conceptual
b) Determine an equation of (T), the tangent to (C) at I.	Apply the formula to find the equation of the tangent line.	Communicate understanding of concepts	Apply- Procedural
c) The table below is the table of variations of the function g defined as . x                         0                        g(x) 0 Deduce, according to the values of x, the relative positions of (C) and (T).	Discover the relation between the functions g and f then interpret the table of variations to deduce the relative positions of the curve and the tangent.	Solve non-routine problems/ Make connections	Analyze- Metacognitive
5) Draw (d),  and (C).	Represent the function graphically	Perform procedures/Solve routine problems	Apply- Procedural
6) Let k be the function given by k(x) =  . Denote by (C') the representative curve of k in an orthonormal system. a) Determine the domain of definition of k.	Apply the properties of the logarithmic function to find the domain of definition of k	Perform procedures/Solve routine problems	Apply- Procedural
b) Show that k'(α) =  .	Use the property of α from 3b to perform the calculations	Solve non-routine problems/ Make connections	Evaluate- Metacognitive
c) Show that the tangent to (C') at the point with abscissa α intersects the y-axis at the point W.	Perform calculations to find the coordinates of point W.	Perform procedures/Solve routine problems	Apply- Procedural