ON THE LANZHOU INDEX OF GRAPHS
Qinghe Tong
1
,
Chengxu Yang 2
, Wen Li 2
1 School of Mathematics and Statistics,
Qinghai Normal University, Xining, Qinghai 810008, China
2 School of Computer, Qinghai Normal
University, Xining, Qinghai 810008, China
|
|
|
ABSTRACT |
|
|
Let |
|||
|
Received 29 October 2022 Accepted 30 November 2022 Published 10 December 2022 Corresponding Author Chengxu
Yang, cxuyang@aliyun.com DOI10.29121/granthaalayah.v10.i11.2022.4916 Funding: This research
received no specific grant from any funding agency in the public, commercial,
or not-for-profit sectors. Copyright: © 2022 The
Author(s). This work is licensed under a Creative Commons
Attribution 4.0 International License. With the
license CC-BY, authors retain the copyright, allowing anyone to download,
reuse, re-print, modify, distribute, and/or copy their contribution. The work
must be properly attributed to its author.
|
|||
|
Keywords: Lanzhou Index, Silicate Network, Graph
operation |
|||
1. INTRODUCTION
In this paper, we consider simple, connected, and finite graphs. For a vertex 
,
the number of all edge incidents with 
is denoted by 
,
the maximum (minimum) degree of 
is denoted by 
Moreover, we let
and 
，
.
The topological index is very useful in chemistry, its
value is related to the molecular structure-activity of the compound. The first
Zagreb index 
and the second Zagreb
index 
,
introduced by Kazemi in Kazemi
and Behtoei (2017), are defined as
Furtula and Gutman in Furtula
and Gutman (2015) introduced the
forgotten index of ,
which is defined by
After that, Vukičević et al. Vukičević et al. (2018). introduced an index named by Lanzhou index, which is defined as
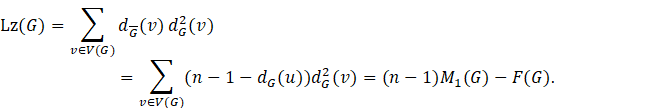
Let 
= 
be the line graph of .
The vertex of corresponds to the edge of .
Two vertices of are adjacent if and only if the corresponding
edge of is adjacent. Then we have 
.
Line graphs are widely used in the field of chemistry. For example, Nadeem
studied 
and 
indices of the line graph of the wheel,
tadpole in paper Nadeem
et al. (2015). Randić found that the connectivity index
of a line graph in some molecular graph is highly correlated with some
physicochemical properties. Gutman further proposed the application of line
graphs in physical chemistry. All this mean that in the field of topology, line
graph is extremely important in the study of chemistry and physics. By
definition of line graph, we have the following observation. From the
definitions, the following observation is immediate.
2.1. Results for line graphs
Observation 1. Let be
a graph, for 
,
and 
,
we have
and 
.
Theorem 2.1. Vukičević et al. (2018). Let be a connected graph of order 
.
Then we have 
.
The inequality is satisfied if and only if is
either complete or empty graph.
Theorem 2.2.
Let be a
connected graph with order 
and 
. Then
With right equality holding if and only if and only if 
is a regular graph
and the lower bound is sharp.
Proof. For the up bound, by
definition of Lanzhou index, we have
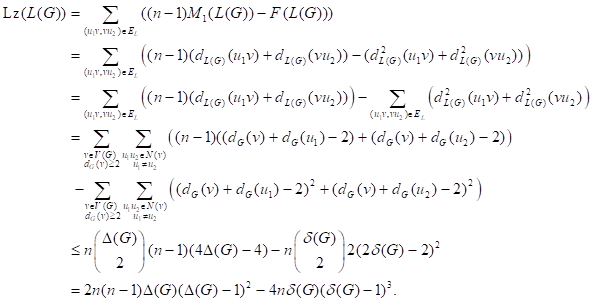
With equality holds if and only if is a regular graph.
In addition, for
the lower bound, from Theorem 2, it follows that .
Let is 
or 
or star graph 
,
it follows that 
is an empty graph or a complement graph, from
theorem 2, we have
.
So, the lower bound is sharp.
2.2. Results for line graph of graphene sheet
Graphene 
is a 2-dimensional layer of pure carbon. Line
graph of graphene
is shown below in Figure 1
Figure 1
|
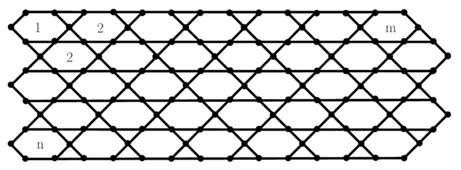
Figure 1 |
Theorem 2.3. Let 
are two integers, 
,
and let be a molecular graph of graphene with rows and 
columns. Then
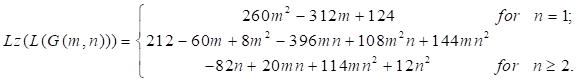
Proof. For 
, we have 
,
,
,
and 
.
Let 
.
From the definition of Lanzhou index, we have that
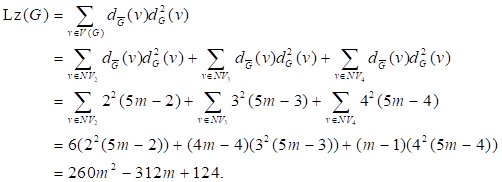
Similarly, for 
,
we have 
，
,
,
and 
.
Let .
Hence
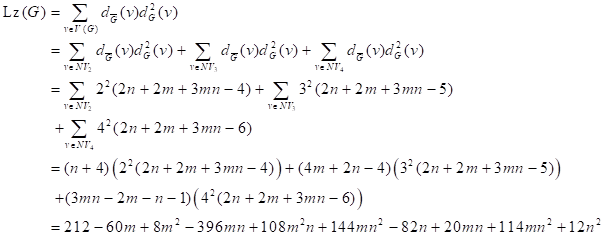
2.3. Results for line graph of DENDRIMER STARS
Nanostar dendrimers are generally synthesized by divergent
or convergent methods. It is a kind of hyperbranched nanostructures. 
and 
are the line graph of three dendrimers and
widely appear in drug structure, see Figure 2, Figure 3, Figure 4.
Figure 2
|
Figure 2 Line Graph of Nanostar Dendrimer |
Figure 3
|
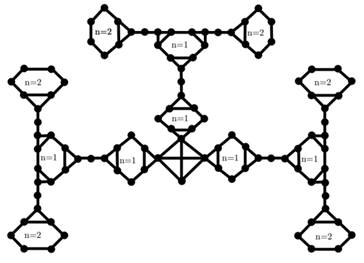
Figure 3 Line Graph of Nanostar Dendrimer |
Figure 4
|
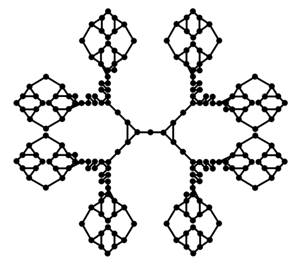
Figure 4 Line Graph of
Nanostar Dendrimer |
Theorem 2.4. Let are two integers. Then the Lanzhou index of
line graphs of three infinite classes ,
and of dendrimer stars are
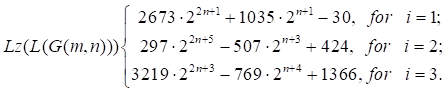
Where 
is the number of steps
of growth of these three families of dendrimer stars.
Proof. For 
,
we have 
,
,
,
and 
.
Let 
.
We have
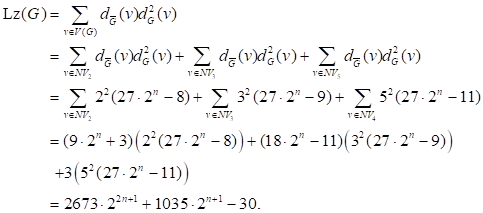
Similarly, for 
,
we have 
,
,
and 
.
Let 
.
Then we have
For 
,
we have 
,
,
, and 
.
Let 
.
By the definition of Lanzhou index, we have
3. Results for CHAIN SILICATE NETWORKS GRAPH
In this section, we consider a family of chain silicate
networks. This network is denoted by 
and is obtained by arranging tetrahedral linearly, see Figure 5.
Figure 5
|
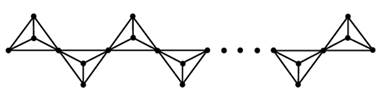
Figure 5 |
We refer the reader to article Kazemi
and Behtoei (2017) for some aspects of
the parameters of silicate networks. Obviously, for any silicate networks 
, 
and 
.
Theorem 3.1. Let be a positive integer,
for an n-long silicate networks ,
we have 
Proof. Obviously, .
Note that is consist of n tetrahedrons which connected
by linear chains. Then we have 
and 
.
Let 
,
we
get
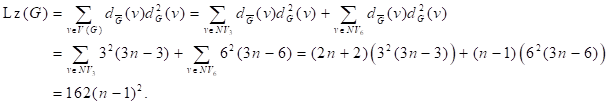
Define the honeycomb network as
. 
is number of layers
from the center to the boundary in 
. We use a honeycomb network to constructe the silicate
network 
by placing silicon
ions on all the vertices of , and dividing the edges and placing oxygenions on the new
vertices, last placing oxygenions at the pendent vertices, where the silicate
network defined as 
.
When 
, the silicate network is as follow.
Figure 6
|
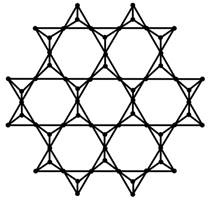
Figure 6 |
Obviously, for the silicate networks , we have
and 
. The set of edges can decompose as three
types:
Type (1): 
Type (2): 
Type (3): 
Clearly, we have 
.
Theorem 3.2. For 
,
the Lanzhou index of hexagons with size 
is
Proof.
For , we have 
, 
and 
. Let 
. By the definition of Lanzhou index, we have that
4. RESULTS FOR SIERPIńSKI GRAPHS
Graphs are widely
used in topology, psychology, and probability Hinz and Schief (1990), Kaimanovich (2001), Klix and Goede (1967).The sierpiński graphs 
was introduced by
Pisanski et al. in Pisanski and Tucker (2001).
Let 
be
the vertex set of 
, , 
. The edge 
is between two vertices 
and 
. If there is an integer 
such that
The Sierpiński
graph 
is shown in Figure 7.
Theorem 4.1. The Lanzhou index of Sierpiński
graph 
(also named the Tower of Hanoi with n disks) (
)
is 
.
Proof. Let 
. Obviously, the degree of vertex 
is either 2 or 3. It
is clear that 
and 
. Then
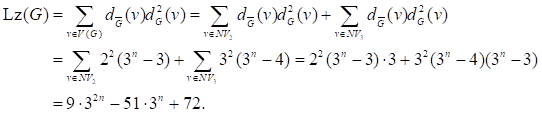
The
Sierpiński gasket graphs are extended versions of the Sierpiński
graph. In 2008, Alberto and Anant introduced Sierpiński gasket graph Teguia and Godbole (2006). The sierpiński gasket 
is obtained by shrinking all bridge edges of . Sierpiński gasket 
is shown in Figure 8.
Figure 7
|
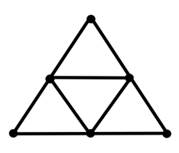
Figure 7 |
Figure 8
|
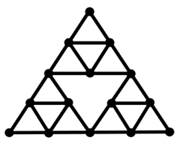
Figure 8 |
Theorem 4.2. The Lanzhou
index of Sierpiński gasket graph 
is
Proof. In Sierpi´nski gasket graph 
,
,
, and the set of edges can decompose as two
types:
Type (1): 
Type (2): 
Clearly, we have 
.
Let 
,
by the definition of Lanzhou index, for 
, we have 
,
. 
. Then we have
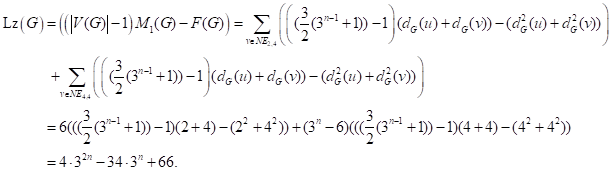
Theorem 4.3.
The Lanzhou index
of Sierpiński gasket graph 
is
Proof, there are 
vertices in . The number of 
degree vertex is 
, and the number of degree vertex is 
. Next, we consider the vertex in the complement graph
of 
. In 
,
the number of 
degree vertex is 
, and there are 
vertices with degree .
Note that 
and 
.
Let 
.
Then we have
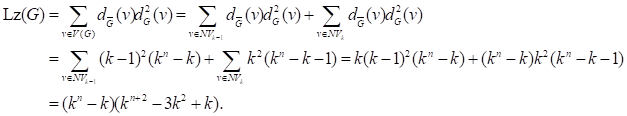
The Sierpiński Gasket Rhombus of level 
is defined by 
, which obtained by identifying the
edges in two copies of along one of their sides and 
Sierpiński Gasket Rhombus 
show in Figure 9.
Figure 9
|
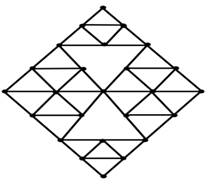
Figure 9 Sierpiński
Gasket Rhombus |
Theorem 4.4.
If is a Sierpiński Gasket Rhombus graph.
Then
.
Proof. Note
that 
,
, 
, 
, 
, and 
. Let 
and 
, clearly, 
.
Therefore, we have
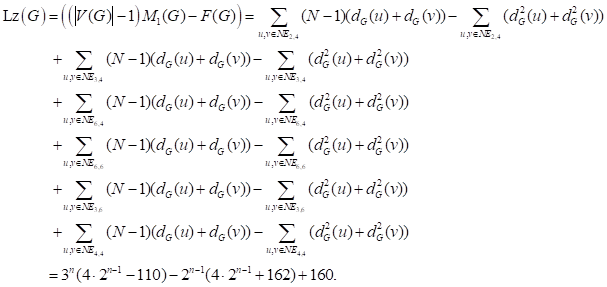
5. LANZHOU INDEX OF CACTUS CHAINS
NETWORKS
The Cactus chain is a simple connected graph. Husimi and Riddell first studied the Cactus graph in Husimi (1950). These graphs are widely used in many fields such as the theory of electrical and communication networks Zmazek and Zerovnik (2005). and in chemistry Zmazek and Zerovnik (2003).
Theorem 5.1. The Lanzhou index of different types of Cactus graphs.
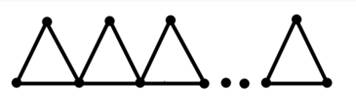
Use 
represent the chain triangular graph (See Figure 9). Then 
.
Use 
represent the
para-chain square cactus graph (See Figure 10). Then 
.
Use 
represent the
para-chain square cactus graph (See Figure 11). Then 
.
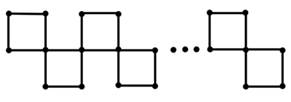
Use 
represent the
Ortho-chain graph (See Figure 12).Then 
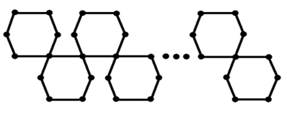
Use 
represent the para-chain hexagonal cactus
graph (See Figure 13). Then 
.
Use 
represent the
Meta-chain hexagonal cactus graph (See Figure 14). Then 
.
Figure 10
|
Figure 10 |
|
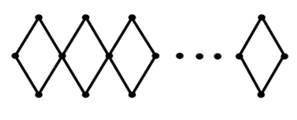
Figure
11 |
Figure 12
|
Figure 12 |
Figure 13
|
Figure 13 |
Figure 14
|
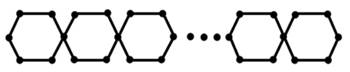
Figure 14 |
Figure 15
|
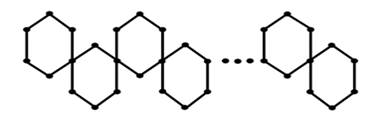
Figure 15 |
Proof.
1) Note
that 
,
,
,
and 
.
Therefore, we have
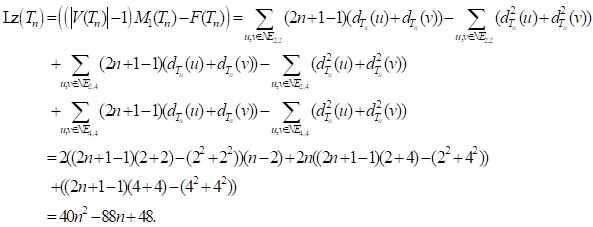
2) Note
that there are four edges with end-vertex of degree 2. Also there are 
edges with end-vertex of degree 2 and 4. So we have 
, 
and 
.Therefore, we have
3) Note
that there are 
edges with end-vertexs
of degree 2, there are 
edges with end-vertexs
of degree 2 and 4, and there are 
edges with end-vertexs
of degree 4. Then we have 
,
,
and .Therefore, we have
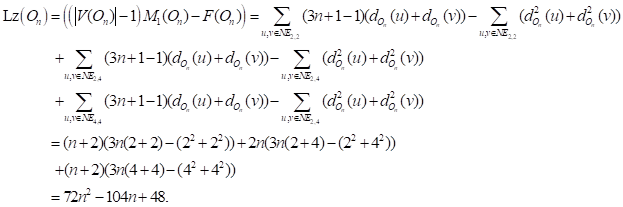
4) There
are 
edges with end-vertex of degree 2, there are 
edges with end-vertex
of degree 2 and 4, and there are 
edges with end-vertex of degree 4. Then we have
, 
,
and .
Therefore, we have
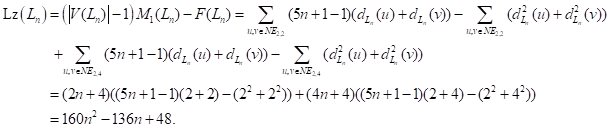
6) Since
,
and 
. Then, we have
6. RESULTS FOR SOME OPERATIONS
For any integer 
, the k-subdivision of is denoted by 
which is constructed by replacing each edge of
with a path of length 
. Then, we have following result about the Lanzhou index of
k-subdivision of graph .
Theorem 6.1. Let 
be a graph with
order 
size 
, .
For every .
We have
.
Proof. There are 
edges with end-vertex
of degree 2 and .
Also, there are 
edges with end-vertex of degree 2 and 2.
Therefore, we have
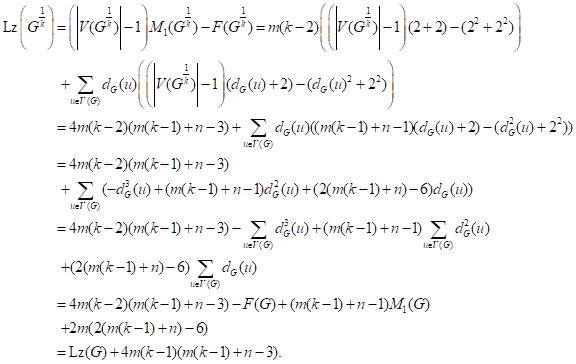
By the proof of Theorem 13, we get Observation as below.
Observation 2. Let 
. Then we have
.
We next describe some common binary operations defined on
graphs. In the following definitions, let 
and 
are two graphs with disjoint vertex sets. The
join 
of and has vertex set 
and edge set
.
By the definition of join operation and the definition of Lanzhou index, we have following observation.
Observation 3. Let and 
are two graphs with
order 
and 
, respectively. Then we have
Theorem 6.2. Let be a graph with order and size 
,
and let H be a graph with order and size 
.
Then we have
.
where 
.
Proof. From Observation 16, we have that
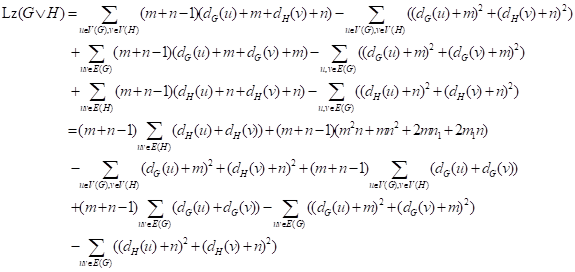
It is obviously, we have that
So, we have following equation.
Equation 1
It is obviously that
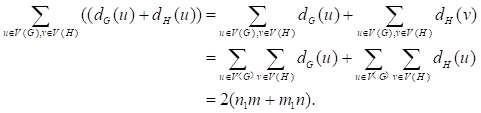
So, we get equation
Equation
2
It is obviously that
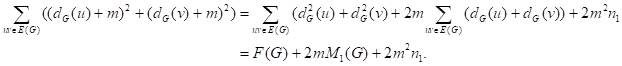
So, we get equation
Equation 3
Similarly, we get equation
Equation 4
By equation Equation 1, Equation 2, Equation 3, and Equation 4, we have
.
Where .
Let be a graph with order .
The Corona of and 
is defined as the graph obtained by taking one
copy of graph and taking n copy of graph ,
then, join ith vertex of to the vertexs in the i th copy of .
Observation 4. Let and be two graphs,
and 
.
Then we have
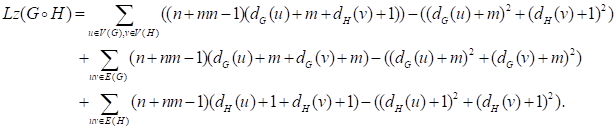
By Observation 18, we have result as below.
Theorem 6.3. Let 
be a graph with order and size ,
and let 
be a graph with order and size .
Then we have Let
.
where
.
Proof. By Observation 18, it follows that
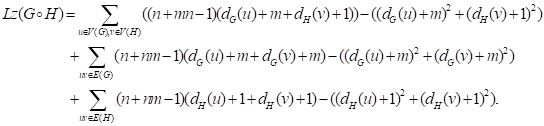
It obviously that
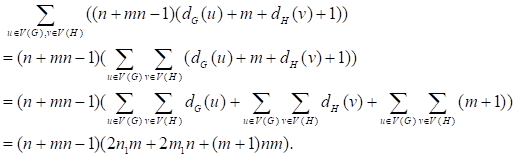
So, we have following equation
Equation 5
Since that
So, it follows that
Equation 6
Since that
So, it follows that
Equation 7
Since that
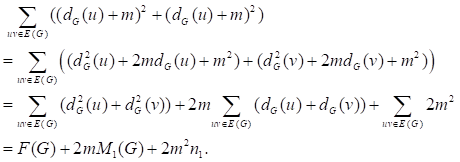
So, it follows that
Equation 8
So, it follows that
Equation 9
Since that
So, it follows that
Equation 10
By Equation 5, Equation 6, Equation 7, Equation 8, Equation 9, and Equation 10, we have that
.
where 
.
CONFLICT OF INTERESTS
None.
ACKNOWLEDGMENTS
The third author was supported by the National Science Foundation of China (Nos. 11601254, 11551001, 11161037, 61763041, 11661068, and 11461054) and the Qinghai Key Laboratory of Internet of Things Project (2017-ZJ-Y21).
REFERENCES
Chartrand, G., Lesniak, L., and Zhang, P. (1996). Graphs and Digraphs. Chapman & Hall.
Furtula, B., and Gutman, I. (2015). A Forgotten Topological Index. Journal of Mathematical Chemistry, 53(4), 1184–1190. https://doi.org/10.1007/s10910-015-0480-z.
Hinz, A. M., and Schief, A. (1990). The Average Distance on the Sierpiński Gasket. Probability Theory and Related Fields, 87(1), 129–138. https://doi.org/10.1007/BF01217750.
Husimi, K. (1950). Note on Mayer’S Theory of Cluster Integrals. Journal of Chemical Physics, 18(5), 682–684. https://doi.org/10.1063/1.1747725.
Kaimanovich, V. A. (2001). Random Walks on Sierpiński Graphs : Hyperbolicity and Stochastic Hom-Ögbenization, Fractals in Graz, 145–183.
Kazemi, R., and Behtoei, A. (2017). The First Zagreb and Forgotten Topological Indices of D-Ary Trees, Hac-Ettepe. Journal of Mathematics and Statistics, 46(4), 603–611.
Klix, F., and Goede, K. R. (1967). Struktur and Komponenten analyse von Problem lö sungsprozersen. Zeitschrift für Psychologie, 174, 167–193.
Manuel, P., and Rajasingh, I. (2009). Topological Properties of Silicate Networks, IEEE.GC.Confe.Exhi, 5, 1–5. https://doi.org/10.1109/IEEEGCC.2009.5734286.
Nadeem, M. F., Zafar, S., and Zahid, Z. (2015). On Certain Topological Indices of the Line Graph of Subdivision Graphs. Applied Mathematics and Computation, 271, 790–794. https://doi.org/10.1016/j.amc.2015.09.061.
Pisanski, T., and Tucker, T. W. (2001). Growth in Repeated Truncations of Maps, Atti Sem. Mat. Fis. Univ. Modena, 49, 167–176.
Teguia, A. M., and Godbole, A. (2006). Sierpiński Gasket Graphs and Some of their Properties, Australasia-n. J. Combin, 35, 181–192. https://doi.org/10.48550/arXiv.math/0509259.
Vukičević, D., Li, Q., Sedlar, J., and Dǒslić, T. (2018). Lanzhou Index, MATCH Commun. Match. Computers and Chemistry, 80, 863–876.
Zmazek, B., and Zerovnik, J. (2003). Computing the Weighted Wiener and Szeged Number on Weighted Cactus Graphs in Linear Time. Croatica Chemica Acta, 76, 137–143.
Zmazek, B., and Zerovnik, J. (2005). Estimating the Trac on Weighted Cactus Networks in Linear Time, Ni-nth International Conference on Information Visualisation, 536–541.
This work is licensed under a: Creative Commons Attribution 4.0 International License
© Granthaalayah 2014-2022. All Rights Reserved.
