SOMBOR INDEX OF LINE AND TOTAL GRAPHS AND PERICONDENSED BENZENOID HYDROCARBONS

 

Yue Li ¹ , Qingcuo Ren ¹,  Jinxia Liang ¹, Chengxu Yang ², Qinghe Tong ¹

 

¹School of Mathematics and Statistics, Qinghai Normal University, Xining, Qinghai 810008, China

² School of Computer, Qinghai Normal University, Xining, Qinghai 810008, China

 

1. INTRODUCTION

In the mathematical and chemical literature, several dozens of vertex-degree-based graph invariants have been introduced and extensively studied in Pal et al. (2019), Todeschini and Consonni (2009).  For a graph , let  ,  and  and  denote the  size, the minimum degree and the maximum degree and the degree of the vertex , respectively. The line graph  is the graph whose vertex set is the edges of, two vertices   and  of   being adjacent if and only if corresponding edges in  are adjacent. The total graph   of a graph is the graph whose vertex set is with two vertices of being adjacent if and only if the corresponding elements of are either adjacent or incident.

Recently,  Gutman (2021) introduced a new index defined as

 

                                               Equation 1

 

called Sombor index.

      The distance Gutman (2021)   between the d-point   and the origin of the coordinate system is the degree-radius (or d-radius) of the edge , denoted by   Based on elementary geometry 

(Using Euclidean metrics), we have

 

                                                                                             

 

In Gutman (2021), Gutman presented a novel approach to the vertex-degree-based topological indices of (molecular) graphs. The upper and lower bounds of Sombor index for general trees and graphs are given, and some basic properties of the Sombor index are established. Cruza et al. (2021) characterized the graphs extremal with respect to the Sombor index over the following sets: (connected) chemical graphs, chemical trees, and hexagonal systems. Das and Gutman Das and Gutman (2022) presented bounds on SO index of trees in terms of order, independence number, and number of pendent vertices, and characterize the extremal cases. The mathematical relations between the Sombor index and some other well-known degree-based descriptors was investigated in Wang et al. (2022).

In 2015, Su and Xu (2015) studied the general sum-connectivity index and co-index of line graph of subdivision graphs. In 2021, Demirci et al. (2021) obtained the explicit expressions for the Omega index of line and total graphs. In Section 2, the Sombor index of   and  are determined, respectively.

Klavˇzar et al. (1997)determined the explicit expressions of Wiener index for
several pericondensed benzenoid hydrocarbons.  We also determine the explicit expressions of
Sombor index for several pericondensed benzenoid hydrocarbons in Section 3.

 

2. RESULTS FOR LINE AND TOTAL GRAPHS

From the definitions, the following observation is immediate.

Observation 1.  Let  be a graph, , and . Then

 

  and  .     

 

Theorem 2.1.   Let  be a connected graph of order n, with maximum degree  and minimum degree . Then

 

                                                             

 

with equality if and only if is a regular graph.

Proof.  From the definition of Sombor index, we have

 

        

 

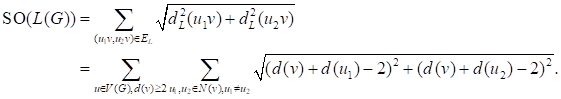
Since , it follows that

 

                                                                                                                                                                              

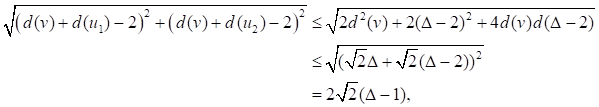
with equality if and only if .

For any vertex , let  denote the set of vertices associated with v. Since and   , it follows that

 

                                                                                   

 

Similarly, to Theorem 2.1, we can give a lower bound of  without its proof.

 

Observation 2.  Let  be a graph,  , . Then  and .

Theorem 2.2.  Let  be a connected graph of order n with m edges such that its maximum and minimum degrees are  and , respectively. Then

 

                              

 

with equality if and only if  is a regular graph.

Proof.  Let

 

 

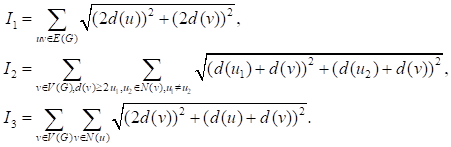
From the definition of Sombor index, we have

            

                                                                                                  

 

Since  , it follows that

 

                                                                                                  

 

For any vertex , since  and

 

, it follows that

 

                                                                                            

                                                                                                                           

 

and hence 

 

                               

 

with equality if and only if  is a regular graph.

 

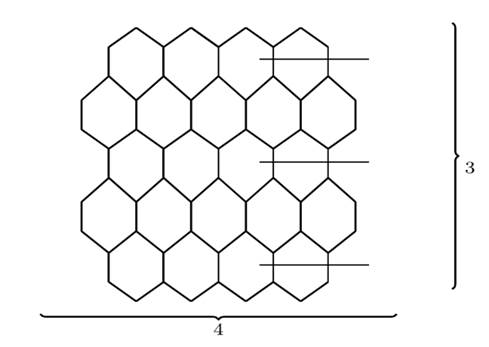
3. RESULTS FOR PERICONDENSED BENZENOID HYDROCARBONS

In this section, we determine the explicit exact values for Sombor index of several pericondensed benzenoid hydrocarbons.

 

3.1. PARALLELOGRAM BENZENOID SYSTEM

For  and , let  be the parallelogram benzenoid system. The definition of  should be clear from the example  shown in Figure 1, Klavˇzar et al. (1997).

Figure 1

                                                        

Figure 1 Parallelogram Benzenoid System

 

Theorem 3.1. Let  be two integers with  and  . Let   be the parallelogram benzenoid system. Then

 

         

 

Proof. For  , we have  . From the definition of Sombor index, we have

 

            

 

3.2. TRAPEZIUM BENZENOID SYSTEM

For  and , let  be the trapezium benzenoid system. The definition of   should be clear from the example  shown in Figure 2, Klavˇzar (1997).

Figure 2

                                                        

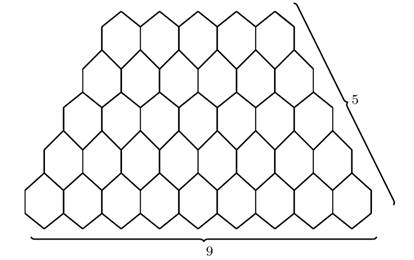
Figure 2  Trapezium Benzenoid System

 

Theorem 3.2.  Let  be two integers with  and  . Let  be the trapezium benzenoid system. Then

 

                       

                                                                                                                                             

Proof. For  , we have  , and hence

 

                                                                                                                                                        

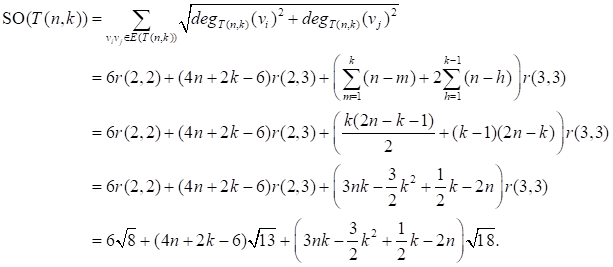
3.3. PARALLELOGRAM-LIKE BENZENOID SYSTEMS

For  and  , let  be the parallelogram-like benzenoid system of type 1. The definition of  should be clear from the example  shown in Figure 3, Klavˇzar (1997).

Figure 3

                                                              

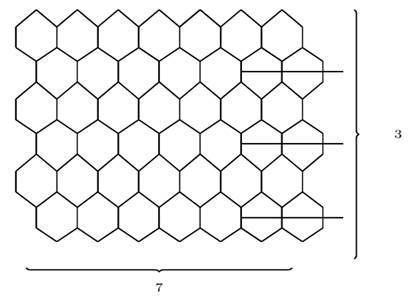
Figure 3 Parallelogram-Like Benzenoid System

 

Theorem 3.3. Let  be two integers with  and  . Let  be the parallelogram-like benzenoid system of type 1. Then

 

 

Proof. From the definition of Sombor index, we have

 

                                                                             

                                                                                                                                               

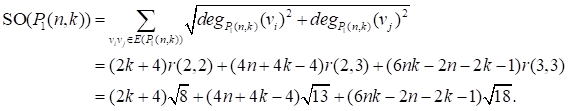
For  and , let  be the parallelogram-like benzenoid system of type 2. The definition of  should be clear from the example  shown in Figure 3, Klavˇzar (1997).

 

Theorem 3.4. Let  be two integers with  and  . Let   be the parallelogram-like benzenoid system of type 2. Then

 

                                                                                                                                             

Figure 4

                                                                    

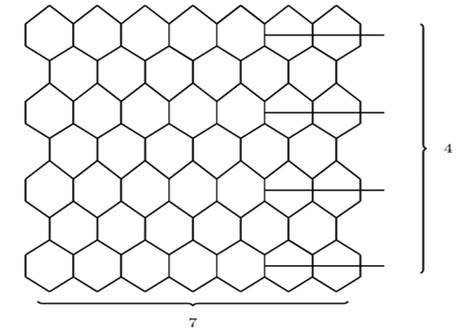
Figure 4  Parallelogram-Like Benzenoid System of

              

Proof. From the definition of Sombor index, we have

 

                                                                                                                                              

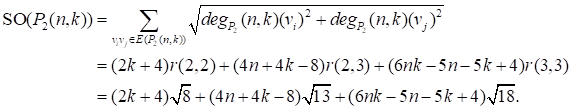
For  and , let  be the parallelogram-like benzenoid system of type 3. The definition of  should be clear from the example  shown in Figure 5, Klavˇzar (1997).

 

Theorem 3.5. Let  be two integers with  and . Let  be the parallelogram-like benzenoid system of type 3. Then 

 

                                                                                                                                                                

Figure 5

                                                                    

Figure 5 Parallelogram-Like Benzenoid System

 

Proof. From the definition of Sombor index, we have

 

                                                                                                                                            

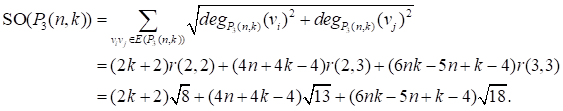
3.4.  BITRAPEZIUM BENZENOID SYSTEM

  For  ,，, and   , let  be the bitrapezium benzenoid system. The definition of  should be clear from the example  shown in Figure 6, Klavˇzar (1997).

 

Theorem 3.6.  Let  be three integers with  and ,  and  . Let  be a bitrapezium benzenoid system. Then

        

 

                          

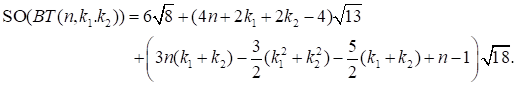
Figure 6

                                                                       

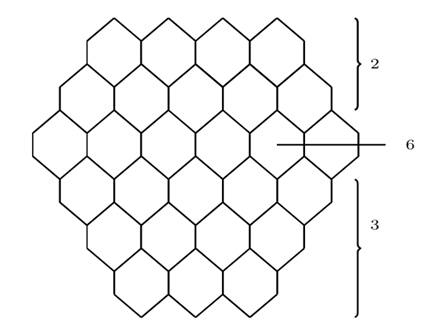
Figure 6 Bitrapezium Benzenoid System

  

Proof. From the definition of Sombor index, we have

                                                                                                                                              

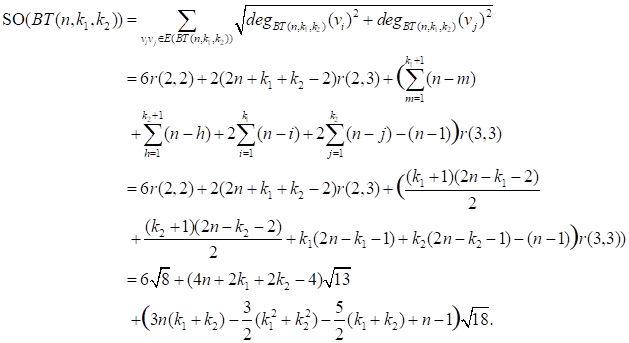
3.5.  GENERAL BENZENOID SYSTEM

For ,,, and , let  be the bitrapezium benzenoid system. The definition of  should be clear from the example  shown in Figure 7, Klavˇzar  (1997).

Figure 7

                                                                    

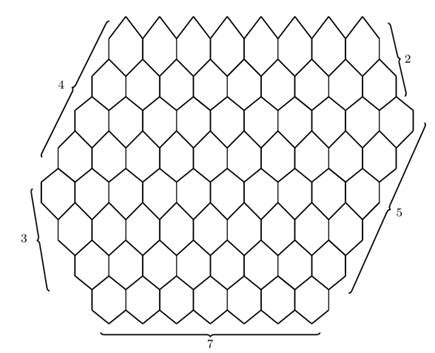
Figure 7 Bitrapezium Benzenoid System

 

Theorem 3.7. Let  be five integers with ,,  and  . Let  be a general benzenoid system. Then

 

                                                                                                                                                                                                                    

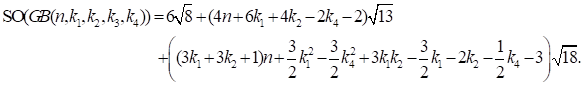
Proof. From the definition of Sombor index, we have

 

                          

 

 

                                                                                                                  

3.6.  L-POLYGONAL CHAIN

Let   A polygonal chain of  cycles (polygons) is obtained from a sequence of cycles, , by adding a bridge to each pair of consecutive cycles. If all such cycles are  -cycles, then this polygonal chain is called an  -polygonal chain of length  and denoted by. The cycle will be called the  -th polygon of . Note that, there are many ways to add a bridge between two consecutive cycles. So  may not be unique when . But  is unique when . The definition of  should be clear from the shown in Figure 8, Wei and Shiu (2019).

Figure 8

 

                                                                     

Figure 8 L-Polygonal Chain

 

Theorem 3.8.  Let  be an  -polygonal chain (of length ). Then

 

                                   

                                                                                                                                             

Proof. From the definition of Sombor index, we have

 

                                                                                                                                             

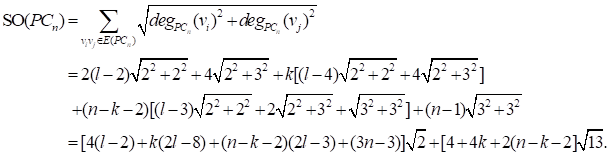
3.7. TITANIA NANOTUBES

Titania nanotubes are comprehensively studied in materials science. The  sheets with a thickness of a few atomic layers were found to be remarkably stable. Let  be the  rows and  columns of the titanium nanotubes. The definition of  should be clear from the shown in Figure 9. Imran et al. (2021).

 

Theorem 3.9. Let denote the graph of titanium nanotubes with m rows and n columns. Then

                            

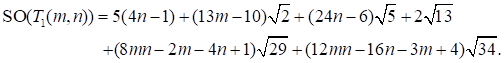
Figure 9

                                                                     

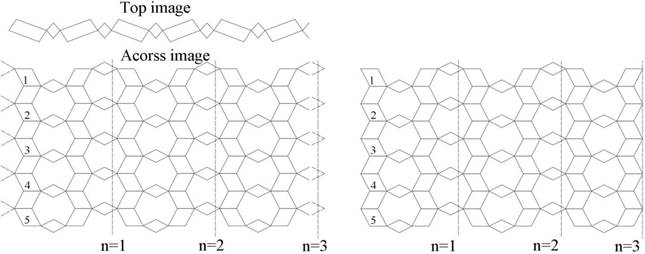
Figure 9 Titanium Nanotubes

 

Proof. From the definition of Sombor index, we have

 

.

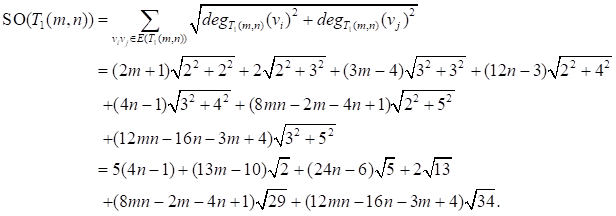CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Abdo, H., Dimitrov, D. and Gutman, I. (2019). Graph Irregularity and Its Measure.  Applied Mathematics and Computation, 357, 317–324. https://doi.org/10.1016/j.amc.2019.04.013

Albertson, M.O. (1997). The irregularity of a graph.  Ars Combinatoria, 46, 219–225. 

Balaban, A. T., Motoc, I., Bonchev, D.  And Mekenyan, O. (1983). Topological Indices for Structure-Activity Correlations. Topics in Current Chemistry, 114, 21.

Cruza, R., Gutman, I. and Rada, J. (2021).  Sombor Index of Chemical Graphs.  Applied Mathematics and Computation, 399, 126018. https://doi.org/10.1016/j.amc.2021.126018

Das, K. C., Gutman, I. (2022).  On Sombor Index of Trees.  Applied Mathematics and Computation, 412, 126575. https://doi.org/10.1016/j.amc.2021.126575

Doˇsli´ c, T., R´ eti, T. and Vukiˇ cevi´ c, D. (2011).  On The Vertex Degree Indices of Connected Graphs. Chemical Physics Letters, 512, 283–286. https://doi.org/10.1016/j.cplett.2011.07.040

Gutman, I. (2021).  Geometric Approach to Degree-Based Topological Indices : Sombor Indices.  Match Communications In Mathematical And In Computer Chemistry, 86, 11–16.

Gutman, I., Ruˇ sˇ ci´ c, B., Trinajsti, N. and Wilcox, C. F. (1975).  Graph Theory and Molecular Orbitals. XII. Acyclic Polyenes.  The Journal of Chemical Physics, 62, 3399. https://doi.org/10.1063/1.430994

Pal, M., Samanta, S. and Pal, A. (2019). Kulli, V. R. Graph Indices, In : Handbook of Research of Advanced Applications of Graph Theory in Modern Society.  Global, Hershey, pp. 66–91.

R´eti, T., T´oth-Laufer, E. (2017). On The Construction and Comparison of Graph Irregularity Indices.  Kragujevac Journal Science. 39, 53–75. https://doi.org/10.5937/KgJSci1739053R

Todeschini, R., Consonni, V. (2009). Molecular Descriptors for Chemoinformatics, Wiley–VCH, Wein-Heim.

Klavˇzar, S., Gutman, I. and Rajapakse, A. (1997). Wiener Numbers of Pericondensed Benzenoid Hydrocar-Bons, Croatica Chemica Acta 70(4), 979–999.

Wang, Z., Mao, Y., Furtula, B., and Li, Y. (2022).  On Relations Between Sombor and Other Degree-Based Indices. Applied Mathematics and Computation.  68, 1–17.

Wei, S., Shiu, W.C. (2019).  Enumeration of Wiener Indices in Random Polygonal Chains. Journal of Mathematical Analysis and Applications.  469, 537–548. https://doi.org/10.1016/j.jmaa.2018.09.027

Imran, M., Malik, M.A. and Javed, R. (2021). On Szeged-Type Indices of Titanium Oxide Tio 2 Nanotubes. International Journal of Quantum Chemistry. 121(15), E26669. https://doi.org/10.1002/qua.26669

Demirci, M., Delen, S., Cevik, A.S., and Cangul, I.N. (2021). Omega Index of Line and Total Graph. Journal of Mathematics, 09, 1–6. https://doi.org/10.1155/2021/5552202

Su, G., Xu, L. (2015).  Topological Indices of the Line Graph of Subdivision Graphs and Their Schur-Bounds.  Applied Mathematics and Computation, 253, 395–401.