ESTIMATE OF DISK NOT CONTAINING ROOTS OF POLYNOMIAL FUNCTIONS

 

Roshan Lal ¹

 

¹ Department of Mathematics V.S.K.C. Government Postgraduate College Dakpathar, Dehradun-248125, Uttarakhand, India

 

1. INTRODUCTION

If  is a   degree polynomial function, then by the Fundamental Theorem of Algebra, we know that  has at least one root in complex plane and repeated application of the theorem tells that   has exactly   roots in whole Argand plane. But the theorem, however, does not provide any information about the location of roots of a polynomial function. The issue of finding position of the roots of a polynomial function has been of great interest. This could be observed by glancing at the books of Marden (1949), Milovanovic et al. (1994), Sheil-Small  (2002) and Rahman and Schmeisser  (2002). We have also other recent articles on same area Aziz and Zargar (1966), Daras and Rassias (2015), Jain  (2009), Rahman and Schmeisser  (2002), Rassias and Gupta (2016), Shah and Liman (2007), Vieira (2017) on the subject.  Since the days of Gauss and Cauchy, many well-known mathematicians have contributed to the further growth of the subject. Here we first mention the following result of Cauchy Aziz and Mohammad (1984) that is commonly popular as Cauchy’s Theorem.

Theorem A.  If  be polynomial function, then all the roots of lie in

                                

                                                                                                      Equation 1

were

 

                    

 

Next elegant result that is commonly famous as Enestrom-Kakeya Theorem, and firstly proved by Enstrom Enestrom (1920) and later independently by Kakeya Kakeya (1912) and Hurwitz (1913).

Theorem B.  If  is a polynomial of degree n, such that

 

                                                                   Equation 2

 

then   has no roots in

In the same sphere Aziz and Zargar (1966), Aziz and Mohammad (1984), Dichler  (1996), Lal et al. (2011), Lal  (2019) there exist various generalizations and refinements of Theorem B and other related results.

Joyal et al. (1967) augmented Theorem B for the polynomial function having coefficients having all real values. More precisely, they gave the next result.

Theorem C. If  is a polynomial function of degree n, with property

 

                                                                            Equation 3

 

then all roots of  are contained in

 

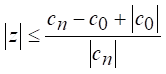                                                                                           Equation 4

 

If  then this result reduces to Theorem B.

Aziz and Zargar (1966) improved upon the bound in Theorem C.

 

Theorem D.  If  is a polynomial function of nth degree, such that for some

 

                                                                         Equation 5

                          

then all roots of   are contained in 

 

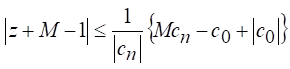                                                              Equation 6

 

Rather (1998) augmented the above Theorem D in following.

Theorem E. If  is a polynomial function of nth degree, and for some

 

           Equation 7

                                                     

Then  contains all its roots inside

 

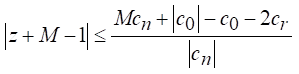                                                            Equation 8

 

2. MAIN THEOREM

The main idea of this paper is to find a region having any roots, inside the disk containing every root. Here, we are able to find such region by proving next result that gives us a root-free region for the polynomial, whose coefficients follow a certain pattern. This result improves upon the result of Enestrom and Kakeya and also some of the other results in this sphere.

 

  Theorem 2. 1.. If  be a polynomial function of nth degree, and for some   together with

                                                                                                                                    Equation 9

                                                     

then no roots of    are contained in 

 

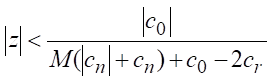                                                                 Equation 10

 

Remark 2.2. For M=1 the above result improves upon Theorem E due to Rather Rather (1998) and for ,  the above result improves upon Theorem C due to Joyal et al. (1967). Furthermore, the result proved here also refines upon the result of Enestrom-Kakeya Enestrom (1920) for   

 

3. PROOF OF MAIN THEOREM

We prove the main Theorem 2.1 as follows.

 

Proof of Theorem 2.1.

  For the proof of our main theorem, we take a new polynomial function as

 

          

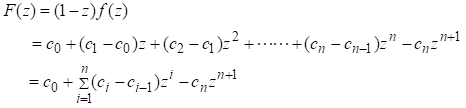
or

             

                        say                                                               Equation 11

were

                                                           Equation 12

 

From  Equation 11

                               

                    for                                                   Equation 13

 

Also, for , from Equation 12, we have

                 

 

               

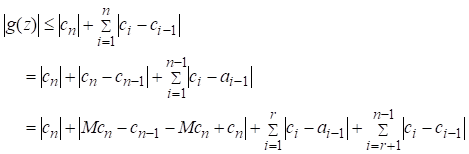
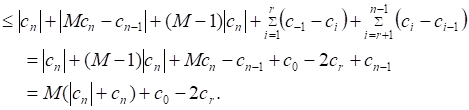
Thus for  ,

                          

                     

 

Now g (0) =0 and g(z) are analytic, we have, obviously by Schwarz’s lemma for  ,

 

                                                             Equation 14

 

Associating the Equation 13 and Equation 14, we get

 

                    

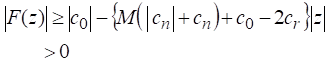
if     

                     

                         

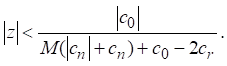
This implies that and hence  does not vanish in

 

                                           

 

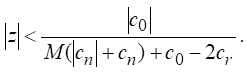
Thus, we completed the proof of Theorem 2.1.

 

4. CONCLUSION

Our result gives a circular region containing no roots or zeros of polynomial functions inside it while other mentioned earlier proved results give circular regions containing all roots. Thus, we have obtained an annular region containing all roots of polynomial the region containing all roots of polynomial function has been reduced in size. So, our result improves the estimate of region having all roots.

 

 

 

ACKNOWLEDGEMENT

The author is grateful to anonymous referee for reviewing the manuscript and giving advice.

 

REFERENCES

Aziz, A. and Mohammad, G.Q. (1984). Zero free regions for polynomials and some generalizations of Enestrom-Kakeya Theorem, Canad. Math. Bull., 27, 265-272. https://doi.org/10.4153/CMB-1984-040-3

Aziz, A. and Zargar, A. B., (1966). Some extensions of -Kakeya Theorem, Glasnik Mate., 51, 239-244.

Cauchy, A.l. (1829). Exercises de mathematique in oeuvres, Hachette Livre - BNF, 9, 122.

Daras, N. J. and Rassias, Th. (2015). Computation, Cryptography, and Network Security, Springer. https://doi.org/10.1007/978-3-319-18275-9

Dichler, K. (1996). A generalization of the Enestrom-Kakeya Theorem, Journal of Mathematical Analysis and Applications, 116, 473-488. https://doi.org/10.1016/S0022-247X(86)80012-9

Enestrom, G. (1920). Remarquee sur un Theoreme relatif aux racines de I' equation ou tous les coefficients sont reels et possitifs, Tohoku Mathematical Journal, 18, 34-36.

Hurwitz, A. (1913). Uber einen Satz des Herrn Kakeya, Tohoku Mathematical Journal, First Series, 4, 29-93.

Jain, V. K. (2009). On the zeros of polynomials, Proceedings - Mathematical Sciences, 119(1), 37-43. https://doi.org/10.1007/s12044-009-0004-5

Joyal, A. Labelle, G. and Rahman, Q. I. (1967). On the location of zeros of polynomials, Canad. Math. Bull., 10, 53-63. https://doi.org/10.4153/CMB-1967-006-3

Kakeya, S. (1912). On the limits of the roots of an algebraic equation with positive coefficients, Tohoku Mathematical Journal, First Series, 2, 140-142.

Lal, R.  Kumar, S. and Hans, S. (2011). On the zeros of polynomials and analytic functions, Annales Universitatis Mariae Curie- Skłodowska, 2011 https://doi.org/10.2478/v10062-011-0008-3

Lal, R. (2019). Results for zeros of polynomial and analytic function, Jnanabha, 49(2), 15-21.

Marden, M, (1949). Geometry of the zeros of the polynomials in a complex variable, American Mathematical Society.

Milovanovic, G. V.   Mitrinovic, D. S. and Rassias, Th. M. (1994). Topics in polynomials, Extremal properties, Inequalities, Zeros., World Scientific Publishing Co. Singapore https://doi.org/10.1142/1284

Rahman, Q. I. and Schmeisser, G.  (2002). Analytic Theory of Polynomials, Clarendon Press. Oxford.

Rassias Th. M. Gupta, V. (2016). Mathematical Analysis, Approximation Theory and Their Applications, Springer Nature. https://doi.org/10.1007/978-3-319-31281-1

Rather, N. A. (1998). Extremal properties and location of zeros of polynomials.

Shah, W. M. and Liman, A. (2007).  On Enestrom-Kakeya Theorem and related analytic functions, Proc. Proceedings Mathematical Sciences, 117 (3), 359-370. https://doi.org/10.1007/s12044-007-0031-z

Sheil-Small, T. (2002). Complex polynomials, Cambridge Univ. Press.

Vieira, R. S. (2017). On the number of roots of self-inversive polynomials on the complex unit circle. The Ramanujan Journal.  42(2),363-369.