|
|
|
|
Article Type: Research Article
Article Citation: Rwabi AzZwideen, and Loai M. Al-Zou’bi. (2020). THE TRANSMUTED GAMMA-GOMPERTZ DISTRIBUTION.
International Journal of Research -GRANTHAALAYAH, 8(10), 236 - 248. https://doi.org/10.29121/granthaalayah.v8.i10.2020.1892
Received Date: 04 October 2020
Accepted Date: 31 October 2020
Keywords:
Transmuted Gamma-Gompertz Distribution
Moments
Skewness
Reliability
Hazard Rate Function
Kurtosis
Entropy
Order Statistics
Quantile Function
Median
ABSTRACT
This article introduces a four-parameter probability model which represents a gener- alization of the the Gamma-Gompertz distribution using the quadratic rank trans- mutation map. The proposed model is named the Transmuted Gamma-Gompertz distribution. We provide explicit expressions for its statistical properties, moment generating function, quantile function, the order statistics, the quantile function and the median. We estimate the parameters of the distribution using the maximum likelihood method of estimation.
1. INTRODUCTION
In probability and statistics, the Gamma-Gompertz distribution is continuous proba- bility distribution, it has been used as an aggregate-level model of customer lifetime and a model of mortality risks. if X denotes a random variable, the cumulative density function (CDF) and the probability density function (pdf) of the Gamma- Gompertz distribution with b a scale parameter, and s, β are shape parameters, are respectively given by;
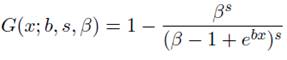 (1)
(1)
 (2)
(2)
Where x >0, the scale parameter b>0 and the shape parameters s, β>0.
If β = 1, the distribution reduces to the exponential distribution with parameter
sb.
Shaw07 studied the quadratic rank transmutation map (QRTM) and in recent times, several authors have used the understanding to generalize several known the- oretical models. For instance, aryal13 generalized the Weibull distribution using the QRTM and named the resulting distribution the Transmuted Weibull distribution. In the same manner, the Transmuted Rayleigh distribution by merovci13, Trans- muted Exponentiated Modified Weibull Distribution by ashour13, Transmuted Mod- ified Weibull distribution by khan, Transmuted Lomax distribution by cord, Trans- muted Exponentiated Gamma distribution by hussian, Transmuted Inverse Rayleigh distribution by ahmad, Transmuted Pareto distribution by puka, Transmuted New Modified Weibull distributions vardhan16. Transmuted Inverse Exponential Distri- bution by ognto. alzoubi proposed Transmuted Mukherjee-Islam distribution as a generalization of Mukherjee-Islam distribution.
2. THE TRANSMUTED GAMMA-GOMPERTZ DISTRIBUTION
Starting from an arbitrary parent cumulative density function G(x), a random vari- able X is said to have a transmuted distribution if its CDF is given by;
![]() (3)
(3)
Deriving Equation (3) with respect to x, we get
![]() (4)
(4)
Where |λ| ≤ 1, g(x) and f (x) are the associated pdf of G(x) and F (x) respectively. Notice that if λ = 0; Equations (3) and (4) reduce to the parent distribution. Hence, a random variable X is said to have a Transmuted Gamma-Gompertz distribution with parameters b, s, β and λ if its cumulative density function is given by:
 (5)
(5)
The corresponding pdf is given by;
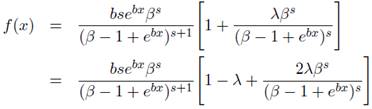 (6)
(6)
for x > 0, b, s, β>0 and |λ| ≤ 1.
Where b is the scale parameter, s, β are shape parameters, λ is the transmuted parameter.
For s = 1 and β = 1, this distribution reduces to Transmuted Exponential Distribution.

Figure 1: The pdf and the CDF of the TGG random variable with λ = −1, −0.5, 0, 0.5, 1, b = s = 2 and for different values of β.
3. RELIABILITY ANALYSIS
In this sub-section, we present the reliability function and the hazard function for the proposed TGG distribution. The reliability function is otherwise known as the survival or survivor function. It is the probability that a system will survive beyond a specified time and it is obtained mathematically as the complement of the cumulative density function (CDF). The survivor function is given by;
![]()
Hence, we present the reliability function of the TGG distribution as:
![]()
The hazard function is otherwise known as the hazard rate, failure rate, or force of mortality. It is obtained mathematically as the ratio of the probability density function f (x) to the survival function S(x).
![]()
We thus present the hazard rate for the proposed TGG distribution as;

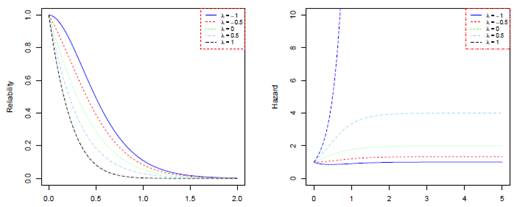
Figure 2: The reliability and hazard functions of the TGG random variable when λ = −1, −0.5, 0, 0.5, 1, b = s = 2 and for different values of β.
4. MOMENTS AND ASSOCIATED MEASURES
This section provides some of the statistical properties of the TGG distribution.
4.1. MOMENTS
Let X be a TGG distribution. Then the rth moment of X, E(Xr); is defined as
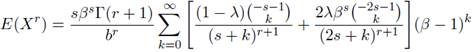 (7)
(7)
![]()


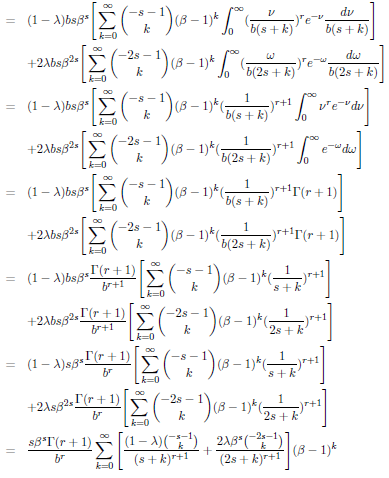
Therefore, the first and the second moments, E(X) and E(X2), are computed by substituting r = 1 and 2 in Equation (7). The two moments and the variance, var(X) are; respectively, given by:
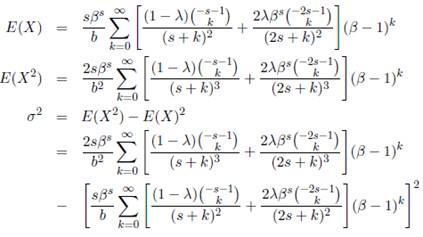
4.2. COEFFICIENT OF VARIATION
The coefficient of variation (CV) is the ratio of standard deviation ((σ) to mean (µ). The main purpose of finding is used to study of quality assurance by measuring the dispersion of the population data of a probability or frequency distribution, or by determining the content or quality of the sample data of substances. The method of measuring the ratio of standard deviation to mean is also known as relative standard deviation often abbreviated as RSD. It only uses positive numbers in the calculation and expressed in percentage values. Therefore, the resultant value of this formula CV
= (Standard Deviation (σ) / Mean (µ)) will be multiplied by 100. CV is important in the field of probability and statistics to measure the relative variability of the data sets on a ratio scale. In probability theory and statistics, it is also known as unitized risk or the variance coefficient.


4.3. SKEWNESS AND KURTOSIS
A fundamental task in many statistical analyses is to characterize the location and variability of a data set. A further characterization of the data includes skewness and kurtosis. Skewness is a measure of symmetry, or more precisely, the lack of symmetry. A distribution, or data set, is symmetric if it looks the same to the left and right of the center point.
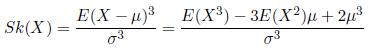

Kurtosis is a measure of whether the data are heavy-tailed or not. That is, data sets with high kurtosis tend to have heavy tails, or outliers. Data sets with low kurtosis tend to have
Table 1: The mean, standard deviation, skewness, kurtosis and the coefficient of variation of the TGGD random variable for different values of λ when b = s = β = 2
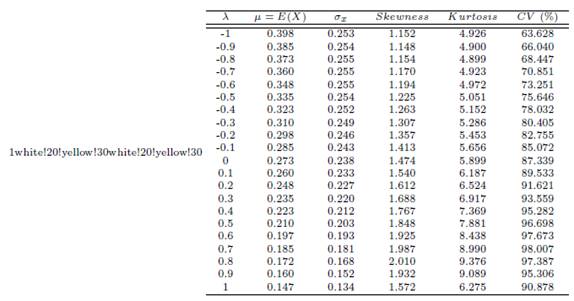
light tails, or lack of outliers.

4.4. MOMENT GENERATING FUNCTION
Let X be a TGG random variable. Then the moment generating function (mgf) of a random variable X, MX (t) is given by:

proof:

4.5. THE QUANTILE FUNCTION AND MEDIAN
The Quantile Xq of the TGGD is the real solution of the equation;
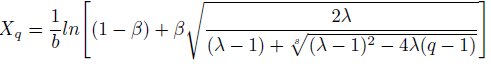
proof:

By solving this equation with respect to γ, we get:
 (9)
(9)
from 8 and 9
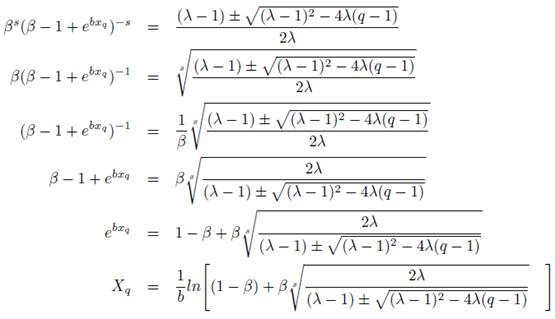
Hence, the median of the distribution is derived by substituting q= 0.5 in the equation. That is,
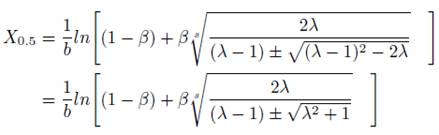
5. MAXIMUM LIKELIHOOD ESTIMATION
The maximum likelihood estimates, MLEs, of the parameters that are inherent within the TGG distribution function is given by the following: Let X1, X2, . . . , Xn be a sample of size n from a TGG distribution. Then the likelihood function is given by:

![]()
Hence, the log-likelihood function = lnL become

Therefore, the MLEs of b, s, β and λ which maximize (10) must satisfy the following normal equations:

The maximum likelihood estimator θˆ = (ˆb, sˆ, βˆ, λˆ) of θ = (b, s, β, λ) is obtained by solving this nonlinear system of equations.
6. ORDER STATISTICS
In statistics, the kth order statistic of a statistical sample is equal to its kth smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non- parametric statistics and inference. For a sample of size n, the nth order statistic (or largest order statistic) is the maximum, that is X(n) = max X1, X2, . . . , Xn . The sample range is the difference between the maximum and minimum. It is clearly a function of the order statistics Range {X1, X2, . . . , Xn} = X(n) − X(1). We know that if X (1) ≤ X (2) ≤ . . . ≤ X(n) denotes the order statistics of a random sample X1, X2, . . . , Xn from a continuous population with CDF FX (x) and pdf fX (x) then the pdf of X(j) is given by:
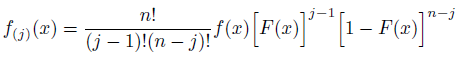
forj = 1, 2, . . . , n.
The pdf of the kth order statistic for TGG distributions is given by:
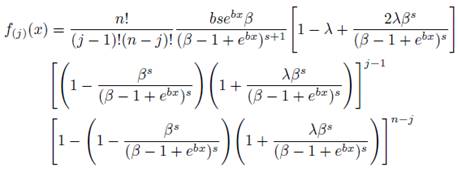
Therefore, the pdf of the largest order statistic X(n) is given by

and the pdf of the smallest order statistic X (1) is given by
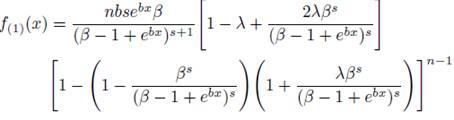
7. ENTROPY
Given a sample of probabilities pi,
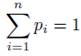
The R’enyi Entropy renyi of the sample is given by:
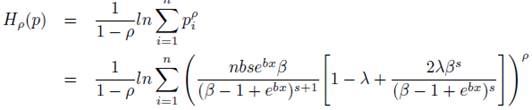
The R’enyi entropy tends to Shannon entropy shanon as ρ −→ 1.

SOURCES OF FUNDING
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
CONFLICT OF INTEREST
The author have declared that no competing interests exist.
ACKNOWLEDGMENT
None.
|
|
 This work is licensed under a: Creative Commons Attribution 4.0 International License
This work is licensed under a: Creative Commons Attribution 4.0 International License
© Granthaalayah 2014-2020. All Rights Reserved.


