Article Citation: Keval D. Vyas, Jeel A. Anovadia, and Dr. Ashutosh K. Patel. (2021). MODIFIED EFFECTIVE AREA APPROACH TO ESTIMATE MOTORCYCLE EQUIVALENT UNITS IN AHMEDABAD CITY. International Journal of Engineering Technologies and Management Research, 8(4), 6-16. https://doi.org/10.29121/ijetmr.v8.i4.2021.904

 

Published Date: 12 April 2021

 

Keywords:

Motorcycle Equivalent Unit

Mixed Traffic

Urban Road

Effective Area

Ahmedabad City
ABSTRACT

This paper presents a methodology for estimation of Motorcycle Equivalent Units (MEU) in mixed traffic flow for motorcycle dominated traffic with increased accuracy by considering dynamic characteristics of subject vehicles, like speed and effective area. Besides, this increased accuracy is the result of the inclusion of speed of adjacent motorcycles in the form of speed ratios to estimate the effective area required by the subject vehicle at a particular speed. The effective area for each sample is computed with consideration of the effective dimensions and speed of that subject vehicle and its adjacent motorcycles on both sides in the proposed methodology. Two mid-block sections of urban roads in Ahmedabad city were selected for field data collection by videography method in this case study. The collected field data was analysed through Speed Estimation from Video Data (SEV) software. A table of classified speed ratios is also presented to derive an idea regarding the magnitude of change in lateral clearances of subject vehicles. The MEU values obtained for cars, motorcycles, rickshaws, buses, Light Commercial Vehicles (LCV), and bicycles were 3.02, 1.00, 1.84, 9.82, 6.2, and 1.9 respectively. Further, the proposed model was compared with a previously developed model to justify the increase in accuracy and to observe the variations in MEUs. The values estimated can be used to establish speed-flow relations, measure roadway capacity in urban roads, analyse the level of service in order to plan suitable traffic control and regulatory measures.

1.     INTRODUCTION

 

In Ahmedabad, total registrations of the two-wheeler vehicles (since 2005) as of November 2020 were recorded 1,948,844 units as opposed to cars recorded as only 594,679, wherein motorcycles being more than thrice the number of cars. The growth rate in registrations of two-wheelers in 2019-2020 was 14.93% and that of cars was -0.94%, which indicates the rise in ownership of two-wheeler vehicles in Ahmedabad city.[1]It has been observed that registrations of two-wheeler vehicles in the city are increasing annually since the year 2000. Reasons contributing to this are its affordability, high mileage, economical maintenance, manoeuvrability, etc. In general, total traffic in Ahmedabad comprises about 70% of two-wheeler vehicles. The concept of Passenger Car Equivalent (PCE) was introduced in Highway Capacity Manual in 1965 and since then, a lot of research has been conducted for estimating PCE or Passenger Car Unit (PCU) values for different roadway conditions. However, PCU values are not suitable in Indian urban roads due to the heterogeneous mix of traffic, absence of lane discipline, and predominance of two-wheelers.

Traffic condition in India is very different from the developed countries. The latter is dominated by passenger cars which can be termed as almost homogeneous traffic, whereas the former is composed of different classes of vehicles, particularly in urban roads, dominated by motorcycles (a majority in the range of 100cc to 150cc). In this context, the category of motorcycles is comprised of geared bikes, electric bikes, non-geared scooters, geared scooters, and mopeds. There exists a wide range of static and dynamic characteristics in vehicles on roads occupying the same right of way; thus, resulting in an “unsynchronized movement” (Sai Kiran and Verma 2016). Most of the studies are carried out in developed countries, and there exist fewer studies taking into consideration the mixed nature of traffic as observed in India. While dealing with traffic comprising of different vehicle types such as motorized two wheelers, motorized three wheelers and non-motorized vehicles, it is thus essential to include area of the vehicle to represent the realistic traffic behaviour (Mallikarjuma and Rao 2006). Very little research work has been done to include the influence of adjacent vehicles in the estimation of area occupancy of subject vehicles.

It appears more relevant to use a motorcycle as the base vehicle for equivalency factors. The dominance of motorcycles in a traffic flow affects the traffic condition differently than passenger cars. Due to their easy maneuverability, “motorcycles may reduce the speed of other modes and make the traffic congested owing to their superiority in numbers” (Minh et al. 2005). Further, the smaller size of motorcycles reflects “gap-filling” behaviour rather than the “car-following” behaviour. The problem of measuring the traffic capacity of roads with mixed nature of traffic is often resolved by converting all classes of vehicles into a common equivalent unit.

The objective of this study is to propose a modified methodology for the estimation of motorcycle equivalent units for all the classes of vehicles for mixed traffic flow with speed and effective area parameters. Effective area is the area required by a vehicle to maintain its desired speed on a road. Moreover, this study also compares the results with an existing method that does not consider the speed of adjacent motorcycles in its model.

 

1.1. LITERATURE REVIEW

 

Passenger car equivalents have been determined by various methods, like the headway method, the multiple linear regression method, the simulation method, the modified density method, etc. Nevertheless, there is no “correct” method to estimate PCUs, but each method helps in understanding the effects of the subject vehicle on traffic from a different perspective (Sai Kiran and Verma 2016). Moreover, The Indian Road Congress IRC 106-1990 recommends PCU factors for various types of vehicles on urban roads in India, which are widely adopted in Indian urban road conditions.

Chandra and Kumar (2003) estimated the values of PCU for various classes of vehicles in mixed traffic conditions in India. Mean speed and their respective projected area on the ground were used in their model for estimating PCU values. PCU values for different vehicles under mixed traffic situations are directly proportional to the speed ratio and inversely proportional to the space occupancy ratio with respect to passenger cars (Chandra and Kumar 2003).

 

                                                                                                                                                                                                               (1)

 

Where, V_c and V_i = mean speed for cars and type i vehicles respectively, and A_c  and A_i = their respective projected rectangular areas (length ×width) on the road. Nonetheless, projected areas here are static values, but in the actual scenario, the area requirement by each vehicle on road depends on several factors such as speed of the subject vehicle, speed of the surrounding vehicles, driver characteristics, etc.

Lan and Chang (2003) developed a particle-hopping model with Cellular Automata to describe the motorcycles’ behaviour in a mixed traffic flow with cars and motorbikes on 2.5m and 3.75m lanes in Taipei. In their findings, the motorbike equivalents ranged from 2.63 to 5.27 for 10%~100% of car mixes. For motorcycle equivalent units, Minh et al. (2005) provided a thorough analysis of motorcycle behaviour and operation by videography method on a few of the roads having significant motorcycle proportion in Hanoi, Vietnam; even so, the limitations of this study were the same as in Chandra and Kumar (2003). Moreover, Cao et al. (2007) studied the impacts of effective spaces on speeds of various vehicles. The effective space approach is used here instead of the projected area to estimate Dynamic Motorcycle Unit (DMCU) values. The relationship between speed and effective space for each class of vehicle is established for three locations in Hanoi city, Vietnam. Nguyen and Montgomery (2007) applied the concept of Motorcycle Units (MCU) at signalized intersections in Hanoi city, Vietnam. They examined the variation of saturation flow and vehicle equivalency factors in motorcycle dominated traffic conditions.

Furthermore, Asaithambi and Mahesh (2016) adopted a similar methodology for urban roads in India using the effective space approach. The study was conducted on mid-block sections of four-lane divided urban roads in Chennai and Mangalore and these values were validated with previously developed methods. Prahara et al. (2018) analysed the traffic in Jakarta for MCU values with the effective space approach similar to Asaithambi and Mahesh (2016).

Cao and Sano (2012) modified the method for estimating more accurate values of MEUs in mixed traffic flow considering the characteristics of moving vehicles, such as speed and effective space. It was suggested that the effective space is affected by size of the subject vehicle and motorcycles on its left and right side; hence, it was assumed that the lateral width of subject vehicle is a function of the lateral width of motorcycles and the total physical size of subject vehicle and motorcycles. Pooja et al. (2018) adopted the effective area approach to estimate dynamic PCU values for mixed traffic conditions in India. Six distinct cases were considered on a roadway for estimation of effective areas. Lateral clearance between the subject vehicle and adjacent vehicles was distributed using the similar method as in Cao and Sano (2012) i.e. by size ratio. Srikanth (2019) used space occupancy method to estimate dynamic PCUs in Ongole city. The space headway obtained for each vehicle for a particular speed range was added to the length of the vehicle to obtain effective length of the vehicle; however, 1.1 times the width of the vehicle was assumed to be the effective width.

As of above, these methods for estimation of MEUs use a similar equation that is modified from the model of Chandra and Kumar (2003) for estimation of PCU values which considers the area occupancy criteria in its model. Nevertheless, efforts have been made previously to determine the area occupancy with different approaches with a view to estimating it accurately to the corresponding speed of the vehicle. Therefore, this paper will support the estimation of the effective area of the subject vehicle with the inclusion of the speeds of adjacent motorcycles to the subject vehicle and compare the parameters obtained with previous method by Cao and Sano (2012) employed in the estimation of MEUs for mixed traffic conditions dominated by motorcycle traffic as in Indian urban roads.

 

2.     MATERIALS AND METHODS

 

“The definition of an MEU is the number of motorcycles that can be displaced for one vehicle of a specified type running at the speed of that vehicle” (Cao and Sano 2012). The modified equation adopted by Cao and Sano (2012) was adopted here to estimate MEUs.

 

                                                                                                                                                                              (2)

 

Where, MEU_k = MEU of type k vehicle; _mc, _k= mean speed of motorcycles and type k vehicle respectively in (m/s) and _mc, _k= mean effective area for motorcycles and type k vehicle respectively in (m²).

The effective area required by a vehicle moving at a certain speed is assumed to be an imaginary rectangle formed around the subject vehicle in order to maintain its speed. This area is considered to be dynamic, and it depends on the speed and size of the subject vehicle and adjacent motorcycles, driver characteristics, etc. The effective area of a subject vehicle is illustrated with a bold line in figure 1, where surrounding vehicles are considered as motorcycles.

From figure 1,

Effective area S_k = L_e × W_e

Where,

Effective length, L_e= Length of subject vehicle L + Head clearance H_c

Effective width, W_e = D_k(L) + D_k(R) + Width of subject vehicle W

D_k(L) = Part of lateral clearance on left side for subject vehicle     

D_k(R) = Part of lateral clearance on right side for subject vehicle

 

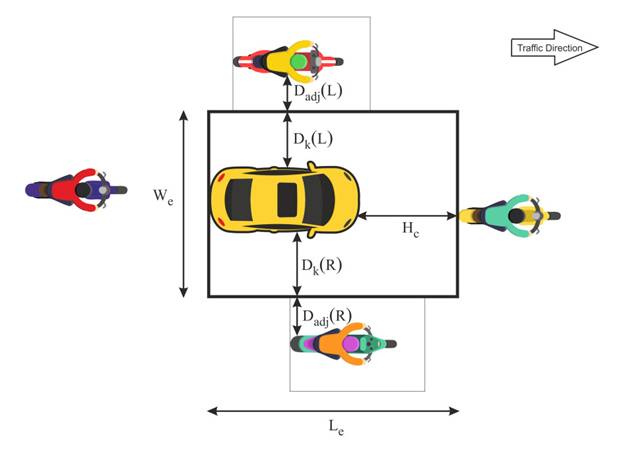
Figure 1 :  Effective Area of a Subject Vehicle

 

Effective length (L_e) can be calculated simply by addition of head clearance (H_c) to the average length of the subject vehicle, whereas the measurement of effective width poses a problem as it differs for each vehicle under consideration because there are certain factors making it dynamic. Particularly, the values of D_k(L) and D_k(R) are variable factor for each sample. “In fact, the occupied space of a vehicle is affected by the size of the subject vehicle and the motorcycles on its right and left side” (Cao and Sano 2012). In addition to the size ratio, the speeds of adjacent motorcycles of the subject vehicle have been considered in this methodology by incorporating speed ratio (V_k/V_adj). Only those samples with motorcycles as surrounding vehicles have been considered because the traffic is motorcycle dominated; further, consideration of other categories as adjacent vehicles will disrupt the uniformity in effective area calculation by changing the size ratio for distribution of lateral clearance. It is assumed that the lateral clearance of a subject vehicle is the function of lateral clearance of the adjacent motorcycle and the physical sizes of subject vehicle and adjacent vehicles along with their corresponding speeds. Therefore, the equation to determine the lateral clearances is obtained as follows:

 

                                                                                                                                                            (3)

 

Where,

D_k = Part of lateral clearance for the subject vehicle from the total lateral clearance.

D_adj = Part of lateral clearance for adjacent motorcycle from the total lateral clearance.

L_k, W_k = Physical length and width as projected area of subject vehicle.

L_adj, W_adj = Physical length and width as projected area of adjacent motorcycle.

V_k, V_adj = Speed of subject vehicle and adjacent motorcycle respectively.

D = Overall lateral clearance

From figure 1,

 

                                                                                                                                                                                            (4)

 

 

Substituting equation (3) in (4),

 

                                                                                                                                                                (5)

 

Substituting equation (5) in (4),

 

                                                                                                                                                                 (6)

 

Equation (6), is applied to calculate the values of lateral clearances for subject vehicle i.e. D_k(L) and D_k(R). The average vehicle dimensions of various categories of vehicles are adopted from Chandra and Kumar (2003) since they have been used in the studies of various developing countries with mixed traffic and are suitable to Indian conditions. Traffic in Ahmedabad city is mixed in its nature; it is imperative to identify all the classes of vehicles present at the study location in considerable proportion. Hence, the mentioned classes and types of vehicles in table 1 were recognized after the classified volume study and only those classes were included for data analysis.

 

Table 1: Average Vehicle Dimensions

 

2.1. DATA COLLECTION

 

Primarily, the site selection criteria were determined and the ideal sites were selected based on compliance with these criteria. Following criteria were used to identify appropriate road stretch in Ahmedabad city:

·        Both the ends of trap length fairly away from any intersection or diversion.

·        Presence of a high building to mount video camera setup.

·        Minimum obstruction to traffic flow due to speed breakers, parking, bus stops etc.

·        Major urban road with high traffic volume during peak hours.

·        Considerably mixed traffic with adequate percentage of motorcycles.

·        Plain gradient and fairly straight road.

 

Two mid-block sections were selected in Kalupur and Nikol, Kalupur Road (Kalupur Railway Station to Kalupur Darwaja) and Nikol Road (Thakkarbapa Nagar Flyover to Nikol Lake). Both of these road stretches were two-lane roads in the direction of traffic being studied. The data was collected by adopting videography method in dry weather and during evening peak hours i.e. 5:45-8:15 p.m. on a working weekday. Motorcycles were found to be dominating in their proportion in the traffic flow at both sites. The data collection was performed by use of a video camera mounted on a tripod on the fourth floor of a building in the vicinity of the road. A trap length of 25m was considered on the road stretch. The data required for further analysis consists of classified volume count of traffic, speed and effective area of various samples, and road measurements.

 

 

 

 

 

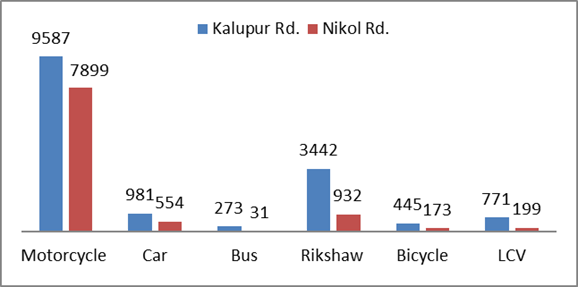
Figure 2 : Traffic Composition at both study locations

 

2.2. DATA ANALYSIS

 

To analyse the traffic data collected in the video format, software namely SEV.exe was utilized. This software was developed in the traffic laboratory for this specific purpose as described in Minh et al. (2005) Four base points i.e. four corners of the trap length on the road stretch are to be marked; it gives readings for speed and distance co-ordinates for each sample vehicle. Also, it easily converts screen co-ordinates into roadway co-ordinates, which are useful in calculating effective area around the subject vehicle. Any reading can be measured several times; thus, it can be verified. The speed of each sample vehicle was calculated at 0.5 sec interval.

 

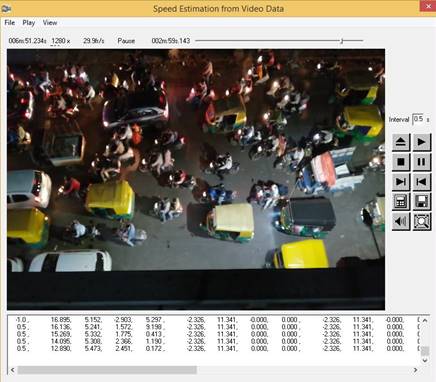
Figure 3: SEV software screen

 

3.     RESULTS AND DISCUSSIONS

 

From the data of speeds and effective areas of each category of vehicles, a graph showing the relationship between these two variables has been plotted. Non-linear equations with coefficients of determination between these variables are also expressed by non-linear regression analysis for all the categories of vehicles at both locations. Further, there are two graphs plotted for each category of vehicles to compare the existing method by Cao and Sano (2012) to the proposed method for estimating effective areas.

 

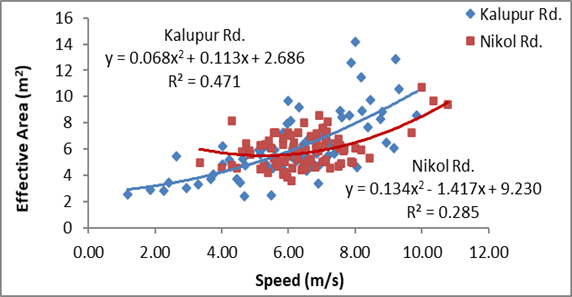
Figure 4: Relation between speeds and effective areas for motorcycles by existing method

 

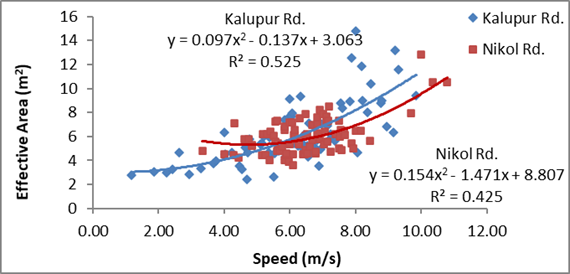
Figure 5: Relation between speeds and effective areas for motorcycles by proposed method

 

The association of speeds of motorcycles with their corresponding effective areas has increased when effective areas are estimated with inclusion of speeds of adjacent motorcycles, from figure 4 and 5. This increase in their relationship can be noted by the increase in the coefficient of determination by the proposed method. The R² value for Nikol road is comparatively less and the reason for this can be seen in figures 4 and 5; there is a scattered cluster of readings of effective areas in a small range of speeds unlike in Kalupur road, where the readings of effective areas are distributed in a comparatively larger range of speeds.

 

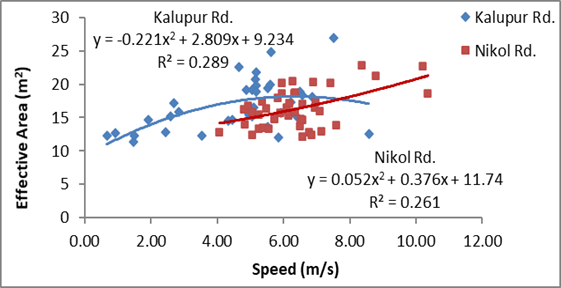
Figure 6: Relation between speeds and effective areas for cars by existing method

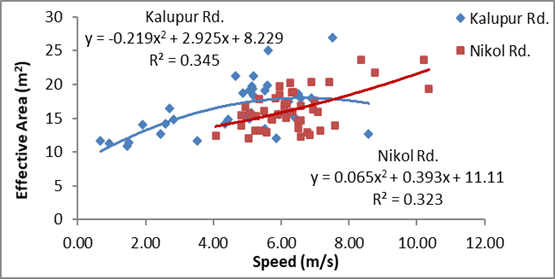
Figure 7: Relation between speeds and effective areas for cars by proposed method

 

From figures 6 and 7, similar to motorcycles, there is a fair increase in the correlation between both variables by proposed method. Further, the variation in average prevailing speed of cars at both locations can be noticed from the graphs.

There is a significant increase in R² values for rickshaws by proposed methodology, from figures 8 and 9. Also, the high number of rickshaws at Kalupur road can be attributed to the presence of a major railway station and high population density at the location. The gap in speed range of rickshaws at Nikol road can be observed in the figure. The reason for this may be attributed to the time at which the samples were observed i.e. peak hour and off-peak hour.

 

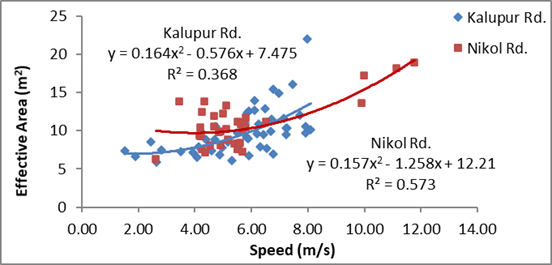
Figure 8: Relation between speeds and effective areas for rickshaws by existing method

 

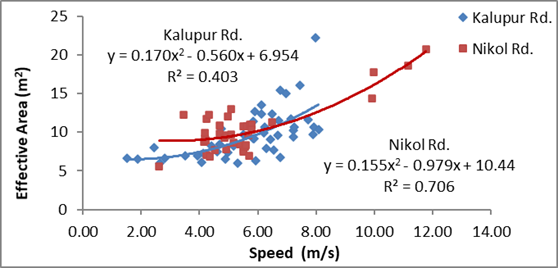
Figure 9: Relation between speeds and effective areas for rickshaws by proposed method

Table 2: Relationship summary of bus, LCV, and bicycle

                         *By existing methodology of Cao and Sano (2012)

 

Figures of the relationship between the speeds and the effective areas for buses, LCVs, and bicycles are not illustrated in this paper. Therefore, a brief summary of their relationship by the proposed method is given in table 2. From these relationships, it can be observed that there is a fair increase in R² values in every category by the proposed methodology, which indicates that the association of speeds with effective areas has increased by this method and that the speed of adjacent motorcycles affect the effective area, and it should be taken into account for estimation of dynamic MEUs. Even a minor increase in accuracy would result in significant variation in traffic capacity when estimated with these modified equivalency factors. Table 3 indicates the speed variations between the subject vehicle and its adjacent motorcycles by the speed ratios for each class of vehicles at both study locations. With these speed ratios, a notion of the approximate magnitude of change in lateral clearance for a subject vehicle (D_k) can be interpreted. An increase or decrease in effective areas, by the proposed method, is a result of an increase or decrease respectively in speed ratios from the numerical value ‘1’.

 

Table 3: Speed Ratios (V_k/V_adj)

 

The MEU values are estimated from the mean speed and mean effective area by equation (2). Table 4 depicts the values of MEUs for each category of vehicles at both the study locations. Also, the final MEU column presents the MEU values obtained by combining the data obtained from both locations. MEU1 and MEU2 indicate the values obtained by the existing model and proposed model respectively.

 

Table 4: Comparison of results of MEUs by existing and proposed model

 

Interestingly, the MEU values for bicycles are greater than that of the motorcycles. This is because the bicyclists usually travel near the edge of the road; therefore, the influence of motorcycles on their effective area is minuscule. In addition, when the mean speed of any subject vehicle is less and the mean effective area is more, there will be a greater MEU value. A decrease in the effective area ratio, as compared to the effective area ratio computed without consideration of speed of adjacent motorcycles, would result in a decrease in the MEU value and vice versa, from equation (2). The same explanation can be used to comprehend the extensive variation of MEU values of buses at both locations. According to the proposed method, the effective area of a subject vehicle will decrease (when compared to the existing method) if the speed of adjacent motorcycles is higher than that of the subject vehicle and vice versa; if the speed of the adjacent motorcycle is greater than the speed of the subject vehicle, it would result in a lower speed ratio (less than 1), consequently reducing the effective area, as per the proposed model, which otherwise would have been invariable to the effect of speed of adjacent motorcycles. Also, the effective area of a subject vehicle changes in the proposed model only due to a change in lateral clearance of the subject vehicle (D_k), which would depend ultimately on overall lateral clearance (D), the size ratio, and the speed ratio, from equation (6). In the case of vehicles of same class, the size ratio would be constant and a higher effective area would imply lower speed of adjacent motorcycles and/or greater overall lateral clearance (D).

Driver characteristics, traffic volume, road geometric characteristics, and other local traffic conditions may also affect the effective areas of subject vehicles, but they are not included in the scope of this study. Thus, the model can be modified further to consider these aspects so as to increase the accuracy forward. More data from different spots and a larger dataset can be incorporated for increasing the accuracy pertaining to the location under consideration.

 

4.     CONCLUSION

 

The model of estimating PCU in mixed traffic conditions was modified in previous studies to estimate the MEU of various classes of vehicles in mixed traffic conditions on urban roads. Hence, the fundamental objective of this paper is to propose a model to estimate these equivalency factors with increased accuracy by the inclusion of speeds of adjacent motorcycles around the subject vehicle. These MEU values determined can be used to estimate the capacity of urban roads with mixed traffic conditions like in Ahmedabad city by converting different classes of vehicles into a unique factor in terms of motorcycles.

There is a fair increase in the R² value for each class when effective areas are computed with the inclusion of speed of adjacent motorcycles; hence, it should be considered while estimating effective areas of a subject vehicle. The MEU values obtained from this study for cars, motorcycles, rickshaws, buses, LCVs, and bicycles were 3.02, 1, 1.84, 9.83, 6.2, and 1.9 respectively. The MEU values obtained here by the proposed model are smaller than the previous model of Cao and Sano (2012); which reveals that the ratios of mean effective area are necessarily smaller and the variation in the effective area of each sample is a direct result of speed ratios included in the model. A major limitation of the proposed methodology is that it can only be applied when the subject vehicle and the surrounding motorcycles are in motion. Moreover, the values of speeds and effective areas have been calculated from a video using SEV software and it is arduous to measure the actual values of every sample to its exactness; therefore, the relative error or the percentage error is unknown and not mentioned.

 

RESEARCH DATA

 

Vyas, Keval; Anovadia, Jeel (2021), “Effective Area Parameters”, Mendeley Data, V1, http://dx.doi.org/10.17632/v5mgr25w2n.1

 

SOURCES OF FUNDING

 

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

 

CONFLICT OF INTEREST

 

The author have declared that no competing interests exist.

 

 

ACKNOWLEDGMENT

 

We express our humble gratitude to Dr. Chu Cong Minh for providing us access to the SEV software. We are immensely thankful to Dr. Gaurang J. Joshi, Dr. Harish R. Varia, Prof. Rahul R. Sharma, and Prof. Krunal S. Patel for guiding us with their valuable feedbacks and suggestions. We also appreciate the assistance of Ahmedabad Regional Transport Office, Government of Gujarat by supporting us with the vehicle registration data of Ahmedabad city.

 

REFERENCES

 

    [1]       Asaithambi, G., & Mahesh, A. (2016, January 12). Estimation of Motorcycle Unit for Motorcycle Dominated Mixed Traffic on Urban Roads in India. Transportation Research Board 95th Annual Meeting, Washington DC.

    [2]       Cao, N. Y., & Sano, K. (2012). Estimating Capacity and Motorcycle Equivalent Units on Urban Roads in Hanoi, Vietnam. Journal of Transportation Engineering, 138(6), 776–785.

https://doi.org/10.1061/(ASCE)TE.1943-5436.0000382

    [3]       Cao, N. Y., Sano, K., & Minh, C. C. (2007). Dynamic Motorcycle Unit and Mean Stream Speed Under Mixed Traffic Conditions on Urban Roads. Journal of the Eastern Asia Society for Transportation Studies, 7, 2439–2453. https://doi.org/10.11175/easts.7.2439

    [4]       Chandra, S., & Kumar, U. (2003). Effect of Lane Width on Capacity under Mixed Traffic Conditions in India. Journal of Transportation Engineering, 129(2), 155–160.

https://doi.org/10.1061/(ASCE)0733-947X(2003)129:2(155)

    [5]       Lan, L., & Chang, C.-W. (2003). Motorbike’s moving behaviour in mixed traffic: Particle-hopping model with Cellular Automata. Journal of the Eastern Asia Society for Transportation Studies, Vol. 5, Pp. 23-37.

    [6]       Mallikarjuna, C., & Rao, K. R. (2006). Area Occupancy Characteristics of Heterogeneous Traffic. Transportmetrica, 2(3), 223–236. https://doi.org/10.1080/18128600608685661

    [7]       Minh, C. C., Sano, K., & Matsumoto, S. (2005). The Speed, Flow and Headway Analyses of Motorcycle Traffic. Journal of the Eastern Asia Society for Transportation Studies, 6, 1496–1508. https://doi.org/10.11175/easts.6.1496

    [8]       Nguyen, H., & Montgomery, F. (2007). Different Models of Saturation Flow in Traffic Dominated by Motorcycles. Journal of the Eastern Asia Society for Transportation Studies, 7, 2381–2395. https://doi.org/10.11175/easts.7.2381

    [9]       Pooja, R., Shahana, A., Asaithambi, G., & Ravi Shankar, A. (2018, January). An Approach for Estimation of Passenger Car Unit Values of Vehicles Based on Influence of Neighboring Vehicles. Transportation Research Board Annual Meeting, Washington D.C., USA.

  [10]     Prahara, E., Nataatmadja, A. D., & Harviani, L. (2018). Analysis of motorcycle unit (MCU) for motorcycle- dominated traffic with effective space approach (case study: Jalan Raya Lenteng Agung Barat dan Jalan Teuku Nyak Arief). IOP Conference Series: Earth and Environmental Science, 195, 012014. https://doi.org/10.1088/1755-1315/195/1/012014

  [11]     Sai Kiran, M., & Verma, A. (2016). Review of Studies on Mixed Traffic Flow: Perspective of Developing Economies. Transportation in Developing Economies, 2(1), 5. https://doi.org/10.1007/s40890-016-0010-0

  [12]     Srikanth, S. (2019). Space Occupancy Method for Estimation of PCUs of Vehicles at Different Speed and Flow Ranges on Urban Road. SAMRIDDHI : A Journal of Physical Sciences, Engineering and Technology, 11(02), 77–84. https://doi.org/10.18090/samriddhi.v11i02.1

  [13]     The Indian Road Congress. (1990). Guidelines for Capacity of Urban Roads in Plain Areas, IRC: 106-1990. IRC: 106-1990.

  [14]     Transportation Research Board. (1965). Highway Capacity Manual, Special Report, 87.