DP-FEDAW: FEDERATED LEARNING WITH DIFFERENTIAL PRIVACY IN NON-IID DATA

 

Qingjie Tan ¹, Bin Wang ²,  Hongfeng Yu ¹, Shuhui Wu ¹, Yaguan Qian ¹, Yuanhong Tao ¹

 

¹ School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, Zhejiang, China

² Network and Information Security Laboratory of Hangzhou Hikvision, Digital Technology Co., Ltd., Hangzhou 310051, Zhejiang, China

 

1. INTRODUCTION

In recent years, with the explosive development of technologies such as the Internet of Things, cloud computing, and artificial intelligence, an unprecedented amount of data has been generated Zhang et al. (2018). This massive data contains incalculable knowledge and commercial value and has become an essential strategic resource that has received close attention from academia, industry, and governments worldwide. However, while utilizing this emerging data strategy resource, data privacy and security issues have also arisen Ping et al. (2017). Privacy and security have become core factors affecting data analysis and processing Xie et al. (2020). To address this problem, governments and organizations have issued a series of laws and regulations to protect data privacy and security. For example, the European Union's General Data Protection Regulation (GDPR) Tikkinen-Piri et al. (2018), enacted in 2018, stipulates that data collection and storage must be carried out with the consent of consumers, and China's Data Security Law, implemented in 2021, regulates data processing activities to protect data security and personal information Zhou et al. (2021). Therefore, how to fully tap the value of massive data resources while ensuring data security and complying with laws and regulations has become one of the significant challenges for current data analysis and processing.

To cope with the problems mentioned earlier, scholars have actively explored new privacy protection mechanisms and technologies to ensure data sharing and high-value development and utilization while protecting data privacy and security. Thus, Google proposed Federated Learning in 2017 Chen et al. (2020), a distributed machine learning method with privacy protection that can train learning models collaboratively using data from different users without transmitting data, thus efficiently utilizing the maximum value of data from all parties Konen et al. (2016). Federated Learning has attracted much attention since it was first proposed Zhang et al. (2021). Currently, Federated Learning has been applied in various hot areas, such as healthcare Kaissis et al. (2020), 6G Letaief et al. (2021), autonomous driving cars Pokhrel and Choi (2020), and traffic flow prediction Liu et al. (2020).

Although Federated Learning has dramatically improved the privacy and security of machine learning models and related processes, there are better solutions. The information leakage risk during the exchange of model parameters will require the combination of Federated Learning and other privacy protection technologies, such as differential privacy Wu et al. (2022), monophonic encryption Ma et al. (2022), secure multiparty computation Byrd and Polychroniadou (2020), Etc. Among them, differential privacy is a significant privacy and security protection technology that can further reduce the risk of any participant sharing and updating privacy data based on other data owners while maintaining the excellent performance of the learning model Dwork and Roth (2013). The Conference on Neural Information Processing Systems, the Artificial Intelligence Promotion Association Conference, the International Joint Conference on Artificial Intelligence, and other important international conferences on artificial intelligence have held discussions on Federated Learning and Differential Privacy Dinur and Nissim (2003). Therefore, research on Federated Learning with differential privacy is worthy of exploration. Specifically, in practical application scenarios, one of the critical characteristics of data processed by Federated Learning is the heterogeneity, which means that user data have significant differences in source, data volume, types, and acquired features.

On the other hand, the fast development of information technologies causes a massive amount of data, usually Non-IID. More and more proposed solutions to handle the Non-IID date in FL exist. Various recent works Zhang et al. (2022), Tian et al. (2022), Yu et al. (2022), You et al. (2023) have revealed that the biased classifier is the main cause leading to poor performance of the global model. Therefore, studying Federated Learning with differential privacy for heterogeneous data is essential.

 

2. Preliminaries  

2.1. Federated learning

As an emerging distributed machine learning scenario, Federated Learning enables multiple users to jointly train a machine learning model with the help of one or more central servers. In the Federated Learning scenario, the training data used for model learning is distributed across user devices. A more optimal distributed machine learning model is trained through iterative global aggregation and updates. During the model learning process, each participating user downloads the model parameters from the central server and performs local training based on their local datasets. After completion, the updated model parameters are uploaded to the central server. Throughout the learning process, end-users do not transfer their raw datasets, and the central server can only obtain the model training parameters of each user. The basic flow chart of Federated Learning is shown in Figure 1.

Figure 1

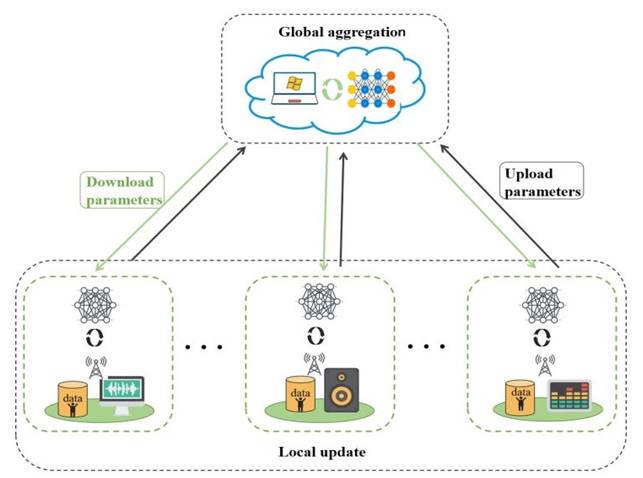
Figure 1 Schematic Diagram of the Federal Learning Process

 

Suppose that there are  users participating in the federated learning process, each user k has a local data set, and the size of the data set is, where,  is the data point i of user k, and is the label corresponding to the data point i of user k. The user communicates with the central server to facilitate training the model by minimizing the loss function , and the optimization problem of federated learning can be written as:

                                              

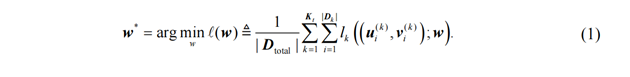
Where is the parameter vector;  is the total dataset involved in training.

 

2.2. Federated averaging algorithm

The federated averaging algorithm (FedAvg) Mcmahan et al. (2017) is currently the mainstream federated optimization method, which has achieved empirical success in heterogeneous data environments and provides a common starting point for solving the above problems. However, convergence problems still need to be faster and easier to adjust or even deviate from the optimal solution.

The main idea of the FedAvg algorithm is to randomly sample a subset of end users during the training process. The local users who participate in the training independently run a certain number of stochastic gradient descent steps to train the local data to obtain the local model, and transmit it to the central server. After receiving the model, the server aggregates the local model by means of averaging, and then updates the global model, and finally obtains a final model after multiple rounds of iterations. This algorithm can effectively reduce the risk of privacy leakage caused by the direct aggregation of raw data in traditional machine learning. At the same time, the algorithm can be applied to data reconstruction in Non-independent and identically distributed data, thereby ensuring data availability.

Assuming that  users participate in the federated learning process, each user has training data points and model weights obtained from local training in iteration t. Among them, the updated model parameters in the FedAvg algorithm are summarized as shown in formula (2):

 

                                                                                              

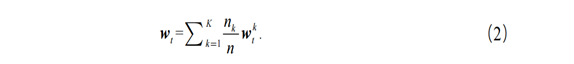
Where  refers to the global model weight update of the federated learning process;  refers to the total number of data points owned by all users.

 

2.3. Differential privacy

2.3.1.  The definition of differential privacy

Differential privacy can ensure that the influence of a single sample, on the whole, is always below a certain threshold when outputting information so that the attacker cannot analyze the situation of a single sample from the output change. Furthermore, the sum of privacy parameters in the Gaussian mechanism can quantify this degree of influence. The definition of differential privacy is shown in formula (3):

Assuming that the random algorithm  is for any two adjacent data sets  and  with a difference of one element, the set of all possible outputs for algorithm  is:

 

                                                                                           

 

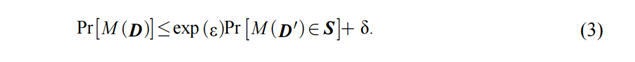
Then the algorithm  is said to be -differentially privacy.

where is the privacy budget; is the slack factor, which refers to the probability that privacy protection is not allowed, and the general value needs to be less than the reciprocal of the number of data sets; the privacy budget refers to the degree of privacy protection required by the user.

 

2.3.2.  Gaussian Mechanism

The realization process of differential privacy introduces randomness into the data by adding noise. Due to the impact of randomness, when we query data, it will prevent privacy leakage to a large extent and ensure that the accuracy of the query will not be too low. Therefore, we add Gaussian noise to the parameters produced by training in a federated learning environment to achieve differential privacy protection.

Definition of Gaussian mechanism: For the differential privacy function M defined above, if it satisfies the definition of formula (4):

 

                                                                              (4)

 

Where  is the output of the data set  in the real situation;  represents the global sensitivity of the function , and its possible output is the maximum distance obtained from the two norms of the adjacent database on the same function. The relevant definitions of 、  and  satisfy the following conditions:

 

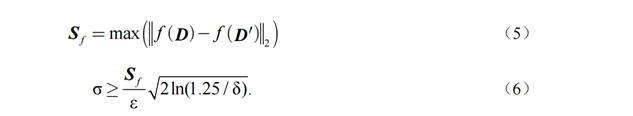
Then the function is said to be -differentially privacy. From this it can be observed that the noise level is directly proportional to the global sensitivity and inversely proportional to the privacy budget. That is, the greater the global sensitivity, the greater the injected noise, and the better the privacy protection effect.

 

3. Algorithm for Non-IID data

3.1. The effects of the Non-IID data

In the federated learning scenario, due to the Non-IID characteristics of the local data sets of each user participating in the training, there may be large differences between the local and global models. Even the gradient of some local models is opposite to that of the global model, so there is drift in the local model. In other words, the updated local model is biased towards the optimal local value and away from the optimal global value state Karimireddy et al. (2019), Li et al. (2022). Suppose these local models are uploaded to the PS for aggregation. In that case, the accuracy of the global model will be affected, and a large amount of network bandwidth will be occupied, which will affect the communication efficiency of model transmission.

Figure 2

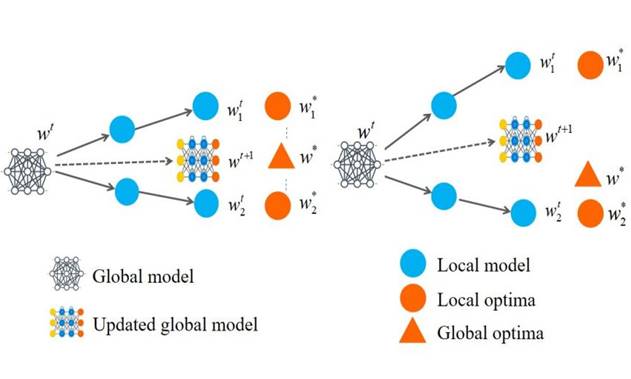
Figure 2 The FedAvg Problem in IID and Non-IID Data

 

Figure 2 shows the FedAvg problem in IID and Non-IID scenarios. Under the IID setting, the optimal global value is close to the optimal local value, and that is, the averaged global model tends to the optimal global value. In the Non-IID setting, because the optimal global value is far from the optimal local value, the averaged global model is also far from the optimal global state. Therefore, it is particularly important to study how to design an effective FL algorithm in Non-IID settings.

 

3.2. Mearements of the difference of two Non-IID data    

Based on impact of Non-IID data, we propose to use cosine similarity to measure the degree of Non-independent and identical distribution between different user data sets. This method mainly addresses the problem of poor federated learning performance caused by common user data Non-independent and identical distribution. Cosine similarity is to measure the difference between two vectors by measuring the cosine value of the angle between the inner product space of two vectors. The value range of cosine is that when the cosine value tends to 1, it means that the angle between the two vectors is closer to 0, and the direction of the vectors is getting closer at this time, which means that the two vectors are very similar. Let P and Q be the sample vectors of two users, and the calculation formula of cosine similarity is:

                                                                          

 

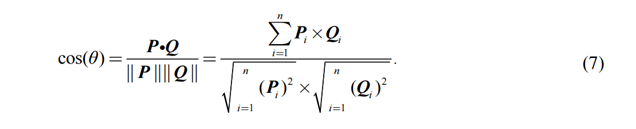
Where the numerator represents the vector inner product of P and Q; the denominator represents the product of the moduli of vectors P and Q.

In the iteration t, the label probability distribution of the local data set and the standard balanced data label probability distribution  are respectively obtained, and then the similarity degree is obtained by cosine similarity calculation according to the two types of distributions:

 

                                                                                                            (8)

 

3.3. Federated weighted average algorithm with differential privacy 

In order to avoid the leakage of user data caused by the leakage of model parameter information, we propose a federated weighted average algorithm with differential privacy (DP-FedAW). This algorithm adds noise to the model parameter information during model iteration, thereby perturbing the data, and the attacker also Almost no useful information can be obtained from it. Algorithm 1 shows the DP-FedAW proposed in this paper.

In order to protect the user's data information, the algorithm designs a differential privacy mechanism based on Gaussian noise. According to the requirements of privacy protection, noise parameters and privacy budget in differential privacy will be determined. Users can accurately calculate the privacy loss generated during each iteration training process through the combination theorem. When performing local updates, each user calculates the local gradient based on the global gradient sent by the central server and the local dataset, and adds Gaussian noise to perturb the gradient parameters that need to be uploaded. Finally, the server aggregates the model parameters and updates them, and broadcasts to the next The end user who participates in the training round. The process of adding noise is shown in equation (9):

 

Where the noise  follows a Gaussian distribution with an expectation of 0 and a variance of .

 

 

 

 

 

 

 

Algorithm 1

Algorithm 1 DP-FedAW

Input:is the number of users; is the local batch size；is the local training frequency of the model； is the model learning rate； is the probability distribution of balanced data labels

 

The aggregation method in the traditional federal average algorithm only depends on the amount of data held by each participating user to determine the weight coefficient. But when the user data is not independent and identically distributed, the model generated by this algorithm will cause certain errors. Therefore, we consider weighting according to the results of cosine similarity when aggregating models, which not only alleviates the difficulty of data training for Non-IID data, but also improves the efficiency of model training. Its core is to replace  in formula (2) with , and the model weight update parameters will also change with the number of iterations:

 

                                                                                                                                 

 

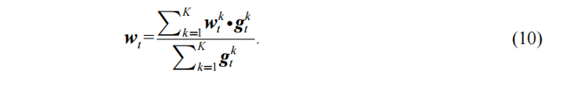
4. Analysis

In order to protect the data privacy of end users, federated learning algorithms generally have two strategies Li et al. (2019), namely 1) partial end user participation and 2) multiple local stochastic gradient descent method updates, so it can effectively improve the communication of distributed stochastic gradient descent efficiency. Therefore, we continued this strategy. Specifically, by selecting some end users to participate in the training, according to the federated average algorithm, only some users  are randomly activated to perform local updates and add Gaussian noise for disturbance, and then upload the latest parameters to the central server . If refers to the sampling process without replacement, then according to the Privacy Amplification Theorem Bassily et al. (2014), the differential privacy mechanism provides stronger privacy guarantees when performing model updates on random samples of the dataset obtained after sampling than on the full datasets.

The above results show that, especially when the data of each user is unbalanced, according to the effect of sampling, part of the end users participating in the training can reduce the number of communication rounds required to achieve a fixed accuracy rate.

Theorem 2 Assuming sampling probability is, if -DP is to be achieved in model training, the required noise level can be reduced

Proof: Because we assume that there is an equation for the sampling probability, and E refers to the number of updates performed locally by the end user in each communication round. Because

 

 

 

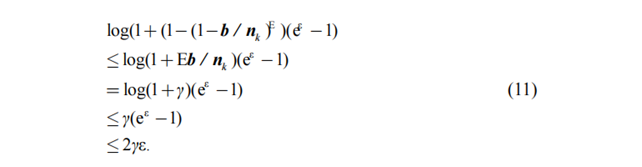
Then combined with the conclusion of Theorem 1, we can obtain that at least -DP is satisfied, and this result is substituted to obtain the noise level.

 

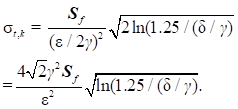                                                                                                       (12)

 

5. Experiments

5.1. Partition Dataset

This experiment uses the MNIST dataset, which mainly includes 70,000 handwritten digital grayscale image data, of which 60,000 images are used for training the model, and 10,000 images are used for testing the model. The size of all images is 28*28, and each image corresponds to a number label from 0-9.

In order to construct a Non-IID data set, we do some processing on the training set of the MNIST data set. Assuming that the total number of users participating in the training is , 60,000 images are evenly distributed to each user so that each user has 600 images. The proportion of users with Non-IID data is When it is 0, the corresponding users are in a normal equilibrium state, that is, the data set labels are evenly distributed. When it is 1, the corresponding user data sets are in a Non-IID state, that is, the data set label distribution There is a long-tail distribution. The specific processing method is shown in Figure 3 below:

Figure 3

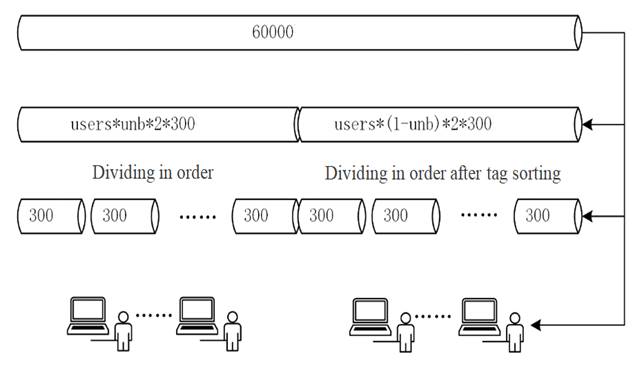
Figure 3 Non-IID Data Division

 

Through the construction method of IID data and Non-IID data, 60,000 images are divided to construct 200 data blocks with a size of 300 so that each user can obtain 2 data blocks. This construction method conforms to the IID data Case. Sort 60,000 images according to the image tags, and divide and construct 200 data blocks with a size of 300 according to the tags so that each user can get 2 data blocks. This construction method conforms to the situation of Non-IID data. Among them, after the data block is divided, it is allocated to the user using the random library in Numpy, and the same random seed is used for the same data set division results so that the results of each division are consistent and convenient for experiment development and analysis.

 

5.2. Experimental Setup

In terms of the model, a deep neural network is used to update the user's local model in federated learning, and Pytorch is selected as the framework. Stochastic gradient descent (SGD) is used as the optimization algorithm. The number of local training iterations is set to 10, the local batch size is set to 10, and the learning rate is set to 0.01. In federated learning, for experimental comparison and performance considerations, the number of communications between the central server and each end user is set to 10, the total number of end users is 100, and the ratio of participating in federated learning is set to 0.1. There are 10 end users in one communication Participate in training. In the comparison experiment, in order to investigate the performance difference between the DP-FedAvg algorithm Geyer et al. (2017) and the DP-FedAW algorithm, the size is set to 0.8. The framework for achieving differential privacy adopts the Opacus framework, which can be used to train PyTorch models with differential privacy, adding noise to the gradient in the iteration of the deep learning model instead of modifying the data directly and achieving differential privacy without accessing user data.

 

5.3. Two algorithms for two scenes

Figure 4 shows the model effects of the two algorithms in two types of scenarios with adding noise, that is, the comparison of training loss and classification accuracy between the DP-FedAvg algorithm and DP-FedAW in different situations.

Figure 4

 

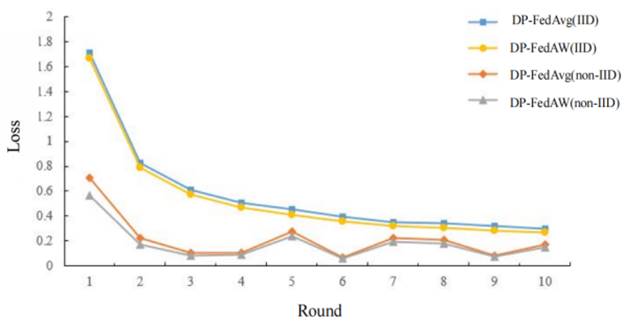
Figure 4 Scene Comparison Between DP-FedAvg and DP-FedAW Algorithms

 

The above test results show that in the 10 communications between the central server and each user, the two algorithms have achieved different training effects in the two types of data sets. Specifically: in the case of standard balanced data, the DP-FedAvg algorithm and DP-FedAW algorithms are well iterated, and as the number of communications increases, the model training loss can gradually decrease. In the case of Non-IID data, the iterative effects of the FedAvg algorithm and the DP-FedAW algorithm are not excellent. By comparing the standard balanced data, it can be seen that there is a phenomeNon of over-fitting.

 

5.4. Two algorithms for two different Non-IID distributions 

In order to judge the impact of the degree of data Non-IID on the two algorithms, it shows that the DP-FedAW algorithm has better robustness for Non-IID data, so keep the other parameters unchanged, and set the data Non-IID parameter varies from 10% to 100%.

Figure 5

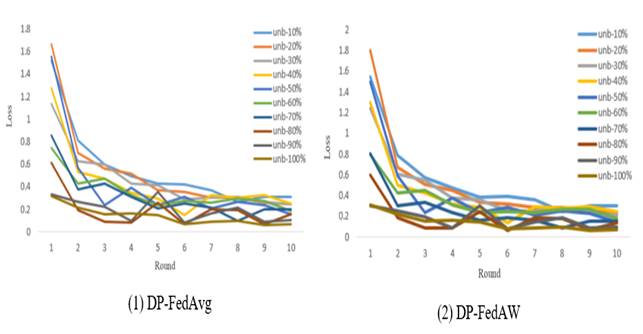
Figure 5 Comparison of training loss between two algorithms under different Non-IID states

In the 10 communication times between the central server and each end user, as shown in Figure 5, the training loss of the DP-FedAvg algorithm and the DP-FedAW algorithm changes with the number of communication times. It can be seen that the DP-FedAW algorithm can be compared with the DP-FedAvg algorithm. Good convergence, but equally prone to getting stuck in local optima.

Table 1

Table 1 Comparison of Accuracy of Two Algorithms Under Different Equilibrium Conditions
unb	Acc on DP-FedAvg	Acc on DP-FedAW
10%	96.6	96.8
20%	96.4	96.9
30%	96.3	96.8
40%	96.3	96.9
50%	95.7	96.1
60%	95.4	96.0
70%	93.9	96.2
80%	90.7	94.4
90%	90.6	94.4
100%	82.7	82.9

 

Comparing the model accuracy of the two algorithms under different degrees of Non-IID data and adjusting the parameter, the test results are shown in Table 1. At the same time, the model accuracy rate of the DP-FedAW algorithm is higher than that of the federated average algorithm under the setting of Non-IID of 10 sets of data. The experimental results of the two algorithms have the biggest difference of 3.85% when the disequilibrium state is 90%.

 

5.5. The effects of DP on the accuracy of model

To demonstrate the impact of privacy budget in differential privacy parameters on model accuracy when adding noise during training, we compared the DP-FedAW algorithm proposed in this paper with the FedAW algorithm without privacy on the MNIST dataset. Set the privacy budget to values ranging from 0.1 to 10.0, totaling 5 values.

Figure 6

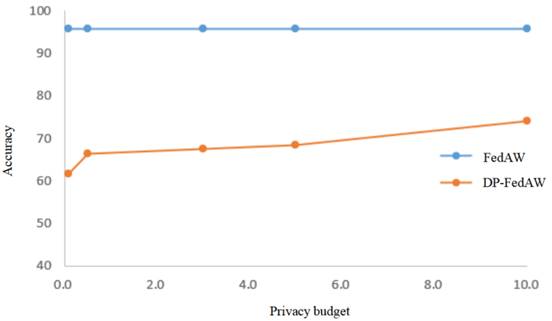
Figure 6 Privacy Budget Impact

As shown in Figure 6, with the increase of privacy budget, the accuracy of the model increases, gradually tending towards a situation without noise. The results show that the higher the privacy protection required by users, the smaller the privacy budget parameters need to be set, but this can also lead to a decrease in model performance. Therefore, it is necessary to find a suitable privacy budget parameter that can ensure the performance of the model while ensuring user privacy and security.

In order to analyze the effectiveness of federated learning algorithms with differential privacy constraints, Table 2 shows the comparison of classification accuracy between two classic federated learning algorithms with differential privacy and the DP-FedAW algorithm proposed in this paper in different data scenarios. We hope that the DP-FedAW algorithm can achieve higher accuracy in Non IID data scenarios compared to other algorithms.

Table 2

Table 2 Comparison of Accuracy of Different Algorithms in Different Scenarios
	Users	Acc on DP-FedAvg Geyer et al. (2017)	Acc on DP-FL Huang et al. (2020)	Acc on DP-FedAW
IID data	100	96.41%	94.20%	96.48%
Non-IID data	100	90.03%	93.90%	94.02%

 

From Table 2, we can see that the accuracy of the DP-FedAW algorithm is higher than that of DP-FedAvg and DP-FL in both IID and Non IID data scenarios. Meanwhile, the accuracy of the DP-FedAW algorithm in Non IID data scenarios is almost the same as that of the DP-FL algorithm in IID data scenarios. This verifies the effectiveness of the DP-FedAW algorithm for heterogeneous data scenarios.

 

6. Conclusion

In practical scenarios, data heterogeneity often leads to the slow convergence of the global model of federated learning and even the challenge of leaking model parameters. To solve this problem, we propose a federated weighted average algorithm with differential privacy, which quantifies the Non-IID data sets of different users by calculating the cosine similarity between each user's local data set and the IID data set. On this basis, the aggregation weight of each user is adjusted, which effectively alleviates the model convergence problem caused by the difference of Non-IID data in the training process. Then, a privacy-preserving federated weighted average algorithm is designed to ensure that the model parameters satisfy differential privacy. In the privacy protection stage of the local model, noise that satisfies the Gaussian distribution is added. The differential privacy technology is used to provide local privacy protection to obtain a more secure aggregation model that can guarantee good utility. Through theoretical analysis, we prove that the algorithm effectively guarantees the privacy and security of learning and training while simultaneously speeding up the convergence of the model. Experiments on public datasets show that the algorithm can converge faster than the federated averaging algorithm. In addition, with the increase of the privacy budget, the accuracy of the model gradually tends to the situation without adding noise under the condition of ensuring the model's safety.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Bassily, R., Smith, A., & Thakurta, A. (2014). Private Empirical Risk Minimization: Efficient Algorithms and Tight Error Bounds 55th Annual Symposium on Foundations of Computer Science, IEEE Publications, 464. https://doi.org/10.1109/FOCS.2014.56

Byrd, D., & Polychroniadou, A. (2020). Differentially Private Secure Multi-Party Computation for Federated Learning in Financial Applications. Proceedings of the First ACM International Conference on AI in Finance, 1. https://doi.org/10.1145/3383455.3422562

Chen, B., Cheng, X., Zhang, J. L. et al. (2020). A Survey of Federal Learning Security and Privacy Protection. Journal of Nanjing University of Aeronautics and Astronautics, 52(5), 10.

Dinur, I., & Nissim, K. (2003). Revealing Information While Preserving Privacy. Proceedings of the Twenty-Second ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, 207. https://doi.org/10.1145/773153.773173

 Dwork, C., & Roth, A. (2013). The Algorithmic Foundations of Differential Privacy. Foundations and Trends® in Theoretical Computer Science, 9(3-4), 211-407. https://doi.org/10.1561/0400000042

Geyer, R., Klein, T., & Nabi, M. (2017). Differentially Private Federated Learning: A Client Level Perspective. 

Huang, X., Ding, Y., Jiang, Z. L., Qi, S., Wang, X., & Liao, Q. (2020). DP-FL: A Novel Differentially Private Federated Learning Framework for the Unbalanced Data. World Wide Web, 23(4), 2529-2545. https://doi.org/10.1007/s11280-020-00780-4

Kaissis, G. A., Makowski, M. R., Rückert, D., & Braren, R. F. (2020). Secure, Privacy Preserving and Federated Machine Learning in Medical Imaging. Nature Machine Intelligence, 2(6), 305-311. https://doi.org/10.1038/s42256-020-0186-1

Karimireddy, S. P., Kale, S., Mohri, M. et al. (2019). SCAFFOLD: Stochastic Controlled Averaging for On-Device Federated Learning.

Konen, J., Mcmahan, H. B., Yu, F. X. et al. (2016). Federated Learning: Strategies for Improving Communication Efficiency.   

Letaief, K. B., Shi, Y., Lu, J., & Lu, J. (2021). Edge Artificial Intelligence for 6G: Vision, Enabling Technologies, and Applications. IEEE Journal on Selected Areas in Communications, 40(1), 5-36. https://doi.org/10.1109/JSAC.2021.3126076

Li, Q., Diao, Y., Chen, Q. et al. (2022). Federated Learning on Non-IIND Data Silos: An Experimental Study 38th International Conference on Data Engineering (ICDE), IEEE Publications, 965. https://doi.org/10.1109/ICDE53745.2022.00077

Li, X., Huang, K., Yang, W. et al. (2019). On the Convergence of FedAvg on Non-IIND Data.  

Liu, Y., Yu, J. J. Q., Kang, J., Niyato, D., & Zhang, S. (2020). Privacy-Preserving Traffic Flow Prediction: A Federated Learning Approach. IEEE Internet of Things Journal, 7(8), 7751-7763. https://doi.org/10.1109/JIOT.2020.2991401

Ma, J., Naas, S. A., Sigg, S., & Lyu, X. (2022). Privacy-Preserving Federated Learning Based on Multi-Key Homomorphic Encryption. International Journal of Intelligent Systems, 37(9), 5880-5901. https://doi.org/10.1002/int.22818

Mcmahan, H., Moore, E., Ramage, D. et al. (2017). Communication-Efficient Learning of Deep Networks from Decentralized Data. Artificial Intelligence and Statistics. PMLR, 1273.

Ping, L., Li, J., Huang, Z. et al. (2017). Multi-Key Privacy Preserving Deep Learning in Cloud Computing. Future Generation Computer Systems, 74(7), 76. https://doi.org/10.1016/j.future.2017.02.006

Pokhrel, S. R., & Choi, J. (2020). Federated Learning with Blockchain for Autonomous Vehicles: Analysis and Design Challenges. IEEE Transactions on Communications, 68(8), 4734-4746. https://doi.org/10.1109/TCOMM.2020.2990686

Tian, P., Liao, W., Yu, W., & Blasch, E. (2022). WSCC: A Weight-Similarity-Based Client Clustering Approach for Non-IID Federated Learning. IEEE Internet of Things Journal, 9(20), 20243-20256. https://doi.org/10.1109/JIOT.2022.3175149

Tikkinen-Piri, C., Rohunen, A., & Markkula, J. (2018). EU General Data Protection Regulation: Changes and Implications for Personal Data Collecting Companies. Computer Law and Security Review, 34(1), 134-153. https://doi.org/10.1016/j.clsr.2017.05.015

Wu, X., Zhang, Y., Shi, M., Li, P., Li, R., & Xiong, N. N. (2022). An Adaptive Federated Learning Scheme with Differential Privacy Preserving. Future Generation Computer Systems, 127(6), 362-372. https://doi.org/10.1016/j.future.2021.09.015

Xie, Y., Wang, H., Yu, B., & Zhang, C. (2020). Secure Collaborative Few-Shot Learning. Knowledge-Based Systems, 203(7553), 106157. https://doi.org/10.1016/j.knosys.2020.106157

You, X., Liu, X., Jiang, N., Cai, J., & Ying, Z. (2023). Reschedule Gradients: Temporal Non-IID Resilient Federated Learning. IEEE Internet of Things Journal, 10(1), 747-762. https://doi.org/10.1109/JIOT.2022.3203233

Yu, M., Zheng, Z., Li, Q., Wu, F., & Zheng, J. (2022). A Comprehensive Study on Personalized Federated Learning with Non-IID Data. IEEE intl. Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), 40.  https://doi.org/10.1109/ISPA-BDCloud-SocialCom-SustainCom57177.2022.00013

Zhang, C., Xie, Y., Bai, H., Yu, B., Li, W., & Gao, Y. (2021). A Survey on Federated Learning. Knowledge-Based Systems, 216(1), 106775. https://doi.org/10.1016/j.knosys.2021.106775

Zhang, L., Shen, L., Ding, L., Tao, D., & Duan, L. (2022). Fine-Tuning Global Model Via Data-Free Knowledge Distillation for non-IID Federated Learning, 10164-10173. IEEE Publications. https://doi.org/10.1109/CVPR52688.2022.00993

Zhang, Q., Yang, L. T., Chen, Z., & Li, P. (2018). A Survey on Deep Learning For Big Data. Information Fusion, 42(5), 146-157. https://doi.org/10.1016/j.inffus.2017.10.006

Zhou, C. X., Sun, Y., Wang, D. G. et al. (2021). A Survey of Federated Learning Research. Chinese Journal of Network and Information Security, 7(5), 77.