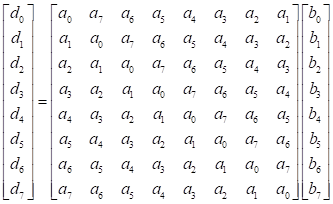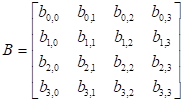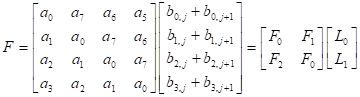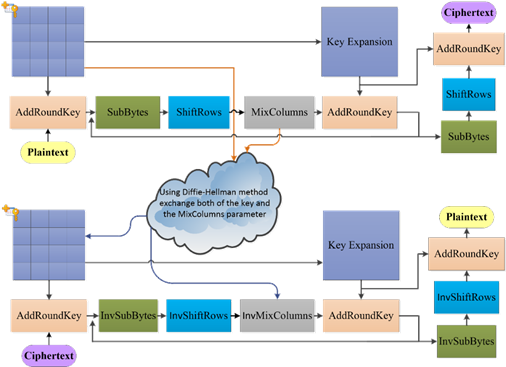
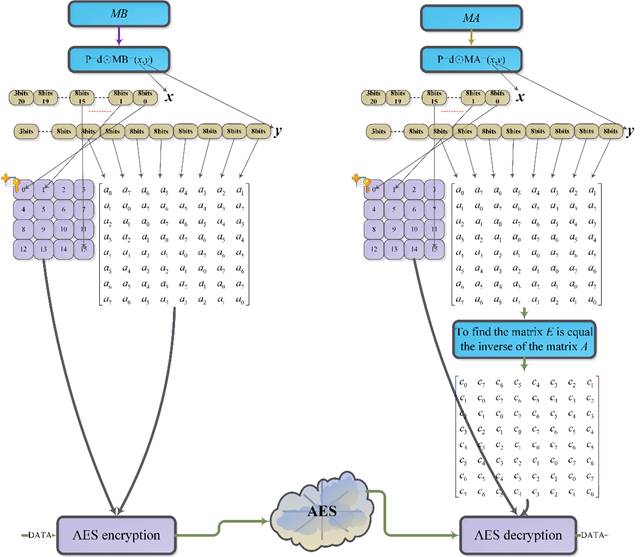
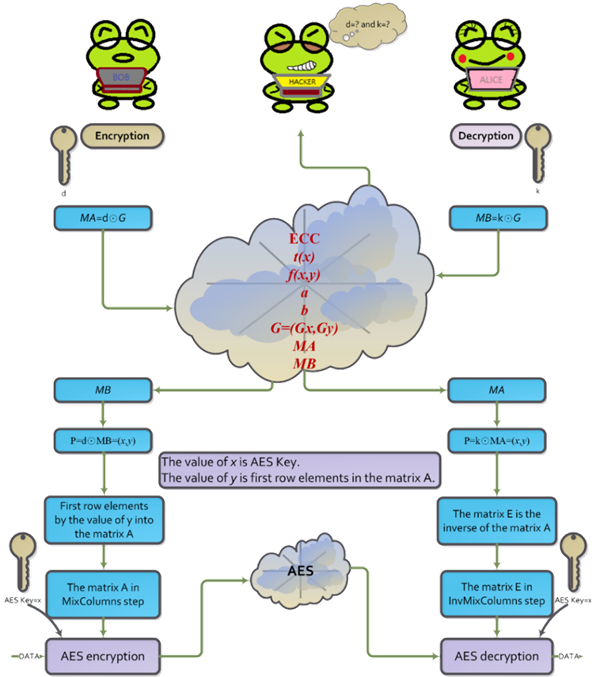
(Daemen and Rijmen (1999); National Institute of Standards and Technology (NIST) (2001). Matrix operations utilize different methods of multiplication in the finite field (Chen and Huang (2020); Stepanov and Rose (2015); Wang et al. (1983);  Mahboob and Ikram (2006); Reed and Chen (1999)). Thus, the methods are used in the encryption and decryption, such as the Rijndael method and the Twofish method (Schneier et al. (1998). In addition, due to attacks (Biryukov  Khovratovich (2009) is a computation complexity 2 method by a known-key distinguishing attack in AES-128. Therefore, that can use the diversty of the matrix to enhance security (Wang et al. (2020). In this paper, the idea is using the diversity 8´8 circulant matrix, it has large branch number for diffusion more than 4´4 involutory matrix. Therefore, we propose an enhancement security method for AES encryption/decryption transformations with the Elliptic Curve Diffie–Hellman key exchange (ECDH) using elliptic curve in ANSI X9.62. Therefore, the AES key and first rows of the matrix can use ECDH method for exchanging both. The method will be more difficult for attacking which is to avoid the key by pre-computing the possible output to attacks. We propose method can be designed for a circuit (Selimis et al. (2006); Jing et al. (2007); Wang et al. (2016); Maximov (2019); Langenberg et al. (2020); Yang and Chien (2020), the circuit can decrease logic gates to use. Finally, using 8´8 circulant matrix is running for AES key of 128 bits on Intel(R) Core(TM) i7-8700 CPU. The reducing encryption time is above 79% faster than the 8´8 involutory matrix multiplication. Finally, the paper is in combining diversity AES and ECDH methods for security enhancement approaches to protect against new threats. The flowchart is as shown in Figure 1.

 

Figure 1 New AES for encryption and decryption

 

2.    PRELIMINARIES

2.1. FINITE FIELD MULTIPLICATION:

Let  and  be two polynomials of degree m-1 in GF(2^m), where . The addition is given:

 

 

 

(1)

 

Where  is a polynomial. The equation (1) written in the program by C language form as:

 

unsigned char a, b, c;

c=a ^ b;

 

In this paper, the symbol of  is an XOR bitwise operation that is an instruction of the CPU. It is not required an extra function to programming. The multiplication modulo an irreducible polynomial given as,

 

(2)

 

Where an irreducible polynomial is . In (2), using the Russian Peasant multiplication, the powers of two in the decomposition of the multiplicand that it on the left shift to discarding any remainder. The multiplication is writing a programming code in the C language as follows:

 

Russian Peasant multiplication

unsigned char GFM(unsigned char a, unsigned char b){ unsigned char c = 0; for (int j = 0; j < 8; j++){ if (b & 1) c ^= a; if (a & 0x80) a = (a << 1) ^ 0x11b; else a <<= 1; b >>= 1; } return c;}

 

In (2), using Horner rule, the multiplication is writing a programming in the C language as follows:

 

Horner’s rule

unsigned char t[4]; unsigned char BT[4]; unsigned char GFM(unsigned char a, unsigned char b){ unsigned char c; t[0] = 0; t[1] = 0x1b; t[2] = 0x36; t[3] = 0x2d; BT[0] = 0; BT[1] = b; BT[2] = (b << 1); if (b & 0x80) BT[2] = (b << 1) ^ 0x1b; BT[3] = BT[2] ^ b; c= BT[(a >> 6) & 0x3]; c=(c << 2) ^ t[c >> 6] ^ BT[(a >> 4) & 0x3]; c=(c << 2) ^ t[c >> 6] ^ BT[(a >> 2) & 0x3]; c=(c << 2) ^ t[c >> 6] ^ BT[a & 0x3]; return c; }

 

 

2.2. MATRIX MULTIPLICATION

 

Let  and  be the polynomial equation of degree m-1 in GF(2^m), where ∈ GF(2^m).  is a polynomial in GF(2⁸). The polynomial a(x) and b(x) are multiplication as below:

 

(3)

 

Where the polynomial c(x) is remainder. Its degree is m-1 in GF(2^m) as follows:

 

.

(4)

 

The d_i for  is shown as below:

 

 

It can be rewritten as from as follows:

 

.

(5)

 

Where the d_i for , it can be represented a matrix from (6).

 

(6)

 

 

 

 

 

 

 

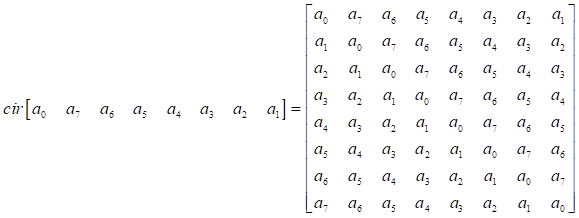
The 2´2 circulant matrix is defined as , where 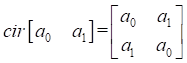. The 8´8 circulant matrix is defined  as follows:

 

 

2.3. CIRCULANT MATRIX MULTIPLICATION BY 4´4

In Scheme 1, it computes 4´4 circulant matrix method, there are three items  which can be precomputed in the program, so that the method only used 5 multiplications and 15 additions, namely (5M, 15A). if  is equal to one, Scheme 1 see in ( Wang et al. (2020) authors, 2020) is shown as follows:

 

Scheme 1. (5M, 15A);

{ }

 

 

 

 

 

 

 

 

3.    MATRIX MULTIPLICATION IN AES MIXCOLUMNS OVER GF(2⁸)

 

The polynomial product  is accomplished with the polynomial  in AES standard, where , . In MixColumns encoding, the matrix A is the diffusion circulant matrix and matrix B is data.

 

,

(7)

 

it needs running four times in AES MixColumns steps. The , the j-th column is encrypted by  matrix, where  that is given,

 

.

 

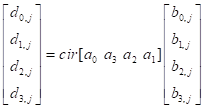In this paper, we use the polynomial product  is accomplished with the polynomial , where , . If we use 8´8 matrix in AES MixColumns transformations, the data matrix is rewritten from as 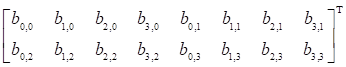 matrix for 8´8 circulant matrix multiplication. In this case, it is only running two times for a MixColumns step. Let matrix B be the data for encryption, the data matrix B is given in , the j-th column data is encrypted by  8´8 matrix, where .

The circulant matrix A multiply matrix B is from as follows:

 

 

 

 

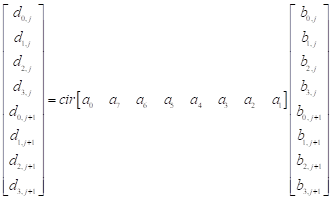
3.1. DECREASING MULTIPLICATIONS FOR 8´8 CIRCULANT MATRIX

The 8´8 matrix multiplication is defined as follows:

 

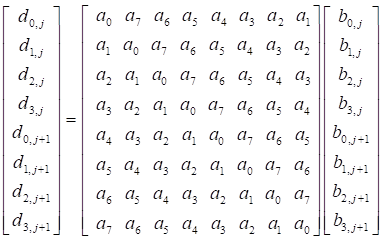
                                                            where , , , , ,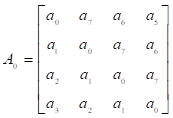

.

 

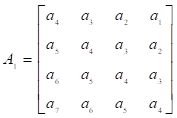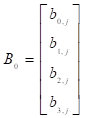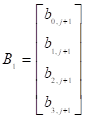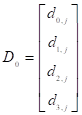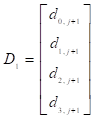Using the two-points convolution method instead of 8´8 matrix multiplication, it can be shown a  matrix and multiply the matrix .

 

(8)

 

3.2. REDUCING MULTIPLICATIONS BY MULTIPLY 2

According to (8),  and . In the finite field addition property is , where , then the property can be also the same using in the matrix from additions. For example, if  adds , it is equal to  because  is zero and  is also the same property. Therefore, we rewrite in the equation (8) into the equation (9).

 

.

(9)

 

Where  and .

 

 

Let…., ,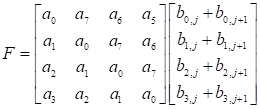

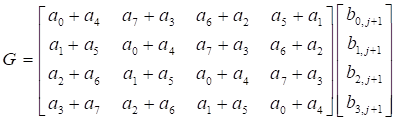and .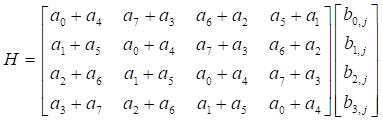

 

Both the matrix G and the matrix H have circulant matrix property, so it uses Scheme 1 to compute 4´4 matrix multiplication. However, the 4´4 matrix F, there is not circulant matrix property, then we can use other method to solve this problem. Now, the matrix product F can be written for the properties of addition over GF(2^m).

 

,

(10)

 

Where , , , , 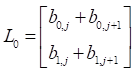and .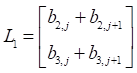

 

Adding two entries of  and  are into matrix product F as follows:

 

(11)

 

In (11), the matrix product  can be also further simplified by properties of addition over GF(2^m).

 

 

 

 

Where , , , , and . Both the matrix f₁ and the matrix f₂ are the same by two points convolution procedure.

, and

 

.

 

The matrix f₀, matrix f_1, and the matrix f₂ are into equation (11).

 

 

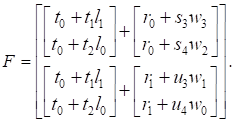
Where ,,,, , , , , , , , , , , ,, and . The matrix F rewritten function is called MF( ).

 

Scheme 2. (9M, 19A);

, ,, ,, , , { , , , , , , , , }

 

 

 

 

 

 

Finally, the matrix D can be from as follows:

 

 

Therefore, Scheme 2, (i.e., MF()), for matrix F is 9M & 19A, Scheme 1, (i.e., M4()) for the matrix G is 5M & 15A, Scheme 1 for the matrix H is 5M & 15A. Finally, the entries of the matrix D is given by calling MF() and M4(), and then there are four value returned from function MF() and M4() to addition, respectively, where the symbol of  represent 4 additions. For example，let

 

.

.

.

 

 

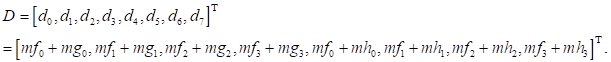
That meaning require 8 additions, the total number of the matrix D operation is 19M and 57A.

 

3.3. THE INVERSE OF 8´8 MATRIX FOR AES INVMIXCOLUMNS

The others method, the inversion matrix is given by mathematics, Gaussian elimination is a method for finding inverse of the matrix A. It consists of a sequence of operations performed on the corresponding coefficients of the matrix A. However, the speed is slower than using the adjoint of the matrix A because Gaussian elimination method, there are many divisors for computing the matrix A and the matrix I, that’s why we choose to adjoint method in finding the inverse of the matrix. The matrix  has a property , then where . How to be more efficient getting its inverse matrix  using analytic solution as follows:

 

.

 

The transpose of the matrix A of cofactors, it is the same an adjugate matrix, can be an efficient method to compute the inverse matrix. The inverse matrix is divided det(A) equal to  because  

 

 

 

 

Therefore, if the matrix A is circulant matrix, the matrix  is also circulant matrix. This meaning, we can only use the first rows to obtain entries cofactors as follows:

 

 

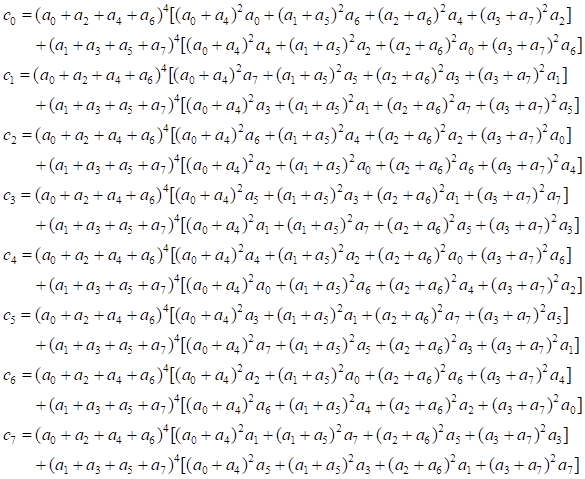
Therefore, the first rows of matrix  also has  as shown below:

 

 

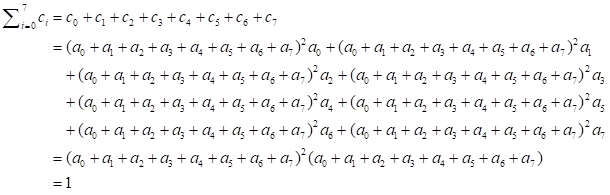
The sum of the coefficients of the polynomial  is one, means . For example   has  property, the inverse of matrix A is . Now, the procedure can use searching the sum of the coefficients of the polynomial A(x) that has the property  and the coefficients of the polynomial A(x)^-1 also has the sum . There are many a pair of entries to find the coefficients of the polynomial A for AES MixColumns transformation and the coefficients of the polynomial A^-1 for InvMixColumns transformation. There are some a pair of entries as shown in Table 1.

 

Table 1 The sum of the coefficients of the polynomial A(x) is one.
Items
1	b6	0d	1f	93	22	9b	d1	5e		28	d3	69	f3	64	68	7f	13
2	02	8d	97	49	10	ff	1b	a4		d8	df	cb	e1	28	9b	a5	3a
3	9f	70	d4	1c	c0	a0	91	d7		4f	04	da	51	fd	67	72	29
4	15	97	19	b6	90	d6	7a	10		38	b1	06	a6	69	6c	b1	9c
5	6f	65	6d	f6	ac	33	83	8c		8b	a9	25	14	be	35	3d	a4
6	33	a2	ba	2b	9b	13	ef	66		c2	45	26	3e	1b	93	02	14
7	7f	fe	9b	6c	70	88	71	fe		eb	93	4b	64	b4	f8	f1	eb
8	19	86	c0	1d	6c	10	7f	40		d8	f1	ab	b3	c4	7a	7d	f3
9	4d	78	5f	2b	4c	81	e6	6b		96	f6	f1	6b	99	ad	46	89
10	30	30	74	f8	6c	f0	e1	f0		85	08	52	ba	ec	8c	f2	f6
11	c5	80	57	b2	f1	b8	a7	4f		a4	a2	9b	bb	63	49	98	95
12	40	5d	3c	94	36	67	87	62		48	33	8d	97	b0	e6	b8	8e
13	ae	58	19	a6	a7	9f	28	58		09	b4	f7	5c	7c	39	ba	e8
14	78	94	bb	d5	19	92	36	3e		5a	7d	96	2e	87	cb	a7	75
15	2e	8b	be	13	0a	32	93	a2		0b	c7	a9	1b	59	48	f2	9c
16	8d	99	f9	66	e1	a0	3a	f1		49	24	dc	0d	ac	36	96	b1
17	bc	f7	fc	d6	aa	ec	82	a4		0a	23	39	dd	fd	5f	a6	c8
18	2e	23	53	b4	9a	76	7f	78		f2	f9	e0	2f	7f	55	f5	1a
19	ea	13	5c	30	89	1e	e8	eb		a2	1b	9d	c9	9d	74	75	70
20	e7	3a	61	33	c6	8c	b9	7d		a3	d7	72	51	a2	47	8a	39

 

4.    RESULT AND DISCUSSIONS

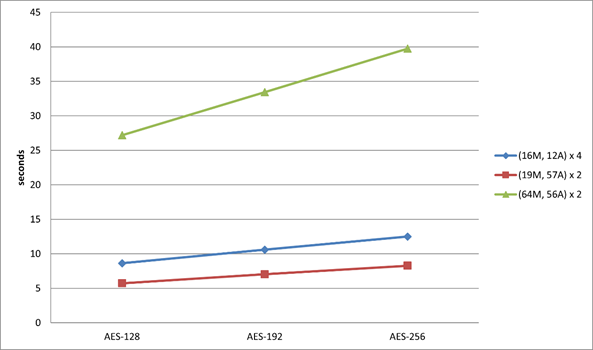
Using the multiplication based on several algorithms in GF(2^m) and the new matrix multiplication method are for evaluating encryption and decryption procedure running 1,000,000 times state with different AES key lengths, where the state is 4´4 bytes for encryption and decryption. The keys with lengths 128, 192, 256 bits run cipher and InvCipher average execution time as shown in Table 2 and Figure 2. Using 8´8 circulant matrix (19M, 57A) in AES MixColumns steps, the key of sizes 128, 192, 256 bits can be faster than using 4´4 involutory matrix operation ~33.5%, ~33.7%, and ~33.9%, respectively. In MixColumns steps, using 8´8 circulant matrix (19M, 57A)´2 operation faster than 4´4 involutory matrix (16M, 12A)´4 in AES MixColumns steps. In the AES key 128bits with the circulant matrix (19M, 57A)´2 is above 79% faster than 8´8 involutory matrix (64M, 56A)´2. Finally, the Figure 2, the symbol “M” represents the multiplications and the symbol “A” represents the additions.

 

 

 

 

 

 

 

Table 2 The execution time for three different key lengths (128, 192, or 256 bits)
MixColumns/IvnMixColumns	AES-128	AES-192	AES-256
(16M, 12A) ´ 4	8.62	10.6	12.49
(19M, 57A) ´ 2	5.73	7.02	8.26
(64M, 56A) ´ 2	27.19	33.44	39.75

 

Figure 2 AES execution time with the different key lengths

 

In the paper, using Elliptic-curve Diffie–Hellman (ECDH) method exchanges both AES key and first row elements of the MixColumns matrix to allows two parties, as shown in Figure 3. This security is elliptic curve points using addition to derive the same a point x and y as AES key and first row elements of the MixColumns matrix, respectively. The values x and y of the point can be used to encrypt consecutive communications using a symmetric key. However, the value of y is the first row of elements in MixColumns matrix that must be computed first row element into inverse circulant matrix for the MixColumns steps, and then decryption. ECDH is a key exchanging protocol that admits two parties.

 

Figure 3 Using ECDH exchange AES key and MixColumns matrix

 

For example, how to share key got it. If Alice wants to establish a shared key with Bob, the only channel available for them may be eavesdropped on by a hacker. Publicly, the parameters; that is, the binary case in GF(2^m) is (m, t(x), a, b, G, n, h), where t(x) is irreducible polynomial, the value of a, b is the parameter of the elliptic-cure, G is the point of the elliptic-curve. The only information is about the Alice public key. So, no person can include Alice to determine Alice's private key, unless that party can solve the elliptic curve discrete logarithm problem. Bob's private key is also secure. No person can compute Alice or Bob the shared secret unless that person can solve the elliptic curve Diffie–Hellman problem. How to choose ECC the size of m in GF(2^m) for exchanging AES key and first row elements of the MixColumns matrix, if we use AES key size of 128 bits length, ECDH method using in elliptic curve of the points in GF(2¹⁶³) is meaning x and y of the coordinate with 163 bits. In other words, The elliptic curve of the points is in GF(2²³³) that can be used for AES key size of 163 bits and 192 bits. The AES key size is 256 bits that need the elliptic curve of the points in GF(2²⁸³). So, GF(2²⁸³) can be used in AES key sizes of 128 bits, 192bits, and 256 bits. The elements at first row of the MixColumns matrix (i.e., first row elements of the matrix A) are 4 bytes or 32 bits that the meaningful y in the point P = (x, y) is enough bits to store first row elements of the MixColumns matrix as shown in Figure 4.

 

Figure 4 The ECC m=163 bits for AES key and MixColumns matrix

 

5.    CONCLUSIONS AND RECOMMENDATIONS

In summary, it is demonstrated herein that the computational complexity matrix multiplication over GF(2⁸) can be minimized by 2-point cyclic convolution property. In comparison for the 88 circulant matrix running on Intel(R) Core (TM) i7-8700 CPU with more reduced ~34% time than 4´4 involutory matrix in different key size for MixColumns operation. If the sum of coefficients of the polynomial is not one, then there are more a pair of matrices that can use for enhancing scarcity system. However, we only found in some a pair of matrices by the sum of coefficients of the polynomial is one (i.e., ), which the number of a pair of matrices is enough for security communication in IoT (Internal of Things) system. The proposed method in Figure 1 can be an extended procedure of AES with more variations in the MixColumns matrix for enhanced security of data transmissions. In the future, the method may also be used for designing VLSI circuits to save the number of logic gates in diverse MixColumns and InvMixColumns transformations. In future work, the method would be used 16´16 circulant matrix in GF(2^m) for computing AES MixColumns and InvMixColumns operation.

 

ACKNOWLEDGEMENTS

This study was supported in part by Taiwan’s Ministry of Science and Technology MOST 110-2813-C-214-019-E and MOST 110-2221-E-214-007.

 

 

REFERENCES

A. Biryukov, D. Khovratovich (2009), “Related-Key cryptanalysis of the full AES-192 and AES-256,” In: Matsui, M. (ed.) ASIACRYPT 2009 LNCS, 5912, pp. 1-18 https://eprint.iacr.org/2009/317.pdf. Retrieved from https://doi.org/10.1007/978-3-642-10366-7_1

A. Mahboob, N. Ikram (2006), “Lookup table based multiplication technique for GF(2m) with cryptographic significance,” IEE Proc. Commun, vol. 52, no. 6, pp. 965-974. Retrieved from  https://doi.org/10.1049/ip-com:20050022

A. Maximov (2019), “AES MixColumn with 92 XOR gates,” Cryptology ePrint Archive, Report 2019/833, Retrieved from https://eprint.iacr.org/2019/833 , Jul.

A. Stepanov, D. Rose (2015), From mathematics to generic programming. Pearson Education, New York, 3st edn, pp. 9.

B. Langenberg, H. Pham, and R. Steinwandt (2020), "Reducing the Cost of Implementing the Advanced Encryption Standard as a Quantum Circuit," in IEEE Trans. on Quantum Engineering, vol. 1, no. 2500112, pp. 1-12. Retrieved from https://doi.org/10.1109/TQE.2020.2965697

B. Schneier, J. Kelsey, D. Whiting, D. Wagner, and C. Hall (1998), “Twofish: a 128-Bit block cipher,” Available NIST's AES homepage, Retrieved from https://www.schneier.com/academic/paperfiles/paper-twofish-paper.pdf.

C. C. Wang, T. K. Truong, H. M. Shao, L. J. Deutsch, J. K. Omura, and I. S. Reed (1983), “VLSI architectures for computing multiplications and inverses in GF(2m),” TDA Progress Report, pp. 42-75. Retrieved from https://doi.org/10.1109/tc.1985.1676616

C. H. Yang and Y. S. Chien (2020), “FPGA Implementation and Design of a Hybrid Chaos-AES Color Image Encryption Algorithm,” Symmetry, vol. 12, no. 2, 187, pp. 1-17. Retrieved from https://doi.org/10.3390/sym12020189

D. Augot, M. Finiasz (2013), “Exhaustive search for small dimension recursive MDS diffusion layers for block ciphers and hash functions,” IEEE Int. Conf. on Information Theory, Turkey, pp 1551-1555, Jul. Retrieved from https://doi.org/10.1109/ISIT.2013.6620487

D. Yin, Y. Gao (2017), “A new construction of lightweight MDS matrices,” IEEE Int. Conf. on Computer and Communication, pp. 2560-2563. Retrieved from https://doi.org/10.1109/CompComm.2017.8322997

F. J. MacWilliams, N. J. Sloane (1978), The theory of error-correcting codes: North-Holland, 1nd edn.

G. N. Selimis, A. P. Fournaris, and O. Koufopavlou (2006), “Applying low power techniques in AES MixColumn/InvMixColumn transformations,” IEEE Int. Conf, Electronics, Circuits and Systems ICECS’06, France, pp. 10-13, Dec. Retrieved from https://doi.org/10.1109/ICECS.2006.379628

I. S. Reed, T. K. Truong (1978), “A fast computation of complex convolution using a hybrid transform,” DNS Progress Report, pp. 42-46. Retrieved from https://doi.org/10.1109/TASSP.1978.1163150

I. S. Reed, X. Chen (1999), Error-control coding for data networks, Kluwer Academic Publishers, Boston. Retrieved from https://doi.org/10.1007/978-1-4615-5005-1

J. Daemen, V. Rijmen (1999), AES proposal: Rijndael, document version 2. Retrieved from https://doi.org/10.1109/LCOMM.2004.833807

J. Lacan and J. Fimes (2004), “Systematic MDS erasure codes based on vandermonde matrices,” IEEE Trans. Commun. Lett., vol. 8, no. 9, pp. 570-572. Retrieved from https://doi.org/10.1109/LCOMM.2004.833807

J. Nakahara Jr, E. Abrahao (2009), “A New involutory MDS matrix for the AES,” International Journal of Network Security, vol.9, no.2, pp.109–116.  Retrieved from  https://d1wqtxts1xzle7.cloudfront.net/30902835/ijns-2009-v9-n2-p109-116.pdf?1362934357=&response-content-disposition=inline%3B+filename%3DA_New_Involutory_MDS_Matrix_for_the_AES.pdf&Expires=1632550400&Signature=fMBdhnUJNMZwPR2Vty-P-3dLJ9EKIaeLeFVGoFXz4oo1fFu1Y71GuCtdiYnzUBL4Byh63sc~Y0LUYFXShECE5c6~s3m8zYWmZVwepIX1czUfQbIK~2Ei5crxbZqRxxISHNMAeCcLEh0Y0yQvA5iXVEb0D9-wphLT46rurVt3MDtgxtx-YKWzVAiP1bSzpBtaFa84OZJc8dRsE60uontP90CwrfMmeqmLaqrvkB1GSie45RPP5x398x6RVy73Y~B4TSlu2mCUmXq1fOdwIue~ykBbjjopEa1iH9PdFgV6TCRYdFSaeIZaHF1-o-9J817X4LJERCSUTUY8MGALlWTYKw__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA

Jeng-Jung Wang, Yan-Haw Chen, Guan-Hsiung Liaw, Jack Chang, Cheng-Chih Lee (2020), "Efficient schemes with diverse of a pair of circulant matrices for AES MixColumns-InvMixcolumns transformation," Communications_of_the_CCISA, vol. 26, no. 2, pp. 1-20. Retrieved from https://cccisa.ccisa.org.tw/article/view/2314

M. H. Jing, Z. H. Chen, J. H. Chen, and Y. H. Chen (2007), “System for high-speed and diversified AES using FPGA,” Microprocessors and Microsystems, vol. 31, pp. 94–102, Mar. Retrieved from https://doi.org/10.1016/j.micpro.2006.02.018

National Institute of Standards and Technology (NIST) (2001) “Advanced Encryption Standard (AES),” PUBS FIPS 197, Nov.

P. Junod, S. Vaudenay (2004), Perfect diffusion primitives for block ciphers. building efficient MDS Matrices. Federalede Lausanne, Switzerland. Retrieved from https://doi.org/10.1007/978-3-540-30564-4_6

S. Winograd (1978), “On computing the discrete Fourier transform,” Mathematics of computation, vol. 32, no.141, pp. 175-199. Retrieved from https://doi.org/10.1090/S0025-5718-1978-0468306-4

T. Luong (2016), “Constructing effectively MDS and recursive MDS matrices by Reed-Solomon codes,” Journal of Science and Technology on Information security, pp. 10-15. Retrieved from http://tailieu.antoanthongtin.vn/Files/files/site-2/files/MDS%20matric.pdf

Y. H. Chen, C. H. Huang (2020), "Efficient operations in large finite field for elliptic curve cryptographic,” International Journal of Engineering Technologies and Management Research, vol. 7, no. 6, pp. 141-151. Retrieved from https://doi.org/10.29121/ijetmr.v7.i6.2020.712

Y. Wang, L. Ni, C. H. Chang, and H. Yu (2016), “DW-AES: A Domain-Wall Nanowire-Based AES for high throughput and energy-efficient data encryption in Non-Volatile memory,” IEEE T INF FOREN SEC, vol. 11, no. 11, pp. 2426-2440. Retrieved from https://doi.org/10.1109/TIFS.2016.2576903