FL has also made improvements in the privacy and security of machine learning models because the server process aggregates only local parameters from each user and the server doesn’t know anything about user raw data. In fact, the practical results of FL are very effective in protecting sensitive users’ data. It is very attractive to many real word applications, such as hospitals, financial institutions, and governments. On the other hand, new computing paradigms of FL have also attracted the attention of adversaries with malicious intent. Consequently, they may have effects on the model update, or they may make suggestions that include a user’s privacy. Thus, FL is not the best solution in protecting privacy [Yang et al. (2019)].

Due to the importance of privacy and security of data processing, there is growing amount of literature, which has attempted to provide solutions [McMahan et al. (2016), Aledhari et al. (2020)]. Privacy preserving and security mechanisms have been considered to incorporate with FL across the entire system. Differential privacy (DP) is one of these main mechanisms [Dwork (2008), Dwork (2006)]. For DP, some randomized mechanisms, such as Laplace mechanism, Gaussian mechanism and exponential mechanisms, have been used to add random noises to the output of query so that the adversary can’t differentiate between two distinct inputs [Zhu et al. (2020), Erlingsson et al. (2014)].

FL with DP is the cutting-edge of research on privacy protection from theoretical aspect as well as from a practical perspective [Ding et al. (2017), Liu et al. (2021)]. Even though, integrating DP with FL is not an effective enough way for solving all privacy problems. Thus, the shuffle model has been proposed. In [Cheu et al. (2019)], the first protocol of real summation with shuffle model have been presented, which showed that O () messages sending by k users via shuffle achieved O (1) mean square error (MSE) in central model. The technique of the shuffle model was proposed to deal with the problem between privacy in center model and accuracy in local model.

The framework of DP-FL with shuffle model consists of users, shuffle and analyzer [Balle et al. (2019), Meehan et al. (2021), Erlingsson et al. (2019), Bittau  et al. (2017)]. In this framework, users train their model by using their own data set, using local randomization to implement DP. Afterwards, each user sends the local noised parameters as a message to the shuffle, and the shuffle perturbs users’ messages by using randomly permutation π then send these messages to analyzer. Finally, the analyzer aggregates all messages from shuffle for analysis and creates the global model. Briefly, the untrusted analyzer receives m messages from users’ entity via shuffle functionality. This model has been proved that it has the ability to overcome the limitations on accuracy of local algorithms, while protecting several of their appropriate attributes. In order to gain a comprehensive understanding of the state-of-the art DP-FL with shuffle model, we conduct this survey. The main contributions of this survey are

·         The first comprehensive survey on the current research on DP-FL with shuffle model.

·         A taxonomy of solution published to 2021 for shuffle model in DP-FL.

·         Some promising research directions for the future work.

 

This survey is structured as follows. In Section 2, we introduce all the necessary notations throughout the paper. Section 3, we summarizes the recent published papers on DP-FL with shuffle model. Section 4 we outline the shuffle model and his role in boosting privacy in FL with achieving accuracy and privacy amplification. Lastly, we conclude out paper in Section 6.

 

2.     Backgrounds

In this section, we shall introduce the necessary notations that needed through our paper. At first, the common notations have been presented in the following table.

 

Table 1 The common notations though out the paper
Notations	Explanation	Notations	Explanation
D, D′	two neighboring datasets	X	Sample space
Y	Output space	N	Size of Dataset
ℳ	Algorithm mechanism	D	Dimension of sample space
K	Number of users	W	vector weight of gradient descent
T	Communication round	C	Clipping parameter
Η	Hyper parameter (learning rate)	L(.)	Laplace mechanism
ɛ	Privacy budget	π	Random permutation in shuffle
Δ	Possibility of Violating ɛ -DP	F(·)	Sensitivity function
Α	The order of Renyi divergence between two distributions P and Q	N	The number of examples in training process
µ(x)	Data distribution	εμ	Privacy budget for BDP
δμ	Possibility of Violating εμ	N(0,σ2)	Gaussian mechanism
|| ƒ ||	Norm of function ƒ	⁓	Approximately equal

 

2.1. Federated learning

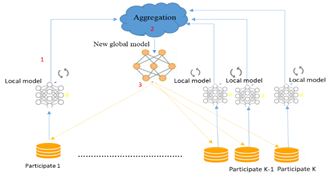
FL is an improved type of DML in which, the training process is distributed among many users and the server has the role of coordinating everything by aggregating gradients from participants [Kairouz et al. (2021)] as shown in Figure 1.

Figure 1 Federated learning training process

 

From the above Figure 1, training process of FL usually takes three steps [Yang et al. (2019)]. In the first step, all participates train their data from the local model then upload it to the server (the aggregator). In the second step, the aggregator collects all participators’ local parameters from local models to produce efficient global model. In the third step, the aggregator distributes the global model parameters to all users in order to retrain their data on it. The training process performs iterations until achieving the optimal global model that demonstrates high accuracy in users’ local model. Notably, in FL the users upload the local parameters rather than the local data, providing certain security for sensitive information about users.

 

2.2. Differential privacy

The concept of DP has been long among the privacy protection mechanism. DP is a verifiable privacy notion proposed by Dwork [Dwork (2006)], which is a mechanism to protect sensitive data from leakage by adding some noise on users’ data and returning statistically indistinguishable results. It means that DP guarantees that any adversary doesn’t have high probability of assuming whether a participated client is in the input by monitoring the output. If we have two datasets D, D’ ⸦ ⅅ satisfy D ⸦ D’ and D’=|D|+1, then D, D’ are said that they are two adjacent datasets and written as D⁓D’. The definition is as following.

Definition 1. (ε-DP [Dwork (2006)]) A randomized mechanism ℳ: D→R gives ε-DP if for any adjacent datasets D, D’ ⸦ⅅ, and all output S ⊆ R, where R is a Range ℳ

 

Pr[ℳ (D) ∊ S] ≤ e^є Pr [ℳ(D’) ∊ S ],                                          (1)

 

where є is the privacy budget that control the privacy level of ℳ.

For a lesser є the probability distributions of output results over ℳ on D and D’ are very similar and it is hard to differentiate both datasets. The relaxation version of є-DP is (є, δ)- DP, in which δ was added when we do not have pure privacy to detect violate ɛ. The notation of (є, δ) DP is as follows.

Definition 2. ((є, δ)-DP [18]) A randomized mechanism ℳ: D→R gives ((є, δ)-DP if for any neighboring datasets D, D’ ⸦ D, and all output S ⊆ R, R is Range (ℳ).

 

   Pr [ℳ (D) ∊ S] ≤ e^є Pr [ℳ (D’) ∊ S] +δ,                             (2)

 

Where S refers to the output domain of the algorithm ℳ.

If δ = 0, the mechanism ℳ provides є-DP by its stringent definition. If δ > 0, (ɛ, δ)-DP offers liberty to interrupt strict є-DP for some low probability events. In brief, DP can be realized by adding an affordable amount of noise into the output results of the query function. This amount of noise will effect on the balance between privacy and accuracy in the overall model. Namely, large amount of noise will make the dataset unusable and too small noise is not sufficient for DP collateral. The noise amount can be identified by computing the sensitivity.

Definition 3. (Sensitivity [Awan and Slavkovi'c. (2018)]) For an enquiry function ƒ, the sensitivity of ƒ is set as

 

 ∆ƒ= Max_D,D’ ||f(D) – f(D’)||_l,                                                  (3)

 

Where || . ||_l is l norm.

Note that, there are three standard techniques that are used to realize (є-δ) DP for all systems, Laplace mechanism [Phan et al. (2017)], Gaussian mechanism [Liu (2019)], and exponential mechanism. For numerical results, Laplace mechanism and the Gaussian mechanism are broadly used to realize DP. For non-numeric results, the exponential technique is used.

 

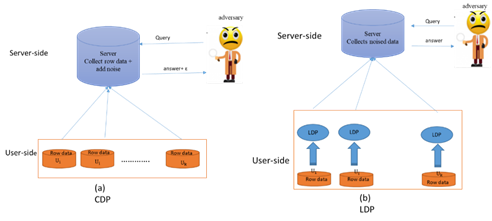
2.2.1.   Central deferential privacy (CDP)

Based on DP definition, CDP is regarded as a disaggregated technique of DP [McMahan et al. (2018)], which provides secrecy for the overall system by adding random noise to the aggregated output in the central part after collecting all the data from participating users. Consequently, the server will access to the user’s true data. It provides a good accuracy but rely on trusted analyzer. 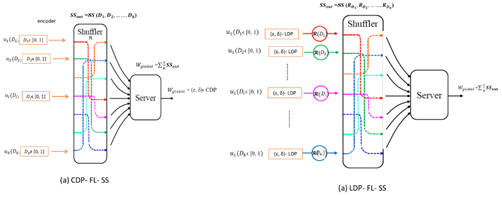The greatly difference between CDP and LDP is that CDP is a central privacy model with the supposition of a confidential analyzer where the users sent their data directly to server. Afterwards, the noise was added to query mechanisms (Figure 2 (a)). On the other hand, LDP is a local privacy model with no supposition on the analyzer and every client’s data is locally disturbed in the user-side before transferred to the analyzer.

 

2.2.2.   Local differential privacy (LDP)

LDP is a disaggregated modification of DP which permits each participator to perturbs his own data locally and transmits the disturbed data to the analyzer (Figure 2 (b)). Hence, the server will not transfer contact to the user real data, thus providing a robust privacy. In LDP, the input of perturbation mechanism is raw users’ data and the disturbed data is like as the mechanism output Geyer et al. (2020), Farhad. (2021), Zhao et al. (2020), Dwork (2011)]. The formal definition of (ɛ, δ) - LDP is similar with definition 2.

Figure 2 The framework of (a) CDP and (b) LDP.

 

2.3. Shuffle model

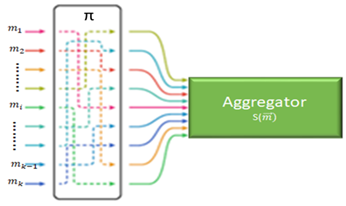
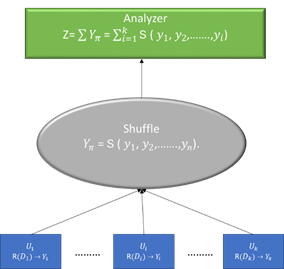
A shuffler (SS) is a randomized mechanism that hides all the notification about the positions of each user message by implementing a unified random permutation π of entries then returns the results after permutation (Figure 3) [Beimel et al. (2020)]. More formally, assume that we have M messages from k participators and each one has m_i ϵ M messages where m_i (1 ≤ i ≤ k) denotes to i user message. For the shuffler SS: m^k → m^k, the output shuffle will be SS_out(M) ₌ m_i^π . As far as privacy, shuffle model plays a great role in privacy amplification. Because SS can perturb input messages before sending it to aggregator. By this way, it hides the position of users’ messages from analyzer. Hence, the privacy of users data doesn’t depend on only adding (ɛ, δ)-DP for users’ data but also depend on the shuffle perturbation π. The communication model of SS is described as follows:

Definition 4. (Communication model in SS [Balle et al. (2019)]) Suppose that we have a vector of m messages from k users and every user sends its message to the shuffler. The protocol of SS communication model which represents distributed messages among k users is P = SS(m), where m= m₁, m₂, ……., m_k and SS is the shuffle functionality that choose a permutation π for users’ messages. The shuffle output is SS_out(m) = (m₁^π, m₂^π, …., m_k^π). The formal explanation of ЅЅ protocol is shown in Algorithm 1.

Figure 3 Shuffle channel

 

Algorithm 1 : The communication model with shuffle model Initialization: let K be the number of users, m be the users’ messages, and T be the communication round. Output: the global weight w While 1 ≤ i ≤ K # of users If 1 ≤ t ≤ T do 1)       All users train their model to generating K messages m= m1, m2,...., mk. Then, send the vector of messages m to ՏՏ 2)       ՏՏ receives m from users. 3)       ЅЅ permutes all messages by using random permutation π. 4)       ЅЅ output ЅЅoutput = (m1π, m2π, …., mkπ), then ЅЅ sends SSoutput to analyzer. 5)       the analyzer aggregates SSoutput to get the optimal model weight, w = 6)       t = t+1 Output: return w

 

3.     The applications of federated learning

To demonstrate the importance of FL, we present the applications of FL in this section. There is a huge amount studies on  applying FL in real life since the significance of FL has been recognized.

1)     FL in health care: Conventionally, healthcare records from scattered sites are progressed to a central database for analysis, which includes huge mount of data from each data source. In the past year, a huge number of changes has practiced due to the pandemic situation. The lack of resources in the healthcare industry was quite evident during this time. Therefore, the new way of transforming the healthcare data has been proposed in the healthcare industry. In [Liu et al. (2018)], a community-based FL algorithm has been recommended to expect mortality and hospital residence time. Electronic medical records are assembled into communities inside each hospital based on common medical sides. Each assemble learns and shares a particular ML model rather than the overall one mutual among all hospitals and hence patients. In [Huang et al. (2019)], the authors has proposed FL to predict hospitalizations during a target year for patients having heart disease using EHR’s data extent among numerous data sources. In [Li et al. (2019)], DP-FL technique has been considered to predict medical image for brain tumor segmentation to prevent any leakage of information. It suggests the cooperation of several organizations by sharing their locally computing models.

2)     FL in IoT system: FL aims to secure the data collecting through different mediums. Hence, FL can help to achieve personalization as well as enhance the performance of devices in IoT applications. In [Jiang et al. (2019), Ren et al. (2019)], the method is to use deep reinforcement learning to improve unloading results for IoT systems. The main idea is to consider proxy data is fewer related to the data kept on IoT machines. Consequently, IoT machines are responsible for the training models while edge nodes are for updating aggregation. The effectiveness of participating in IoT with FL has been demonstrated with edge computing when training deep reinforcement learning.

3)     FL in blockchain: Blockchain has been used recently to transfer money in Bitcoin without center server, where all users’ accounts are saved in public blockchain, then this public block is broadcasting to every part in the network. Each user is locally contributes to the overall blockchain by adding a new blocks in sequential order that provides an indelible and transparent record of transactions. The public can only see that someone has added a transaction with a quantity without knowing any sensitive information about depositor. FL framework is similar with blockchain framework in downloading global parameters for users to train their data, and then uploads it to server. According to [Nakamoto (2019), Sarfaraz et al. (2021)], the model contains a permission FL part and a block chain part, while the blockchain checks if a set of queries has been preceded or not. In addition, the multiparty data recovery process identifies to gain the outcomes of queries and then upload it to the aggregator instead of shearing the real information directly to the analyzer. The data consists of two types, useable data toward the requirements and reduced secret data of users.

4)     FL in recommendation system: Recommendation system requires data from users. Thus, it is very dangerous on privacy if users’ data is shared directly. FL acts as privacy-preserving system for recommendation systems in many cases, for example a virtual keyboard prediction in mobile devices [Hard et al. (2018)]. The familiar example on virtual key board is Google virtual keyboard (g-board) which need features prediction similar with autocorrection of spelling faults, next word prediction and offers communication features, such as, emoji, GIFs, and stickers [Yang et al. (2018), Ramaswamy et al. (2019)]. So it is necessary that g-board guarantees client privacy. Because the client may be type sensitive information like password. Hence, FL occupies a new view of federated recommender systems (Fed-Rec), which is an embodiment of FL on decentralized recommendation to save sensitive client information from leakage.

 

4.     Differential privacy in federated learning

We shall present the framework DP-FL in this section. FL has been designed to protect data privacy by being distributed learning systems that keep the data in its storage stores. FL allows training a massive amount of data privately due to its decentralized structure, which is adept meaningfully preserving users’ sensitive data from being visible to opponents. However, sensitive data can still be disclosed by exploring uploaded parameters from participators during the training process. One the other hand, as a mechanism to improve the security of data privacy, DP has been widely studied to make the model more secure and protect sensitive information of users.

There are two main models to implement DP with FL, which are local model and central models. For local differential privacy (LDP) model, each user trains its data and implements DP before uploading the parameter to untrusted server. In this model, all clients enjoy with high privacy but the server suffers from low utility due to the huge amount of noise that has been added to clients [Zhao et al. (2019)]. In central differential privacy (CDP) model, all users train their own data and upload the local parameters to trusted server without adding any noise, then the server aggregates the users’ parameters and adds DP for aggregated model [McMahan et al. (2018), Xixi et al. (2020)]. In this model, the server enjoys with high accuracy but the users suffer from low privacy due to trusted server.

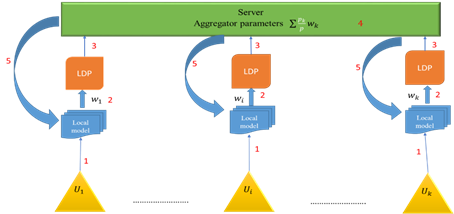
Here we give an example of FL-LDP. The framework of FL-LDP is shown in Figure 4 in details according to [Wei et al. (2020)]. The training process of LDP-FL usually takes the following five steps:

1)     The server distributes the initial weight w₀ to all users, then each user starts to train its data with the initial weight and get the optimum local model by using gradient descent method w_i^t = arg (min _wi f_i(w_i))+ (μ/2))|| w_i – w^t-1||² .

2)     Each user clips the local parameter from local model w_i^(t) = w_i^t / max (1, || (w_i^t / C)||).

3)     Each user adds DP mechanism for the local parameter by using Laplace mechanism before sending it to analyzer =w_i^t + lap(∆f/ε).

4)     The server aggregates the noised parameters from users w_g = .

5)     The aggregator broadcasts the global parameter w_g to k users for retraining their data on it.

Figure 4 Federated learning with local differential privacy

 

Algorithm 2 : FL with LDP Data: Let T be a communication round, w0 be  the initial weight, μ be hyper parameter, and ɛ and δ be privacy parameters. 1)       Initialization: t = 1 ;wi0  , ∀i 2)       While  0< t ≤ T do 3)       While ki ∈ {k1,, k2, . . . , kn} do      // k is number of users. 4)       wit = arg (minwi fi(wi))+ (μ/2))|| wi – wt-1||2 5)       wi(t) = wit / max (1, || wit / C||) 6)       =wit + lap(∆f/ε) is sensitivity function. 7)       wg = . 8)       for ki ∈ {k1,, k2, . . . , kn} do 9)       Test the aggregating parameter wg using local dataset minwi fi(wg) 10)   End 11)   t ← t + 1 Result: return wg.

 

5.     Differentially private federated learning with the shuffle model

Integrating DP with FL, it still not be a perfect solution. The recent studies suggest an intermediate model between users and the analyzer to eliminate the weaknesses points in both DP and LDP by reducing the gap between privacy and utility. This intermediate model called shuffle model. In practically, the shuffle model has achieved good results in privacy amplifications with higher accuracy than DP-FL system without shuffle model. In this survey, we shall discuss the influence of privacy on FL, starting from FL with DP to adding shuffle model in order to achieve a better balance between privacy and accuracy.

The framework of FL-DP in the shuffle model has attracted lots of attention recently. To see the advantages of the shuffle model toward DP-FL, it requires a thorough understanding DP-FL-SS.

 

5.1. The private multi-messages FL in a shuffle model

In this subsection, we shall introduce the private multi-message in a shuffle model [Balle et al. (2019)]. For the framework, please see the following Figure 5.

 

Figure 5 (a) Center differential privacy and (b) Local differential privacy with Shuffle model

 

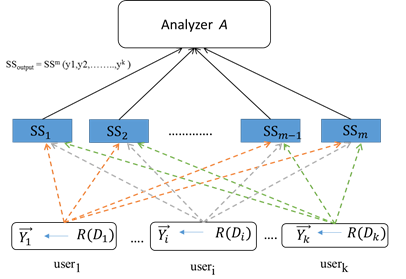
Both frame have their own pron and con. One approach is to apply secure multi-party computation to simulate central model algorithms while the other is to provide accuracy in local model. Both models include differential privacy with shuffle model (DP-SS). In [Bittau et al. (2017)], a special case of encoder shuffle analyze framework has been considered. At first, users perform a local randomized encode and then the users generalize the randomization messages. Then SS collects messages from users and randomly permutes it by a permutation π. Afterwards, the analyzer aggregates the users’ messages after shuffling. From analysis aspect, SS handles the problem of accuracy limitations on local algorithm with protective many of their necessary attributes under natural restrictions. In [Balcer and Cheu (2019), Ghazi et al (2020), Ghazi et al. (2020)], the overall protocol of DP-SS has been studied. This protocol contains three parts P = R, SS, A, where R: D →Y^k, SS: Y^k → SS_out, A: SS_out → O, R is local randomizer, D is dataset, Y is the output space after randomization, k is the number of users, SS is the shuffle, A is the analyzer of P which collects shuffled output and getting the optimal global model and O is the analyzer output. In DP-SS, users only need to trust that the shuffler acts as intended and sufficiently many of their peers follow the protocol.

Figure 6 DP-FL in the shuffle model

 

The mechanism that represents the overall protocol of the framework in Figure 6 starts from users’ data until gets final model from analyzer is P: D → O. The main implementation is as follow:

1)     Assume that we have k users, which has its own data D_i ϵ D, where i denoted to the number of users. Each one encodes his data D_iϵ [0, 1] and creating DP according to its dataset. For adjacent datasets D, D’, the encoder randomization is R: D→Y^k. If ever user transmits only one message every round, the output of this randomization is a vector of messages Y = y₁, y₂, ….., y_k = (R_D1, R_D2, …., R_Dk), which is the input for SS.

2)     The shuffle receives Y messages and then make a random permutation π for the messages vector. The output after the permutation is Y_π = SS (y₁, y₂, ….., y_k).

3)     The analyzer receives Y_π from shuffle and aggregates it to create the global model w_g=Σ(1/k)Y_π, then distributes the global model parameters to users via SS. As showed in last step, the randomization comes from both local randomizing from users side and permutation π from SS. Thus, the formula of the overall protocol P can be written as P = A, SS (R_D1, R_D2, …., R_Dk) . Let the mechanism be ℳ_R = ՏS (R_D1, R_D2, …., R_Dk). Then the overall protocol is P = A, ℳ_R, which is shown in Algorithm 3.

Definition 5 (SS towards DP-FL [Cheu et al. (2019)]) Let the mechanism ℳ_R = Տ, R^k detect the sight of the analyzer in an implementation of the protocol P, where R^k = (R_D1, R_D2, …., R_Dk) is local randomizer, and SS is the shuffle permutation. We can say that if the randomized mechanism ℳ_R gurantees (ε, δ)-DP if for every two adjacent datasets D, D’, for all output v ⊆ Range (ℳ_R), we have

                          

  Pr[ℳ_R (D) ∊ v] ≤ e^є Pr[ℳ_R (D’) ∊ v ] +δ                            (3)

 

Algorithm 3 : LDP - FL via shuffle model # Local Randomizer in user side Input: Let  D = (D1, D2, …, Dk) be users’ data sets, k be a number of users, yi be user output after adding LDP yi ϵ {0,1}, and w0 be server initial weight. 1)       While 1 ≤ i ≤ k do 2)       Analyzer distributes the initial weight (w0) to all users via shuffle 3)       For Di ϵ (D1, D2, …, Dk) 4)       Every user creates local update of initial weight Di = fi(w0) 5)       Encoding local updates by each user Di ϵ {0,1} 6)       (Di + C)/2C →Di*      # clipping parameters 7)       R(Di) = Di* + lap(∆f/ε)    # local randomization 8)       R(Di) → yi 9)       Return yi # Shuffle 10)   Y= (y1,y2 ,….,yk) 11)   Yπ = ՏS (y1,y2 ,….,yk). # Analyzer 12)   Z* = Σ(1/k)Yπ 13)   Normalize C(2Z* -1) → Z 14)   Return Z. Updates model.

 

5.2. The private multi messages FL via m parallel shuffle models

In this subsection, we shall introduce the private multi messages FL via m parallel shuffles models [Balle et al. (2020)]. In this type, m parallel shuffles have been introduced to receive multi messages from each user instead of using single shuffle, which further improves the accuracy and communication more than using single shuffle.

Suppose that there are k users. If each one randomizes its data set D_i, where R: D → Y^k, and all users send k randomized messages to m parallel shufflers, then each shuffle perturbs randomly k messages ЅЅ^m: Y^k → Y^k and the output is ЅЅ_output = ЅЅ^m (y₁,y₂,……..,y_k ). The analyzer receives km perturbed messages from m parallel shuffle A: (Y^k)^m →(ЅЅ)_output , then aggregates it to create the optimal global model. The framework of this technique explained in Figure 7 .

Definition 6. (The Communication model of multi messages in m parallel shuffles models [Balle et al. (2020)]): The protocol which presents this communication model of multi messages in m parallel shuffle is P = (R, A) if let D be the user dataset, where D = (D₁, D₂, ……, D_k). Each user i randomizes its own sensitive data by using local randomization to obtain vector of messages Y= (y₁, y₂,…….., y_k)= R(D_k). The users then send the vector of messages vector to independent parallel shuffles ЅЅⁱ: Y^k → Y^k, i ϵ [m] number of the  shufflers. Each shuffler perturbs randomly k messages that receive from users Yⁱ_π⁼ ЅЅⁱ (y₁ⁱ, y₂ⁱ,……, y_kⁱ). The analyzer then aggregates all parallel shufflers output results. In summary, the output of P(D) is given by P(D)= A, ЅЅ^m, R^m(D) = A(ЅЅ^m (y₁^m ,y₂^m,…,y_k^m)).

Figure 7 Privacy multi messages in m parallel shuffle

 

From the privacy aspect, the overall privacy of model has been divided to two parts, including privacy from randomization in users’ data, and the privacy from perturbation by using m shufflers. So the shuffle models play a great role in boosting privacy for users’ messages before uploading it to the analyzer. Therefore the total randomization comes from two aspects of DP view at users and permutation π from m shufflers. To prove the privacy, we will refer to the mechanism ϒ_R= ЅЅ^m (y₁^{m ,}y₂^m,………y_k^m) is the total randomization mechanism which captures the sight of the analyzer in an performance of the protocol. Note that we can rewrite the overall mechanism asℳ_p (D) = A, ϒ_R.

Definition 7 (DP-m shuffles [Balle et al. (2020)]): Assume that the mechanism ϒ_R = ЅЅ^m, R^m(D), is the analyzer view as an implementation of the protocol P(D). We can say that the mechanism ℳ_p (D) guarantees (ε, δ)-DP if for every two adjacent datasets D, D’, and all output S ⊆Range (ϒ_R),

 

          Pr[ϒ_R (D) ∊ S] ≤ e^є Pr[ϒ_R (D’) ∊ S ] +δ.                                             (4)

 

Note that, if m =1 means the total randomization ϒ_R= ЅЅ (y_1,y₂,………y_k), which is a single shuffle. According to [14], the resulting protocol after shuffling satisfies (ϵ, δ)-DP with ɛ= min (ɛ₀, 1) e^ɛ0, if the mechanism ϒ_R satisfies (ϵ₀-DP).

 

5.3. The accuracy in multi messages shuffle model(s)

In this section, we shall present the accuracy in multi messages shuffle model(s). To quantify the effect of this protocol in accuracy, we should measure the mean square error (MSE) at the worst case as the following definition.

Definition 8 (MSE in SS [Ghazi et al.  (2020)]): Let k be the number of users, which has real number data set D_i,  where D_i ϵ [0, 1]. If the protocol P of m messages in the shuffle model is quantified by a pair of algorithms P = (R, A), then the calculating the overall model accuracy in terms of MSE worst instance in each P is

             MSE (P) = Sup_{Di ϵ [0, 1]} E[(ℳ_p (D) -)²],                                    (5)

Where  is the real Summation and the prediction is finish the stochastic in the overall protocol ℳ_p (D).

For CDP, the Laplace mechanism guarantees (ε, δ)-DP in the case of real summation with MSE = O (1) and this is the optimal value. While LDP raises the tradeoff between accuracy and communication privacy by computing both in terms of the messages number per client and size of these messages. If the user send O (log(k/δ)), the MSE is O(1/ϵ²) in LDP model, which is much smaller than O(log(k/δ))² [Balle et al. (2020)].

 

5.4. The accuracy in multi messages shuffle model for binary summation

In this section we shall show how shuffle model solved the problem of binary summation which FL-LDP failed to solve it. The setting of this problem is that if we have k users, each one has dataset D_i, where i ϵ [k], and each one encodes his data D_iϵ [0, 1] bits. The purpose is to calculate the sum of bits in analyzer [Balle et al. (2019)].

To implement DP, the randomized response is the official local privacy for this problem. If D, D’ are neighboring datasets that differ in only one record. The encoder randomization is R(D)→y^k. Let user i send the message y_i. Due to subsampling and noise accumulation, the predictable value of summation y_i in the analyzer is = (1 - p) + k/p=2, where p is the probability of random response. The analyzer obtains an unbiased estimator as follows

        A_rr(Y) = (1/(1-p)) + kp/2),                                                    (6)

          E[A_rr(Y)] = (1/(1-p)) E[+ kp/2)]= .                       (7)

 

 

 

The local model view, LDP satisfy (ε, δ)-DP at P → 2/(e^ε + 1) with optimal error O ((1/ɛ)). It means the error increased when k increased [Meehan et al. (2021), 65].

According to [Cheu et al. (2019)], after adding shuffle model, the randomized response P_RR = (R_RR, A_RR) is a single-message protocol, where R_RR is the local randomization of users data and shuffle model R_RR = SՏ(Y)= SՏ (y₁, y₂, …, y_k) and A_RR is the analyzer that collect perturbed messages from the shuffler. The mechanism P_RR satisfies (ε, δ)-DP with optimal error value O((1/ɛ)), which means the computing binary summing up to additive error O((1/ɛ)) with constant probability.

 

5.5. Related works on DP-FL with shuffle model(s)

In real word, we have many tasks need a huge number of users to participate in the model e.g. (Microsoft, Apple, Google, .etc). So reducing the huge amount of noise in local model with achieving good privacy has inspired a current work for alternative models. For instance, ESA model that proposed by Bittau et al [Bittau et al. (2017)], has been presented a trusted SS to collect secure messages from users and perturbing it randomly before uploading to untrusted server.

Due to the importance of DP-FL-SS, it attracts lots of attention from academia and Industries [Balcer et al. (2020)]. Up to date, there are some published papers on this topic. For the local model, the famous example for that is the problem of privately summation of sum bounded real values among k different users, the center model achieved O (1) error [Cheu et al. (2019)]. While the local model achieves O ((1/ɛ)) error [Amos et al. (2008)], and recently Balle et al [Balle et al. (2019)], proves that the single message per participate can achieve only O (k)^1/3 MSE in local model. 

Since the privacy amplification plays a great role in implementing DP mechanism, the recent studies suggested many approaches that provide privacy amplification such as iteration [Xixi et al. (2020)] and subsampling [Balle et al. (2018)]. In [Cheu et al. (2019)], it focuses on amplification by shuffling to tradeoff between privacy in local model and accuracy in central model. It presents the single-message shuffle model with the analytic study of SS in distributed DP algorithms for summation of binary and real valued inputs. Its results are the summation of O ((1/ɛ)) messages per user suffice to achieve O (1) error in the curator model. In particular, it reduces the gap between LDP and CDP models by adding SS in between users and analyzers, which perturbs users’ messages before uploading it to analyzer. While SS can solve the private summation problem more correct than the local model. In [13], it focuses on single-message shuffle model protocols that provides the privacy blanket via shuffle model under setting randomizing then shuffling that copies k LDP with ɛ₀= O (log(k/ log(1=δ))) produces an ɛ = O (min(ε₀, 1)) e^ɛ0 . This protocol obtains better accuracy and communication than the proposed protocols by Cheu et al [Cheu et al. (2019)] for the same problem.

In [Erlingsson et al. (2019)], the privacy cost of LDP has been considered and it is much smaller than CDP view. It has showed that if the perturbed mechanism satisfies (ɛ_l, δ_l)- LDP, then it would satisfy  (ɛ_c, δ_c)- CDP with ɛ_c = O (ɛ_l). Consequently, ɛ_l was reduced to ɛ_c/. The most important achievements of shuffling is the privacy amplification by shuffling [Balle et al. (2019), Meehan et al. (2021), Erlingsson et al. (2019), Bittau et al. (2017)]. Where In the shuffle model, if the local randomized(R) satisfies (ɛ_l, δ_l)–LDP at ɛ_l ≤ log (k/log (1/δ_c))/2, Mechanism ℳ satisfies (ɛ_c, δ_c)-DP at ɛ_c = O (min (ɛ_l, 1) e^ɛl , where ɛ_l is the privacy budget in local model and ɛ_c is the privacy budget in center model.

In [Liu et al. (2020)], the subsampling in shuffle model has been considered to trade off between privacy and utility. In [Balle et al. (2018)], the privacy has been amplification by subsampling, if the mechanism ℳ : X^m→ Y satisfies (ɛ, δ)-DP, with respect to the replacement relationship on sets of size m, the mechanism ℳ satisfies (log (1+(m/k) (e^ε-1)), (m/k) δ)-DP, where m is number of subsampling, k is number of users. They proposed three different protocols (SS-simple protocol, SS-double protocol and top-k protocol) to randomize users’ data by implementing DP. The key difference between three protocols is the assumptions in random sub sampling. In SS-simple protocol, it assume that all dimensions are equally and this may discard important dimensions and occurring losses in sensitive users’ data. The practical result of this model provides an insufficient privacy amplification effect in FL for the data that has large dimensions. To fix this problem, SS-double protocol has been proposed to increase the privacy amplification by creating subsampling with m dimensions in each user data and each user perturbs m dimensions instead of perturbing one dimension in SS-simple protocol. Moreover, in order to boost the accuracy when the model size is larger than the user population, an advanced technique called SS-Topk has been proposed, which can solve SS-simple protocol and SS-double protocol problems. It selects top-k indexes with greatest absolute magnitudes over the input vector, this protocol boosting the privacy amplification with achieving the same privacy level.

In 2020 Borja Balle et al [Balle et al. (2020)], it studies a multi-message private summation in shuffle model which is a new technique for actual summation in the shuffle model. It improves the communication and accuracy by squeezing a single round protocol of multi message where the approximating sum from each subsequent message makes available the earned error estimation with the prior messages. This technique presents a direct tradeoff between the number of messages and the final accuracy sent by each user. By succeeding in reducing MSE to be as less as O ((log log k)²) where each user send O(loglog(k))messages and each message has a size O(log k).

According to our discussion of recent works about shuffle model through this section, we can say SS succeed in achieving high privacy in FL compared with LDP-FL and CDP-FL, because, besides shuffling step, SS requires from users to provide secure messages carefully. This is unlike with the global model. In global model, its responsibility is exclusively conducted by the reliable analyzer. In addition, from theoretical view, this model provides implementing easier mechanisms that are easy to explain, implement and verify. So we trust that DP-FL-SS is an interest for both theoretical and practical aspects.

 

 

 

6.     Conclusions

 FL has a greatly facilitated the progress and development of a huge amount data in machine learning by permitting for many users to participate in the model. For strong privacy in FL model, DP was broadly proposed to keep users’ data without data leaking during training process. The security of users’ data and the model updates are secured by LDP and CDP algorithms implementing during the training process. Both has their own specific weaknesses and strengths points. For instance, CDP is weaker to an adversary, whereas LDP can keep the users updates before transfer them to the analyzer. However, LDP is sensitive to noise, and higher noise can influence the model’s accuracy. So integrating differential privacy with federated learning is still not be the perfect solution. The recent studies suggest an intermediate model between users and analyzer to eliminate the weaknesses points in both DP and LDP by reducing the gap between privacy and utility. This intermediate model is called shuffle model. This paper provides a comprehensive survey of DP-FL-SS, including DP-FL-SS models, data statistics and the recent progress of private shuffle model from different aspects. Moreover we discussed the practical results of SS effect in exploring the gap between the local and curator model in DP-FL. We trust that our survey will be very important and urgent for future research in FL and also will help the newcomers to understand the complicated discipline of this active research zone.

 

REFERENCES

Aledhari M., Razzak R., Parizi R., Saeed F. (2020), Federated learning: a survey on enabling technologies, protocols, and applications, IEEE Access, 8, 140699-140725. Retreived from https://doi.org/10.1109/ACCESS.2020.3013541

Amos B., Kobbi N., and Eran O. (2008), Distributed private data analysis: Simultaneously solving how and what, 28th Annual International Cryptology Conference, Springer, 5157, 451-468.

Amos Beimel., Iftach Haitner., Kobbi Nissim. (2020), Uri Stemmer., On the Round Complexity of the Shuffle Model, arXiv: 2009.13510. Retreived from https://doi.org/10.1007/978-3-030-64378-2_24

Balcer V., Cheu A. (2019), Separating local & shuffled differential privacy via histograms, arXiv: 1911.06879.

Balle B., Barthe G., Gaboardi M. (2018), Privacy amplification by sub sampling: Tight analyses via couplings and divergences, ArXiv:1807.01647.

Balle B., Bell J., Gascon A., Nissim K. (2019), The privacy blanket of the shuffle model, arXiv: 1903.02837, Retreived from https://doi.org/10.1007/978-3-030-26951-7_22

Bittau A., Erlingsson U., Maniatis P., Mironov I., Raghunathan A., Lie D., Rudominer M., Kode U., Tinnes J., Seefeld B. (2017), PROCHLO: Strong privacy for analytics in the crowd. In Proceedings of the Symposium on Operating Systems Principles (SOSP), 441-459. Retreived from https://doi.org/10.1145/3132747.3132769

Borja Balle, James Bell, Adria Gascon, Kobbi Nissim (2019). Differentially Private Summation with Multi-Message Shuffling. arXiv:1906.09116v1 [cs.CR]. Retreived from https://doi.org/10.1145/3372297.3417242

Borja Balle., James Bell., Adrià Gascón., and Kobbi Nissim. (2020), Private Summation in the Multi-Message Shuffle Model. In Proceedings of the 2020ACM SIGSAC Conference on Computer and Communications Security ,Virtual Event, USA. 9-13, 2020. Retreived from https://doi.org/10.1145/3372297.3417242

C. Dwork. (2011), Affirm foundation for private data analysis, Communications of the ACM, 54(1), 86-95. Retreived from https://doi.org/10.1145/1866739.1866758

Casey Meehan., Amrita Roy Chowdhury., Kamalika Chaudhuri., Somesh Jha. (2021), A Shuffling frame work for local differential privacy, arXiv: 2106.06603v1.

Chen M., Yang Z., Saad W., Yin C., Poor H V., Cui S. (2021), A Joint Learning and Communications Framework for Federated Learning Over Wireless Networks. IEEE Transactions on Wireless Communications, 20(1), 269-283. Retreived from https://doi.org/10.1109/TWC.2020.3024629

Cheu A., Smith A., Ullman J., Zeber D., Zhilyaev M. (2019), Distributed differential privacy via shuffling, 11476, 375-403. Retreived from https://doi.org/10.1007/978-3-030-17653-2_13

David Byrd. (2020), Antigoni Polychroniadou., Differentially Private Secure Multi-Party Computation for Federated Learning in Financial Applications, arXiv: 2010.05867.

Ding B., Kulkarni J., Yekhanin S. (2017), Collecting telemetry data privately, in Adv. Neural Inf. Process. Syst., Long Beach, CA, 3571-3580.

Dwork C. (2006), Differential Privacy, Proceedings of the 33rd international conference on automata, languages and programming, 2, 1-12. Retreived from https://doi.org/10.1007/11787006_1

Dwork C. (2008), Differential privacy: a survey of results, International conference on theory and applications of models of computation, 4978, 1-19. Retreived from https://doi.org/10.1007/978-3-540-79228-4_1

Erlingsson Ú., Pihur, V., Korolova, A. (2014), Rappor: Randomized aggregable privacy-preserving ordinal response, Proceedings of the 2014 ACM SIGSAC Conference on computer and communications security, Scottsdale, AZ, USA, 1054-1067. Retreived from https://doi.org/10.1145/2660267.2660348

Farokhi., Farhad. (2021), Distributionally-robust machine learning using locally differentially-private data, springer Science and Business Media LLC. 1-13. Retreived from https://doi.org/10.1007/s11590-021-01765-6

Geyer R C., Klein T., Nabi M. (2020), Differentially Private Federated Learning: A Client Level Perspective, IEEE Access, 8, 140699-140725. Retreived from https://doi.org/10.1109/ACCESS.2020.3013541

Ghazi B., Golowich N., Kumar R., Manurangsi P., Pagh R., Velingker A., Pure differentially private summation from anonymous messages, arXiv:2002.01919, 2020. Retreived from https://doi.org/10.1007/978-3-030-45724-2_27

Ghazi B., Golowich N., Kumar R., Pagh R., Velingker A. (2020), On the power of multiple anonymous messages, arXiv:1908.11358.

Ghazi B., Golowich N., Kumar R., Manurangsi P., Pagh R., Velingker A. (2020), Pure differentially private summation from anonymous messages, arXiv:2002.01919.

Ghazi B., Manurangsi P., Pagh R., Velingker A.  (2020) Private aggregation from fewer anonymous messages. 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, Proceedings, 47,798-827. Retreived from https://doi.org/10.1007/978-3-030-45724-2_27

H. B. McMahan, D. Ramage, K. Talwar, and L. Zhang (2018), "Learning Differentially Private Recurrent Language Models," in arXiv:1710.06963 [cs].

H. B. McMahan., D. Ramage., Talwar K., Zhang L. (2018), Learning Differentially Private Recurrent Language Models, arXiv:1710.06963.

Hard A., Rao K., Mathews R., et al. (2018), Federated learning formable keyboard prediction. arXiv preprint arXiv:1811.03604.

Huang L., A. L. Shea., Qian H., Masurkar A., Deng H., Liu D. (2019), Patient clustering improves efficiency of federated machine learning to predict mortality and hospital stay time using distributed electronic medical records, J. Biomed. Informat, 99, 1-21. Retreived from https://doi.org/10.1016/j.jbi.2019.103291

Huang Xixi., Ding Ye., Jiang Zoe L., Qi Shuhan., Wang Xuan., Liao Qing. (2020), DP-FL: a Novel differentially private federated learning framework for the unbalanced data World Wide Web-internet and Web Information Systems, 23(4), 2529-2545. Retreived from https://doi.org/10.1007/s11280-020-00780-4

Jiang L., Tan R., Lou X., Lin G. (2019), On lightweight privacy preserving collaborative learning for Internet-of-Things objects, in Proc. Int. Conf. Internet Things Design Implement., 70-81. Retreived from https://doi.org/10.1145/3302505.3310070

Jordan Awan., Aleksandra Slavkovi'c. (2018), Structure and Sensitivity in Differential Privacy: Comparing K-Norm Mechanisms, arXiv:1801.09236.

Kairouz P., McMahan H B., et al. (2021) Advances and Open Problems in Federated Learning. Foundations and Trends in Machine Learning, 14(1), 1-119. Retreived from https://doi.org/10.1561/2200000083

Li T., Sahu K., Talwalkar A., Smith V. (2020), Federated learning challenges, methods, and future directions, IEEE Signal Processing Magazine, 37(3), 50-60. Retreived from https://doi.org/10.1109/MSP.2020.2975749

Li W., Milletarì F.,Xu D.,Rieke N .,Hancox J., Zhu W., Baust M., Cheng Y .,Ourselin S.,J C M ., Feng A. (2019), Privacy-preserving federated brain tumor segmentation, in Proc. Int. Workshop Mach. Learn. Med. Image, 11861,133-141. Retreived from https://doi.org/10.1007/978-3-030-32692-0_16

Liu D., Miller T., Sayeed R., Mandl K. (2018), FADL: Federated autonomous deep learning for distributed electronic health record, arXiv:1811.11400.

Liu F. (2019) Generalized Gaussian Mechanism for Differential Privacy, in IEEE Transactions on Knowledge and Data Engineering, 31, 747-756. Retreived from https://doi.org/10.1109/TKDE.2018.2845388

Liu R., Cao Y. , Chen H., Guo R., Yoshikawa M. (2020), FLAME: Differentially Private Federated Learning in the Shuffle Model, arXiv:2009.08063.

McMahan H., Moore E., Ramage D., Hampson S., and Arcas B. (2016), Communication efficient learning of deep networks from decentralized data, arXiv:1602.05629.

Nakamoto S. (2019), Bitcoin: A Peer-to-Peer Electronic Cash System.Manubot;Online. Retreived from https://metzdowd.com.

NhatHai Phan., Xintao Wu., Han Hu., Dejing Dou. (2017), Adaptive Laplace Mechanism: Differential Privacy Preservation in Deep Learning" IEEE International Conference on Data Mining 17, 2374-8486.

Qi Liu., Juan Yu., Jianmin Han., Xin Yao. (2021), Differentially private and utility-aware publication of trajectory data, Expert Systems with Applications, 180, 1-14. Retreived from https://doi.org/10.1016/j.eswa.2021.115120.   

Ramaswamy S.,Mathews R., Rao K., Beaufays F. (2019), Federated learning for emoji prediction in amobile keyboard, arXiv:1906.04329.

Ren J., Wang H., Hou T., Zheng S., Tang C. (2019), Federated learning-based computation offloading optimization in edge computing supported Internet of Things, IEEE Access, 7, 69194-69201. Retreived from https://doi.org/10.1109/ACCESS.2019.2919736.

Sarfaraz., Aaliya., Chakrabortty., Ripon K., Essam., Daryl L. (2021), A tree structure-based improved block chain framework for a secure online bidding system, 102, 1-20. Retreived from https://doi.org/10.1016/j.cose.2020.102147

Ulfar Erlingsson., Vitaly Feldman., Ilya Mironov., Ananth Raghunathan., Kunal Talwar. (2019), and Abhradeep Thakurta., Ampliffication by shuffling: From local to central differential privacy via anonymity. the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, 2468-2479. Retreived from https://doi.org/10.1137/1.9781611975482.151

Victor Balcer., Albert Cheu., Matthew Joseph., and Jieming Mao. (2020), Connecting robust shuffle privacy and pan-privacy. arXiv:2004.09481. Retreived from https://doi.org/10.1137/1.9781611976465.142

Vitaly Feldman., Ilya Mironov., Kunal Talwar., Abhradeep Thakurta. (2018), Privacy amplification by iteration, In 59th IEEE Annual Symposium on Foundations of Computer Science, Paris, France, 521-532. Retreived from https://doi.org/10.1109/FOCS.2018.00056

Wei K., et al. (2020), "Federated Learning With Differential Privacy: Algorithms and Performance Analysis," in IEEE Transactions on Information Forensics and Security, 15, 3454-3469. Retreived from https://doi.org/10.1109/TIFS.2020.2988575

Yang Q., Liu Y., Chen T., et al. (2019), Federated machine learning: concept and applications, ACM Transactions on Intelligent Systems and Technology, 10(2), 1-19. Retreived from https://doi.org/10.1145/3298981

Yang T., Andrew G., Eichner H., et al. (2018), Applied federated learning: improving google keyboard query suggestions, arXiv:1812.02903.

Zhao L., Wang Q., Zou Q., Zhang Y., Chen Y. (2020), Privacy-Preserving Collaborative Deep Learning With Unreliable Participants, in IEEE Transactions on Information Forensics and Security, 15, 1486-1500. Retreived from https://doi.org/10.1109/TIFS.2019.2939713

Zhao. P., Zhang, G., Wan, S., Liu, G., Umer, T. (2019), A survey of local differential privacy for securing internet of vehicles. J. Supercomputer, 76, 1-22. Retreived from https://doi.org/10.1007/s11227-019-03104-0

Zhu T., Ye D., Wang W., Zhou W., Yu P. (2020), More Than Privacy: Applying Differential Privacy in Key Areas of Artificial Intelligence, IEEE Transactions on Knowledge and Data Engineering. doi: 10.1109/TKDE.2020.3014246. Retreived from https://doi.org/10.1109/TKDE.2020.3014246