Improving the Response of Permanent Magnet Synchronous Motors to Disturbances Using PSO Techniques

 

Ahmed Alfadli ¹, Ameer Kamoona ²,  Zaid Alhadrawi ³

 

¹ Ministry of Education, 66001 Al Muthanna, Iraq

² Computers System Department, Al-Furat Al-Awsat Technical University,51015 Babil, Iraq

³ Department of Electrical Engineering, Faculty of Engineering, University of Kufa, Najaf, Iraq

 

1. INTRODUCTION

Today, many sustainable energy sources are used as an alternative to traditional ones due to the expanded need for energy consumption. As a result of this concept, the power-consuming device must be carefully designed and controlled for efficient use of energy. Electrical motors may be categorized as a big part of the total electrical loads because of their growth use in domestic and industrial applications Luo & Liu (2019), Thike (2020). After the use of permanent magnets in the manufacturing of motors, the PMSM motor becomes the most usable one compared with the other types due to its superior properties of high efficiency and energy saving as well as cost Mutluer & Bilgin (2012), it can be considered of less effected by harmonic content as compared to other synchronous machines such as generators. Since that intervention, this motor has passed through many steps of enhancement in the main structure, design, and controller to improve its performance. The motor controller can be considered the most vital component in motor optimization; hence it is based on PI controller which is a feedback mechanism used for many years in industrial applications Ahn et al. (2021)-Kim et al. (2021). The PI determines an error, that is, the disparity between the reading process and set-point value. The controllers diminish these distinctions by modulating the process control inputs.

A group of perfect parameters (Proportional) P and (Integral) I may produce a perfect reply involving the rise, settling, overshoot times plus steady-state errors Yang & Wang (2009),Štulrajter et al. (2007). One of the main difficulties in using this controller is obtaining the optimum values of P and I, to overcome this problem popular optimization algorithms can be used Kareem et al. (2021), such as Particle Swarm Optimization (PSO). The optimization research has focused on the PMSM design for several benefits such as cogging torque reduction as well as ripple torque, in addition to motor weight reduction and better motor efficiency. Based on the design optimization criteria, a lot of independent parameters have been identified. Moreover, the selection of the input design parameters plays a role in increasing design sensitivity. All of these previous aspects have been investigated in papers Mutluer & Bilgin (2012)-Ahn et al. (2021), and other design optimization ways were discussed also. On the other hand, some researchers deal with parameter optimization of PMSM such as Liu et al. (2016), hence this work depends on (SVPWM) Space Vector Pulse Width Modulation for ripple mitigation. In Sui et al. (2018), the Moth-Flame Optimization Algorithm has been used for the same previous purpose. In this paper, a series of extensive simulation cases have been done to determine and analyze the performance of PMSM under different conditions, followed by an enhancement of motor effectiveness by optimizing the PI parameters with PSO, hence a comparison has been introduced between motor response for manual calculation of PI parameter vs PSO adjustment one in two cases, which are starting and sudden change in motor operating conditions (i.e. speed and load).

 

2. MATERIALS AND METHODS

In this work, the motor type which is used as surface-mounted type of pure induced EMF with 3 stator coils besides permanent magnets has mounted on the surface of the motor rotor, there are some suppositions that have been used to achieve the PMSM model Dal et al. (2019)-Suryakant et al. (2018): Cancellation of the saturation machine core losses are negligible and no dynamic current field. According to the above points, the stator voltage equation can be mathematical modelling as a d-q axis as below:

=  -                                                                 (1)

=  -                                                                (2)

The equations of stator flux linkage:                                            

Where: rs : Stator resistance, id ,iq ∶ d-q stator current, λd  ,λq ∶ d-q axis flux linkage of the stator, Ld  ,Lq ∶ d-q axis inductance (Ld= Lq), λm: Flux linkage by permanent magnets in the rotor.

The Synchronous speed can be written by

 =                                                                              (5) 

   

Hence: wr, p is the rotor speed in (rad/sec) and the number of poles in turn. By substituting (3) and (4) into (1) and (2), we get:

 = -   +  +                                        (6)

 

 = -   +  - +                         (7)

The electromagnetic torque is given by the following formula:

 = ( ) (  -  )                                                     (8)

Substituting (3) and (4) in (8), assuming that inductances (L_d= L_q) we get:

 = ( ) ( )                                                       (9)

Then with load torque is given by:

  =  +J                                             (10)

 

Where:  Te, T1, B, J are electromagnetic torque, mechanical load torque, mechanical damping coefficient and moment of inertia, respectively. This model will be implemented in MATLAB/Simulink and subjected to the performance investigation with the two cases of optimized PI controller and POS optimized one under starting with load or changing in motor operating conditions to emulate a disturbance case.

 

3. RESULTS AND SIMULATION

The simulation procedure was built depending on two aspects. The first one is to emulate the performance of PMSM using the conventional PI controller based on trial and error by applying various types of disturbances to the motor to investigate and record its behavior. Secondly, the application of the proposed optimized PI controller parameters based on POS to the motor model to find the system performance enhancement that may appear such as speed, and torque ripple mitigation. The simulation model has been achieved in the MATLAB/Simulink environment as depicted in Figure 1 It contains a three-phase PMSM of 1.1 kW, 220 V, 3000 rpm rated, which is fed by a PWM inverter.

Figure1

Figure 1 MATLAB/Simulink Model for the PMSM

 

The inverter is built with basic blocks that are available in the Simulink library, and its gain is controlled by VSC (Voltage Source Converter) and then directed to the stator of the motor. The PMSM has been implemented with a sinusoidal back EMF, which is modeled in the dq reference, while a trapezoidal machine with abc reference. The connection of the stator winding is a star with neutral. And Table 1 shows the PMSM parameters. On the other hand, in the case of the PI controller tuned by the PSO algorithm. The PSO algorithm parameters that have been used to achieve better motor performance are shown in Table 2 below.

Table 1

Table 1 Parameter of PMSM
d-axis inductance (Ld)	q-axis inductance (Lq)	Stator phase resistance Rs	Armature inductance (H)	Number of poles (P)	Moment of inertia (J)	Friction factor F (N.m.s)	Speed
0.0085 H	0.0085 H	2.875 Ω	0.00153 H	2	0.0008 kg.m2	0	3000 rpm

 

Table 2

Table 2 PSO Parameters
“Swarm size (number of birds)”	“Number of iterations”	“Cognitive coefficient (C1)”	“Social coefficient (C2)”	“Inertia weight (W)”
5	20	1.2	1.2	0.8

 

A comparison has been made between PMSM responses (i.e., speed, torque, and starting current) for the two above-described tuning methods considering different motor operation conditions, which are starting and sudden disturbance. The test cases can be classified as below.

1)    Motor starts to load

For the first simulation case of a motor starting with a load (i.e. torque) of 3 N.m. applied to the motor shaft and a speed of 700 rpm. The values of the PI controller gains (Kp, Ki) were (2.6, 50), (0.85, 0.95) for manual tuning by trial and error and optimal tuning by PSO respectively. The results in Figure 2 illustrate the speed with and without PSO. Besides, Figure 3 depicts the PI controller speed error for both methods.

Figure 2

 

Figure 2 Speed of Motor (RPM), Case1

 

Figure 3

Figure 3 Speed Error PI Controller, Case1

 

The torque result in both cases is considered also. Figure 4 shows a comparison between the electromagnetic torque ripple with and without PSO. For more focus on the differences, Figure 5 is the enlarged scale of the electromagnetic torque ripple of Figure 4 It is clear from the figure that the ripple of the torque has been eliminated drastically in case PI is tuned by PSO.

 

Figure 4

 

Figure 4 Electromagnetic Torque, Case1

 

Figure 5

Figure 5 Enlarged Scale of Electromagnetic Torque Ripple, Case1

 

A comparison between motor stator current is presented in Figure 6, which shows the enhancement in the line stator current of the motor for the case of the controller tuned by the PSO method.

 

Figure 6

Figure 6 Line Stator Current, Case1

 

 

2)    Changes during motor operation

In this simulation case, the motor was tested with a fixed load of 3 N.m., and the speed was suddenly changed from 400 to 700 RPM at a step time of 0.03 sec. during motor operation as a form of disturbance. The values of the PI controller gain (Kp, Ki) were (2.6, 50), (1.13, 0.93) for manual tuning by trial and error, and the optimal one tuned by PSO respectively. The motor has been analyzed as the former case and the results are depicted in Figure 7, Figure 8, Figure 9, Figure 10

Figure 7

 

Figure 7 Speed of Motor (RPM), Case2

 

Figure 8

Figure 8 Speed Error Ip Controller, Case2

 

Figure 9

 

Figure 9 Electromagnetic Torque, Case2

 

 

Figure 10

Figure 10 Stator Current of the Motor, Case2

 

Next, the motor was tested with a fixed speed of 700 rpm, and the load torque was suddenly changed from 2 to 4 N.m. at step time 0.04 sec. as a form of disturbance. The values of the PI controller gains (Kp, Ki) were (2.6, 50), (1.33, 0.592) for manual tuning by trial and error and optimal tuning by PSO respectively. Figure 11,Figure 12,Figure 13,Figure 14 show the motor performance in this case.

Figure 11

 

Figure 11 Speed of Motor (RPM), Case3

 

Figure 12

Figure 12 Speed Error IP Controller, Case3

 

Figure 13

 

Figure 13 Electromagnetic Torque, Case3

 

Figure 14

 

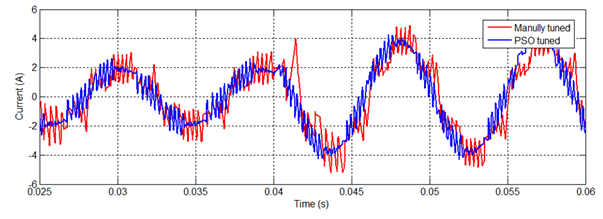
Figure 14 Stator Current, Case3

 

 

4. Discussion

Regarding the findings. They are all supporting suppositions of better motor performance in the case of using PSO for tuning the gains of the PI controller. The proposed optimization method was able to cope with a wide range of motor operation conditions and achieve the desired enhancements. The results are classified in two test cases as below:  

 

·        The motor starts to load

 The results of motor speed performance which are depicted in Figure 2, Figure 3, explain that the use of PI controller based on PSO will reduce the settling time and eliminate the overshooting of the speed response, as it becomes smooth with little ripple. The boost in PMSM performance with the PSO method can be observed in more depth through the data in Table 3.

Tables 3

Table 3 Settling Time, Rise Time, and Overshoot with Both Methods
Controller	Rise time (sec)	Settling time (sec)	Overshoot
PI based trial and error	0.006	0.025	2.77%
PI based PSO	0.006	0.006	0

 

We can see that in the case of the manual method, there is an overshoot percent of 2.77%, whereas it is zero in the case of the PSO method. Moreover, the same evaluation can be applicable in using the torque results in Figure 4,Figure 5. The value of torque ripple in time 0.01 sec was compared with the controller adjusted by the traditional method and based on Particles Swarm Optimization (PSO) provided in Table 4 The percentage of ripple falls is almost 95.4% in comparison with a tune-by manual method.

Table 4

Table 4 Torque Ripple Reduction The ripple of the Torque PSO not considered PSO considered Tmax Tmin 22 1

 

Besides the speed and torque, the motor current also showed a more stable trajectory with PSO placed than without, as in Figure 6. According to the above findings, we can assume that the use of PSO could be successful totally to bringing the motor to smooth starting with load.

·        Changes during motor operation

In this case, we have assumed two states of disturbance represented by sudden changes in speed and torque (i.e., motor load). Referring to Figure 7,Figure 8,Figure 9,Figure 10,Figure 11,Figure 12,Figure 13,Figure 14, again, the PSO method showed a nearly perfect performance and could be considered much better compared to the manual method.

 

5. CONCLUSION

This study has presented a PI-PSO-based observer aimed at enhancing the performance of Permanent Magnet Synchronous Motors (PMSMs). The conventional approach to tuning PI controller parameters is often time-consuming and lacks the precision required for optimal motor control. To overcome these limitations, Particle Swarm Optimization (PSO) was employed to efficiently determine the optimal controller gains. The PSO technique demonstrated rapid convergence and reduced computational effort. Simulation results confirm that the proposed method significantly improves motor performance, evident through reduced steady-state error in speed response and minimized torque ripple. Additionally, the system exhibited enhanced robustness and operational efficiency, validating the effectiveness of the PI-PSO control strategy in handling dynamic disturbances and improving overall motor stability.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Ahn, J.-M., Son, J.-C., & Lim, D.-K. (2021). Optimal Design of Outer-Rotor Surface-Mounted Permanent Magnet Synchronous Motor for Cogging Torque Reduction Using Territory Particle Swarm Optimization. Journal of Electrical Engineering & Technology, 16(1), 429–436. https://doi.org/10.1007/s42835-020-00599-z    

Cho, S.-K., Jung, K.-H., & Choi, J.-Y. (2018). Design Optimization of Interior Permanent Magnet Synchronous Motor for Electric Compressors of Air-Conditioning Systems Mounted on EVs and HEVs. IEEE Transactions on Magnetics, 54(11), 1–5. https://doi.org/10.1109/TMAG.2018.2849078   

Cui, J., Xiao, W., Zou, W., Liu, S., & Liu, Q. (2020). Design Optimisation of Submersible Permanent Magnet Synchronous Motor by Combined DOE and Taguchi Approach. IET Electric Power Applications, 14(6), 1060–1066. https://doi.org/10.1049/iet-epa.2019.0346   

Dal, Ö., Yıldırım, M., & Kürüm, H. (2019). Optimization of Permanent Magnet Synchronous Motor Design by Using PSO. 2019 4th International Conference on Power Electronics and their Applications (ICPEA), 1–6. https://doi.org/10.1109/ICPEA1.2019.8911192    

Gao, J., Dai, L., & Zhang, W. (2018). Improved Genetic Optimization Algorithm with Subdomain Model for multi-objective Optimal Design of SPMSM. CES Transactions on Electrical Machines and Systems, 2(1), 160–165. https://doi.org/10.23919/TEMS.2018.8326463   

Izanlo, A., Gholamian, S. A., & Abdollahi, S. E. (2020). Optimal Design of a Permanent Magnet Synchronous Motor for High Efficiency and Low Cogging Torque. International Journal on Electrical Engineering and Informatics, 12(2), 173–186. https://doi.org/10.15676/ijeei.2020.12.2.1   

Kamoona, A. A., Alfadli, A. N., Alshabeeb, I. A., & AlKhafaji, A. S. (2021). Harmonic Reduction of a Synchronous Generator in a Wind Energy System. Current Applied Science and Technology, 271–282.

Kareem, H. Z. A., Mohammed, H. H., & Mohammed, A. A. (2021). Robust Tuning of Power System Stabilizer Parameters Using the Modified Harmonic Search Algorithm. IIUM Engineering Journal, 22(1), 47–57. https://doi.org/10.31436/iiumej.v22i1.1276

Kim, J.-H., Cha, K.-S., & Hwang, S.-W. (2021). Analysis of Effect of the Magnetization Distribution of multi-pole PM on SPMSM Performance Using Equivalent Magnetic Circuit Considering Dead Zone. Department of Automotive Engineering, Hanyang University, Seoul, Korea.

Kim, S., Lee, S.-G., Kim, J.-M., Lee, T. H., & Lim, M.-S. (2020). Robust Design Optimization of Surface-Mounted Permanent Magnet Synchronous Motor Using Uncertainty Characterization by Bootstrap Method. IEEE Transactions on Energy Conversion, 35(4), 2056–2065. https://doi.org/10.1109/TEC.2020.3004342   

Li, Y., Zhu, C., Wu, L., & Zheng, Y. (2019). Multi-objective Optimal Design of High-Speed Surface-Mounted pErmanent Magnet Synchronous Motor for Magnetically Levitated Flywheel Energy Storage System.IEEE Transactions on Magnetics, 55(7), 1–8. https://doi.org/10.1109/TMAG.2019.2906994   

Liu, X., Du, J., & Liang, D. (2016). Analysis and Speed Ripple Mitigation of a Space Vector Pulse Width Modulation-Based Permanent Magnet Synchronous Motor with a Particle Swarm Optimization Algorithm. Energies, 9(11), 923. https://doi.org/10.3390/en9110923   

Luo, Y., & Liu, C. (2019). Multi-Vector-Based Model Predictive Torque Control for a Six-Phase PMSM motor with fixed switching frequency. IEEE Transactions on Energy Conversion, 34(3), 1369–1379. https://doi.org/10.1109/TEC.2019.2917616

Mutluer, M., & Bilgin, O. (2012). Design Optimization of PMSM by Particle Swarm Optimization and Genetic Algorithm. 2012 International Symposium on Innovations in Intelligent Systems and Applications, 1–4. https://doi.org/10.1109/INISTA.2012.6247024

Mutluer, M., & Bilgin, O. (2012). Design Optimization of PMSM by Particle Swarm Optimization and Genetic Algorithm. 2012 International Symposium on Innovations in Intelligent Systems and Applications, 1–4. https://doi.org/10.1109/INISTA.2012.6247024

Pulvirenti, M., Scarcella, G., Scelba, G., Testa, A., & Harbaugh, M. M. (2017). On-line Stator Resistance and Permanent Magnet Flux Linkage Identification on Open-End Winding PMSM drives.University of Catania Catania, IEEE. https://doi.org/10.1109/ECCE.2017.8096971

Sain, C., Biswas, P. K., & Banerjee, A. (2015). Design and Analysis of open Loop Model of a Permanent Magnet Synchronous Motor (PMSM) drive. Siliguri Institute of Technology Siliguri, IEEE.

Soygenc, O. C., & Ergene, L. T. (2020). Particle Swarm Optimization Implementation on PMSM design. 2020 21st International Symposium on Electrical Apparatus & Technologies (SIELA), 1–4. https://doi.org/10.1109/SIELA49118.2020.9167068   

Sui, Y., Zheng, P., Tang, P., Wu, F., & Wang, P. (2018). A Five-Phase 20-slot/18-pole PMSM for Electric vehicles. International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 35(2), 439–455. https://doi.org/10.1108/COMPEL-02-2015-0106    

Suryakant, S., Sreejeth, M., & Singh, M. (2018). Performance analysis of PMSM drive using hysteresis current controller and PWM current controller. Electrical Engineering Department, Delhi Technological University, India, IEEE.

Thike, R. (2020). Mathematical Model of an Interior PMSM with Aligned Magnet and Reluctance Torques. University of Canberra, IEEE.

Yang, M., & Wang, X. (2009). Fuzzy PID Controller Using Adaptive Weighted PSO for Permanent Magnet Synchronous Motor Drives. 2009 Second International Conference on Intelligent Computation Technology and Automation, 2, 736–739. https://doi.org/10.1109/ICICTA.2009.413

You, Y.-M., & Chung, D.-W. (2017). Optimal Design of a Permanent Magnet Synchronous Motor to Improve Torque and Demagnetization Characteristics. Journal of Magnetics, 22(3), 423–429. https://doi.org/10.4283/JMAG.2017.22.3.423

Zawarczyński, Ł., & Stefański, T. (2019). Parametric Identification of PMSM Mathematical Model. Kielce University of Technology, IEEE.

Štulrajter, M., Hrabovcova, V., & Franko, M. (2007). Permanent Magnets Synchronous Motor Control Theory. Journal of Electrical Engineering, 58(2), 79–84.