|
|
|
|
Control and identification of controlled auto-regressive moving average (CARMA) form of an introduced single-input single-output tumor model
Kiavash Hossein Sadeghi 1![]()
![]() ,
Abolhassan Razminia 2
,
Abolhassan Razminia 2![]()
![]() ,
Abolfazl Simorgh 3
,
Abolfazl Simorgh 3![]()
![]()
1 Department
of Electrical Engineering, Faculty of Intelligent Systems Engineering and Data
Science, Persian Gulf University, Bushehr 75169, Iran
2 Department
of Electrical Engineering, Faculty of Intelligent Systems Engineering and Data
Science, Persian Gulf University, Bushehr 75169, Iran
3 Department
of Aerospace Engineering, Universidad Carlos III de Madrid, 28911 Leganés, Spain
|
|
ABSTRACT |
||
|
The article
investigates the parameter estimation for controlled auto-regressive moving
average models with gradient based iterative approach and two-stage gradient
based iterative approach. Since deriving a new model for tumor model is
substantial, introduced system identification algorithms are used in order to estimate parameters of a specific nonlinear
tumor model. Besides, in order to estimate tumor
model a collection of output and input data is taken from the nonlinear
system. Apart from that, effectiveness of the
identification algorithms such as convergence rate and estimation error is depicted through various tables and figures. Finally,
it is shown that the two stage approach has higher
identification efficacy. |
|||
|
Received 05 January 2024 Accepted 04 February 2024 Published 20 February 2024 Corresponding Author Abolhassan
Razminia, razminia@pgu.ac.ir DOI 10.29121/ijetmr.v11.i2.2024.1403 Funding: This research
received no specific grant from any funding agency in the public, commercial,
or not-for-profit sectors. Copyright: © 2024 The
Author(s). This work is licensed under a Creative Commons
Attribution 4.0 International License. With the
license CC-BY, authors retain the copyright, allowing anyone to download,
reuse, re-print, modify, distribute, and/or copy their contribution. The work
must be properly attributed to its author.
|
|||
|
Keywords: Gradient Based
Iterative Algorithms, 2-STAGE Identification, System Identification,
Parameter Estimation, Tumor Model |
|||
1. INTRODUCTION
The iterative and recursive algorithms could be used to solve matrix equations Wang (2007), Ding (2005), Xie (2010), parameter estimation problems Li (2018), Li (2018), Liu (2010) and filtering issues Ma (2020). In parameter estimation approaches which are recursive, the estimation of parameters can to be calculated in an online framework Du (2017), Wei (2017). On the other hand, the primary notion of the hierarchical algorithms is to update estimation of the parameters by applying a set of data Ding (2018), Ding (2019), Sadeghi (2023). The hierarchical parameter estimation approaches make adequate use of all output and input Data Li (2020), Wang (2020), and could enhance the accuracy of estimation of parameters Li (2020), Ding (2020) and convergence rate of parameters Li (2021), Chen (2020).
Two-stage
algorithms have an enormous usage in the realm of parameter identification Sadeghi (2023), Sadeghi (2023) developed a two-stage
step-wise system identification approach for a class of nonlinear dynamic
systems Li
et al. (2006). In Raja
(2015), two-stage least mean
square adaptive methods relying on process of fractional signal were fostered
regarding CARMA systems. A two-stage neural network
algorithms related to ARMA model estimation by the use of a
simple mean called extended sample autocorrelation function is presented
Lee
(1994). In Bin
(2012), a two-stage method is
introduced regarding the system identification of an ARMAX model which
identifies ARX and MA part separately by bias-eliminated least squares
method and another basic method respectively. Also in Ding
(2020), a new two-stage
algorithm for estimating parameter of system is brought up but in this article
as a novelty, a CARMA system is discussed.
Having a suitable model for tumor system has become an integral issue since the death rate of cancer has become considerable. Accessing a suitable polynomial model for tumor can make the designing of a controller for system much easier. In Pillis (2020), a four population model is presented which contains tumor cells, host cells, drug interaction, immune cells and a controller based on optimization, which is used to satisfy the specific desire. In Sweilam & AL-Mekhlafi (2018), an updated nonlinear mathematical format of a general tumor beneath immune suppression is discussed. The brought up model in this paper is ruled by a fractional differential equations system. Lobato (2016) presented another model for tumor and in their works they aim to reach a protocol of optimization for injection of drug to sick individuals having cancer, by the making both of the cells having cancer and the drug concentration which has been prescribed minimum Lobato (2016). Tumor model presented in this last research is the basis of our study throughout the rest of the paper.
Controlling a CARMA or ARMAX model system has been the subject of a few papers and not much work has been done in this field. For instance, In Chen & Guo (1987), an optimal adaptive control for ARMAX systems using a quadratic loss function is introduced. In Li (2021), abrupt faults in ARMAX models have been taken into consideration and reliable control problem has been studied. Multivariable system control is discussed in Osorio-Arteaga (2020) where a robust adaptive control is applied to ARMA and ARMAX structures of an electric arc model. Furthermore, linear neural networks was set as a study tool for adpative control of CARMA systems Watanabe (1992).
In the following section, a nuance characteristic of the system configuration regarding the CARMA configuration is brought up. Also, section section 3 includes the mathematics of two novel GI algorithm. Section 4 describes a specific tumor model. In section 5, all the necessary simulations for showing the effectiveness of new algorithms are illustrated by identifying a tumor model. Eventually, in the last section, all the outcomes were derived.
2. System model: Carma systems
Take the introduced below CARMA system into consideration:
![]()
Here u(t) is the succession of input of the system, y(t)
is the succession of output of the
system and ![]() is a
succession of white noise with zero mean and variance
is a
succession of white noise with zero mean and variance ![]() Also A(q), B(q) and c(q) are multinomial
in the monad backward variation agent [i.e.
Also A(q), B(q) and c(q) are multinomial
in the monad backward variation agent [i.e. ![]() For simplicity in the rest of the paper, we
have the following notations: A =: X describes A is described as X; The
indication I (
For simplicity in the rest of the paper, we
have the following notations: A =: X describes A is described as X; The
indication I (![]() )
is an identity matrix with suitable dimensions (
)
is an identity matrix with suitable dimensions (![]() $1_{n}$
indicates a vector of n-dimensional column
which all components are 1. The superscript T indicates the transpose of
a matrix; the matrix
norm is described by
$1_{n}$
indicates a vector of n-dimensional column
which all components are 1. The superscript T indicates the transpose of
a matrix; the matrix
norm is described by ![]() .
.
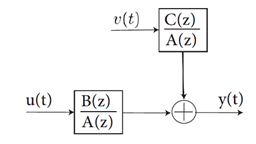
Now look at the CARMA system shown in Figure
\ref{fig.1}. We define A(q), B(q) and C(q) as polynomials of known orders ![]() as
as
follows:
![]()
![]()
![]()
In a generic way, it is presumed that y(t) = 0, u(t) = 0
and ![]() =
0 for t
=
0 for t ![]() 0. Take
0. Take ![]() ,
Consider the system parameter vectors:
,
Consider the system parameter vectors:
![]()
![]()
![]()
and the corresponding information vectors:
![]()
![]()
![]()
![]()
Based on the above definitions and equation (\ref{eq.1}), we attain the the below parameter estimation configuration:
![]() =
=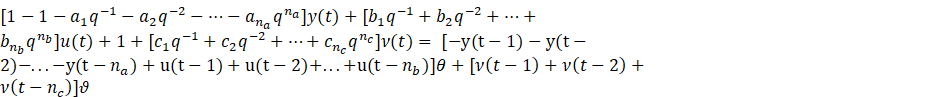 ,
,
y(t)= ![]() +
+
![]() +
+ ![]() , (2)
, (2)
y(t)= ![]() +
+ ![]() , (3)
, (3)
3. Theory of identification and
control algorithms
3.1. Gradient based iterative
algorithms(GI)
We consider k=1,2,3,… as an
hierarchical variable ![]() and
and
![]() as
the hierarchical identification of and
while k iteration has established. Beyond that
as
the hierarchical identification of and
while k iteration has established. Beyond that ![]() is the biggest eigenvalue of the matrix of
symmetric format X.
is the biggest eigenvalue of the matrix of
symmetric format X.
Now we take an array of data with length L which works
with the model introduced in. Here, we consider the vector of stacked output
data Y(L) and matrix of the stacked data
![]() like:
like:
Y(L):=
![]() :=
:=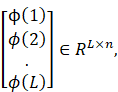
Now we define the static criterion function as follows:
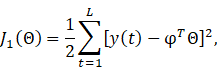
which can be equally described as:
![]()
By taking advantage of negative gradient probe,
calculating the partial derivative of ![]() regarding
regarding ![]() ,
we attain this iterative relation:
,
we attain this iterative relation:
![]()
=![]()
![]()
Here, ![]() is a convergence factor or an iterative
step-size. To make sure about convergence of
is a convergence factor or an iterative
step-size. To make sure about convergence of ![]() ,
all the eigenvalues of
,
all the eigenvalues of ![]() should be in the monad circle, so
should be in the monad circle, so ![]() therefore as suitable conservative form of
therefore as suitable conservative form of ![]() we have:
we have:
![]()
As to eschew calculating the intricate eigenvalues of a matrix which is square and to decrease evaluation expense, the trace of matrix is taken advantage of and capitalized on a different manner for picking up the convergence rate:
![]()
Now it is possible to attain the gradient based iterative method for CARMA system presented in equation (1) with the following set of equations:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
The steps of calculating ![]() from
equation (4)-(10) summarized as below:
from
equation (4)-(10) summarized as below:
1) Regarding
![]() set every variable to zero. Assume k = 1, take
the data length L (L
set every variable to zero. Assume k = 1, take
the data length L (L![]() and
take the primary amounts,
and
take the primary amounts, ![]() and the system identification precision
and the system identification precision ![]() .
.
2) Gather all the input u(t) and output y(t) for t=1,2,…,L.
3) Attain
the vectors of information ![]() by equation (9),
by equation (9), ![]() by equation (10) and
by equation (10) and ![]() by equation (8).
by equation (8).
4) Form
the vector of stacked output Y(L) regarding equation (6) and the matrix of
stacked information ![]() regarding equation (7), also pick up a large
regarding equation (7), also pick up a large ![]() based on equation (5).
based on equation (5).
5) Upgrade the parameter estimation vector $\hat{\Theta}{k}$ by equation (\ref{eq.4}).
6) Contrast
![]() with
with ![]() .
If
.
If ![]() extend
k in unit order and start from step 5. In all other respects, attain iteration
k and the system identification vector
extend
k in unit order and start from step 5. In all other respects, attain iteration
k and the system identification vector ![]() .
.
3.2. Two-stage Gradient based iterative algorithms (2S-GI)
Consider the CARMA model described in equation (\ref{eq.2}).
First, we define these two imaginary output variables:
![]()
![]()
Afterwards by these definitions we have:
![]() (11)
(11)
![]() (12)
(12)
Take $L$ as data length. According to equation (11) and (12), we define these two static criterion functions:
![]() (13)
(13)

Consider the vector of stacked output Y(L), vectors of the
stacked imaginary outputs ![]() and
and ![]() ,
and the matrices of stacked information
,
and the matrices of stacked information ![]() and
and ![]() are as follows:
are as follows:
![]()
![]()
![]()
![]()
![]()
Equations (13) and (14) can be equivalently written as:
![]()
![]()
By taking advantage of the search of negative gradient to make the criterion functions above minimum, we have:
![]()
![]()
![]()
=![]()
![]()
![]()
![]()
![]()
![]()
To make sure about convergence of ![]() and
and ![]() all the eigenvalues of
all the eigenvalues of ![]() and
and ![]() ,
should be in the unit circle, so we have:
,
should be in the unit circle, so we have:
![]()
![]()
Therefore, similar to GI algorithm as a conservative choice, we have
the following relation for ![]() and
and ![]()
![]()
![]()
In brief, we have the following set of equations for 2S-GI algorithm:
![]() (15)
(15)
![]() (16)
(16)
![]()
![]()
![]()
![]() (20)
(20)
![]()
![]() (22)
(22)
![]()
![]() (24)
(24)
![]() (25)
(25)
The steps of attaining ![]() and
and![]() included in the 2S-GI approach from
equation (15)–(25) are brought up as follows:
included in the 2S-GI approach from
equation (15)–(25) are brought up as follows:
1) Regarding
![]() ,
put every parameter to 0. Imagine k=1 take the length of data as L (
,
put every parameter to 0. Imagine k=1 take the length of data as L (![]() and set the initial values as:
and set the initial values as: ![]() and the parameter estimation accuracy
and the parameter estimation accuracy ![]()
2) Gather
all the input u(t) and output y(t) for t=1,2,…,L.
Attain the information vectors ![]() (22)
by equation (22) and
(22)
by equation (22) and ![]() (t)
by equation (23).
(t)
by equation (23).
3) Build
the vector of stacked output Y(L) by (19) and the matrices of stacked
information ![]() and
and ![]() by (20) and (21), calculate the convergence
factor
by (20) and (21), calculate the convergence
factor ![]() and
and ![]() regarding (16) and (18).
regarding (16) and (18).
4) Update
the vectors of parameter approximation ![]() by
by
(15) and (17).
5) Compare
![]() with
with
![]() and
and
![]() with
with ![]() :If
:If
![]() +
+![]() >
>
![]() ,
extend k by $1$ and start from step 4. In all other respects attain iteration k
and the vectors of estimation of parameters
,
extend k by $1$ and start from step 4. In all other respects attain iteration k
and the vectors of estimation of parameters ![]() and
and
![]() .
.
4. Control theory
In this part of the paper, theory of a ziegler nichols PID controller for third order processes introduced in (Bobal, 2006) is brought up. The control law which we took advantage of is:
![]() (26)
(26)
![]()
Here ![]() is the controller error. The feedback form of
control law is:
is the controller error. The feedback form of
control law is:
![]() (28)
(28)
Where ![]() respectively are:
respectively are:
![]()
![]()
![]()
And we have:
![]() .
.
And ![]() are ultimate period and ultimate gain
respectively.
are ultimate period and ultimate gain
respectively.
5. Tumor model
I indicate the immune cells number at time t, T denotes the tumor cells number at time t, N describes the normal (host) cells number at time t, and u is the plan of control.\begin{figure}[h] \centering \includegraphics[width=.5\linewidth]{T-I-N.eps} \caption{Random tumor and immune cells interactions.}
![]() ,
,
![]()
![]()
![]() .
.
Values of known parameters in above equations are listed below Lobato (2016)
Parameter |
Values |
Parameter |
Values |
0.3 |
|||
0.1 |
1 |
||
1 |
0.5 |
||
1 |
0.5 |
||
1 |
1 |
||
0.2 |
0.01 |
||
1.5 |
1 |
||
S |
0.33 |
|
|
Therefore, we yield: \begin{equation*} \begin{split}
![]() ,
,
![]() ,
,
![]() .
.
6. Simulations
6.1. Estimation of T(t)
In this paper, we aim to identify T(t) as the quantity of tumor cells at time t and I(t) as the quantity of immune
cells at time t, by presenting novel parameter estimation method. In
simulations assume ![]() ,
,
![]() and
and
![]() .
In simulations,
.
In simulations,![]() ,
,
![]() =1
and
=1
and ![]() =1.
\subsection{Estimation of T(t)}
=1.
\subsection{Estimation of T(t)}
The CARMA model of T(t) as the output and u(t) as the input is:
![]()
![]()
![]()
Table 1
|
Table 1
Estimation Result for |
||||
|
Algorithms |
t=L |
|
|
|
|
1000 |
-0.1005 |
-0.8864 |
-1.7053 |
|
|
GI |
2000 |
-0.0970 |
-0.8816 |
-1.7751 |
|
3000 |
-0.0974 |
-0.8822 |
-1.7473 |
|
|
1000 |
-0.0976 |
-0.8835 |
-1.7570 |
|
|
2S-GI |
2000 |
-0.0946 |
-0.8836 |
-1.7145 |
|
3000 |
-0.0921 |
-0.8797 |
-1.7161 |
|
|
True value |
-0.0862 |
-0.8937 |
-1.7580 |
|
|
Algorithms |
t=L |
|
|
|
|
1000 |
1.7859 |
-0.0460 |
-0.0020 |
|
|
GI |
2000 |
1.7389 |
0.0229 |
0.0426 |
|
3000 |
1.7378 |
0.0231 |
0.0009 |
|
|
1000 |
1.7690 |
0.0019 |
-0.0030 |
|
|
2S-GI |
2000 |
1.7380 |
0.0281 |
-0.0189 |
|
3000 |
1.7726 |
0.0455 |
-0.0485 |
|
|
1.7570 |
0.6264 |
-0.3459 |
|
Algorithms |
t=L |
|
|
1000 |
7.6604 |
|
|
GI |
2000 |
6.8844 |
|
3000 |
6.4698 |
|
|
1000 |
6.8316 |
|
|
2S-GI |
2000 |
6.2351 |
|
3000 |
5.7110 |
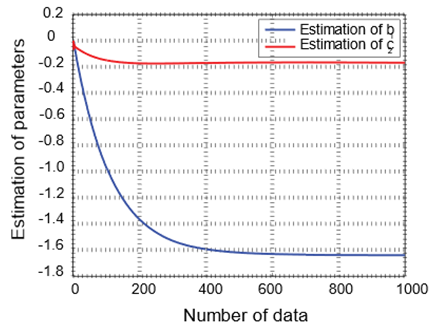
|
Estimation of |

|
Estimation of |
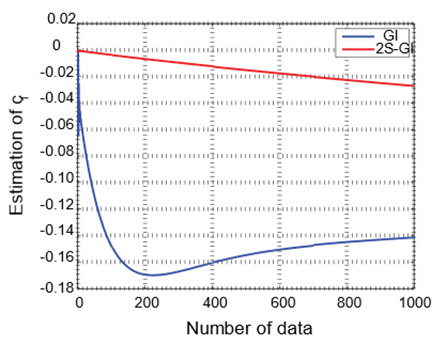
|
Estimation of |
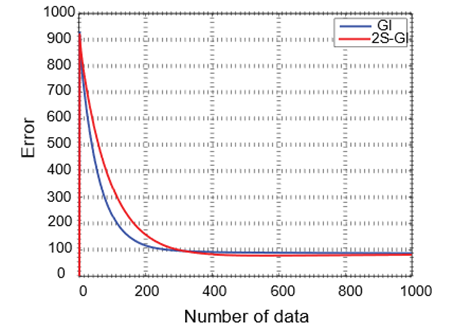
|
Estimation Error for CARMA System with Variance |
Table 2
|
Table 2
Estimation Results for |
||||
|
Algorithms |
t=L |
|
|
|
|
1000 |
-0.1182 |
0.8405 |
-1.6400 |
|
|
GI |
2000 |
-0.1412 |
-0.8478 |
-1.7594 |
|
3000 |
-0.136 |
-0.8474 |
-1.7737 |
|
|
1000 |
-0.1379 |
-0.8400 |
-1.6632 |
|
|
2S-GI |
2000 |
-0.1332 |
-0.8451 |
-1.6933 |
|
3000 |
-0.1270 |
-0.8465 |
-1.7573 |
|
|
True value |
-0.0862 |
-0.8937 |
-1.7580 |
|
|
Algorithms |
t=L |
|
|
|
|
1000 |
1.8659 |
-0.1413 |
-0.1693 |
|
|
GI |
2000 |
1.9069 |
0.0147 |
0.0319 |
|
3000 |
1.8679 |
0.0142 |
0.0082 |
|
|
1000 |
1.9208 |
-0.0274 |
0.0265 |
|
|
2S-GI |
2000 |
1.8392 |
0.0123 |
-0.0094 |
|
3000 |
1.8060 |
0.0385 |
-0.0566 |
|
|
1.7570 |
0.6264 |
-0.3459 |
|
Algorithms |
t=L |
|
|
1000 |
8.6731 |
|
|
GI |
2000 |
6.7497 |
|
3000 |
6.9010 |
|
|
1000 |
8.1050 |
|
|
2S-GI |
2000 |
6.2351 |
|
3000 |
5.8114 |
6.2. Estimation of I(t)
The CARMA model of $I(t)$ as the output and u(t) as the input is:
![]()
![]()
![]()
Table 3
|
Table 3
Estimation Results for |
||||
|
Algorithms |
t=L |
|
|
|
|
1000 |
-1.042 |
0.0541 |
0.8791 |
|
|
GI |
2000 |
-0.9243 |
-0.0612 |
-0.8699 |
|
3000 |
-0.9436 |
-0.0405 |
-0.9078 |
|
|
1000 |
-0.9297 |
-0.05 |
-0.8541 |
|
|
2S-GI |
2000 |
-0.941 |
-0.0471 |
-0.8699 |
|
3000 |
-0.127 |
-0.8465 |
-1.7573 |
|
|
True value |
0.9499 |
-0.0345 |
-0.8921 |
|
|
Algorithms |
t=L |
|
|
|
|
1000 |
0.8782 |
-0.1586 |
0.0987 |
|
|
GI |
2000 |
0.7725 |
0.0158 |
-0.0080 |
|
3000 |
0.7917 |
0.0165 |
0.0248 |
|
|
1000 |
0.7871 |
-0.0219 |
-0.0229 |
|
|
2S-GI |
2000 |
0.7537 |
0.0324 |
0.0342 |
|
3000 |
0.7697 |
-0.0238 |
0.0200 |
|
|
1.7570 |
0.6264 |
-0.3459 |
|
Algorithms |
t=L |
|
|
1000 |
3.7344 |
|
|
GI |
2000 |
3.0066 |
|
3000 |
2.3635 |
|
|
1000 |
2.9884 |
|
|
2S-GI |
2000 |
2.1040 |
|
3000 |
1.9732 |
Table 4
|
Table 4
Estimation Results for |
||||
|
Algorithms |
t=L |
|
|
|
|
1000 |
-0.9189 |
-0.0712 |
-0.8799 |
|
|
GI |
2000 |
-0.8958 |
-0.0928 |
-0.9277 |
|
3000 |
-0.9008 |
-0.0857 |
-0.8848 |
|
|
1000 |
-0.9282 |
-0.0555 |
-0.8405 |
|
|
2S-GI |
2000 |
-0.9542 |
-0.0366 |
-0.9301 |
|
3000 |
-0.1270 |
-0.8465 |
-1.7573 |
|
|
True value |
-0.9175 |
-0.0647 |
-0.8817 |
|
|
Algorithms |
t=L |
|
|
|
|
1000 |
0.6899 |
-0.0324 |
0.0286 |
|
|
GI |
2000 |
0.8068 |
0.0209 |
0.0159 |
|
3000 |
0.8065 |
-0.0254 |
-0.0163 |
|
|
1000 |
0.6995 |
0.0206 |
-0.0171 |
|
|
2S-GI |
2000 |
0.8130 |
0.0207 |
-0.0189 |
|
3000 |
0.7981 |
0.0217 |
0.0273 |
|
|
1.7570 |
0.6264 |
-0.3459 |
|
Algorithms |
t=L |
|
|
1000 |
4.039 |
|
|
GI |
2000 |
3.3538 |
|
3000 |
2.8344 |
|
|
1000 |
3.8944 |
|
|
2S-GI |
2000 |
2.5776 |
|
3000 |
2.2446 |
7. Control of tumor models
The final goal of this research is to make the amount of tumor cells minimum, therefore we
take T(t)=0 as the desired output of the system. Based on control theory
introduced in the third section and the identified polynomial model of T(t),
the ultimate period and ultimate gain is ![]() and
and ![]() Therefore
Therefore ![]() and
and ![]() and
and ![]() .
.
The output and input of the feedback form is depicted in the next two figures.
From tables and figures above, the below results are derived:
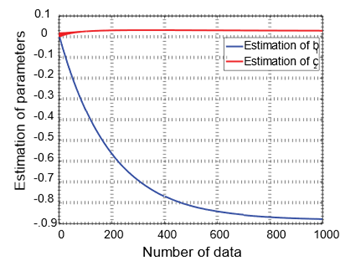
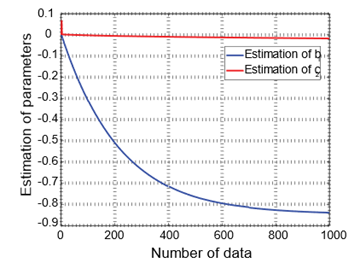
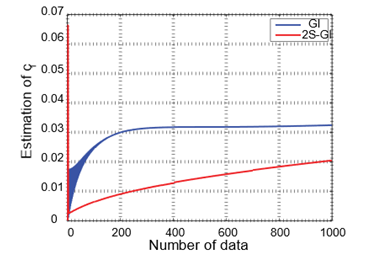
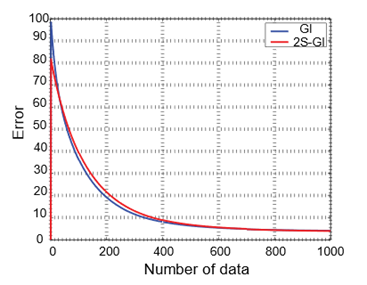
· The system identification errors of the GI and 2S-GI approaches decrease as the data length increases.
· 2S-GI method, compared to GI method, produces less error and therefore is more effective at estimating parameters.
· As the noise to ratio signal rises, both introduced algorithms produce a larger amount of error.
· From figures, it is perceived that both introduced algorithms converge at a final point and have a competent convergence rate.
· The introduced controller proved that, it is able to make the amount of tumor cells in a specific period of time minimum.
8. Conclusion
In this contribution, mathematical theories and algorithms of two identification methods of GI and 2S-GI for CARMA systems were developed. GI is an old method but 2S-GI is a novel method which introduced in this paper. Furthermore, a tumor model with one input and three outputs were presented by works of other scholars. By means of introduced parameter estimation approaches, the model were identified. Above that, by taking advantage of a ziegler nichols PID controller the amount of tumor cells were controlled and it was illustrated that the controller could minimize amount of tumor cells in a specific span of time. Also, the GI and 2S-GI algorithm showed that they both are able to estimate parameter of a polynomial CARMA configuration in fast convergence rate and by producing an insignificant amount of error.
CONFLICT OF INTERESTS
None.
ACKNOWLEDGMENTS
None.
REFERENCES
Bin, X. I. (2012). A Two-Stage ARMAX Identification Approach Based on Bias-Eliminated Least Squares and Parameter Relationship Between MA Process and Its Inverse. Acta Automática Sinica, 491-496. https://doi.org/10.1016/S1874-1029(11)60310-8
Bobál, V. E. (2006). Digital Self-Tuning Controllers: Algorithms, Implementation and Applications. Springer Science & Business Media.
Chen, H.-F., & Guo, L. (1987). Optimal Adaptive Control and Consistent Parameter Estimates for ARMAX Model with Quadratic Cost. SIAM Journal on Control and Optimization, 845-867. https://doi.org/10.1137/0325047
Chen, J. Q. (2020). Modified Kalman Filtering Based Multi-Step-Length Gradient Iterative Algorithm for ARX Models with Random Missing Outputs. Automatica. https://doi.org/10.1016/j.automatica.2020.109034
De Pillis, L. G. (2001). A Mathematical Tumor Model with Immune Resistance and Drug Therapy: An Optimal Control Approach. Computational and Mathematical Methods in Medicine, 79-100. https://doi.org/10.1080/10273660108833067
Ding, F. A. (2005). Gradient Based Iterative Algorithms for Solving a Class of Matrix Equations. IEEE Transactions on Automatic Control, 1216-1221. https://doi.org/10.1109/TAC.2005.852558
Ding, F. E. (2019). Gradient-Based Iterative Parameter Estimation Algorithms for Dynamical Systems from Observation Data. Mathematics. https://doi.org/10.3390/math7050428
Ding, F. E. (2020). Gradient Estimation Algorithms for the Parameter Identification of Bilinear Systems using the Auxiliary Model. Journal of Computational and Applied Mathematics. https://doi.org/10.1016/j.cam.2019.112575
Ding, F. E. (2020). Two-Stage Gradient-Based Iterative Estimation Methods for Controlled Autoregressive Systems using the Measurement Data. International Journal of Control, Automation and Systems, 886-896. https://doi.org/10.1007/s12555-019-0140-3
Ding, F. E. (2018). Iterative Parameter Identification for Pseudo-Linear Systems with ARMA Noise Using the Filtering Technique. IET Control Theory and Applications. https://doi.org/10.1049/iet-cta.2017.0821
Du, D. E. (2017). A Novel Networked Online Recursive Identification Method for Multivariable Systems with Incomplete Measurement Information. IEEE Transactions on Signal and Information Processing over Networks, 744-759. https://doi.org/10.1109/TSIPN.2017.2662621
Ji, Z. E. (2020). An Attention-Driven Two-Stage Clustering Method for Unsupervised Person Re-Identification. Computer Vision-ECCV 2020: 16th European Conference. https://doi.org/10.1007/978-3-030-58604-1_2
Lee, J. K. (1994). A Two-Stage Neural Network Approach for ARMA Model Identification with ESACF. Decision Support Systems. https://doi.org/10.1016/0167-9236(94)90019-1
Li, K., Peng, J.-X., & Bai, E.-W. (2006). A Two-Stage Algorithm for Identification of Nonlinear Dynamic Systems. Automatica, 1189-1197. https://doi.org/10.1016/j.automatica.2006.03.004
Li, L. Z. (2020). A Two-Stage Maximum a Posterior Probability Method for Blind Identification of LDPC Codes. IEEE Signal Processing Letters, 111-115. https://doi.org/10.1109/LSP.2020.3047334
Li, M. A (2018). The Least Squares Based Iterative Algorithms for Parameter Estimation of a Bilinear System with Autoregressive Noise Using the Data Filtering Technique. Signal Processing, 23-34. https://doi.org/10.1016/j.sigpro.2018.01.012
Li, M. A. (2018). Auxiliary Model Based Least Squares Iterative Algorithms for Parameter Estimation of Bilinear Systems using Interval-Varying Measurements. IEEE Access, 21518-21529. https://doi.org/10.1109/ACCESS.2018.2794396
Li, M. A. (2020). Maximum Likelihood Least Squares Based Iterative Estimation for a Class of Bilinear Systems using the Data Filtering Technique. International Journal of Control, Automation and Systems, 1581-1592. https://doi.org/10.1007/s12555-019-0191-5
Li, M. A. (2021). Maximum Likelihood Hierarchical Least Squares-Based Iterative Identification for Dual-Rate Stochastic Systems. International Journal of Adaptive Control and Signal Processing, 240-261. https://doi.org/10.1002/acs.3203
Liu, Y. D. (2010). Least Squares Based Iterative Algorithms for Identifying Box-Jenkins Models with Finite Measurement Data. 1458-1467. https://doi.org/10.1016/j.dsp.2010.01.004
Lobato, F. S. (2016). Determination of an Optimal Control Strategy for Drug Administration in Tumor Treatment using Multi-Objective Optimization Differential Evolution. Computer Methods and Programs in Biomedicine, 51-61. https://doi.org/10.1016/j.cmpb.2016.04.004
Ma, H. E. (2020). Partially-Coupled Gradient-Based Iterative Algorithms for Multivariable Output-Error-Like Systems with Autoregressive Moving Average Noises. IET Control Theory and Applications, 2613-2627. https://doi.org/10.1049/iet-cta.2019.1027
Osorio-Arteaga, F. J.-D. (2020). Robust Multivariable Adaptive Control of Time-Varying Systems. IAENG International Journal of Computer Science, 605-612.
Raja, M. A. (2015). Two-Stage Fractional Least Mean Square Identification Algorithm for Parameter Estimation of CARMA Systems. Signal Processing, 327-339. https://doi.org/10.1016/j.sigpro.2014.06.015
Sadeghi, K. H. (2023). Efficient Identification Algorithm for Controlling Multivariable Tumor Models: Gradient-Based and Two-Stage Method. Advanced Mathematical Models and Applications, 8(2), 185-198.
Sadeghi, K. H. (2023). Multi-Innovation Iterative Identification Algorithms for CARMA Tumor Models. International Review on Modelling and Simulation. https://doi.org/10.15866/iremos.v16i2.23270
Sadeghi, K. H. (2023). Utilizing ARMA Models for System Identification in Stirred Tank Heater: Different Approaches. Computing Open. https://doi.org/10.1142/S2972370123300030
Sweilam, N. H., & AL-Mekhlafi, S. M. (2018). Optimal Control for a Nonlinear Mathematical Model of Tumor Under Immune Suppression: A Numerical Approach. Optimal Control Applications and Methods, 1581-1596. https://doi.org/10.1002/oca.2427
Wang, L. E. (2020). Decomposition-Based Multiinnovation Gradient Identification Algorithms for a Special Bilinear System Based on its Input-Output Representation. International Journal of Robust and Nonlinear Control, 3607-3623. https://doi.org/10.1002/rnc.4959
Wang, M. X. (2007). "Iterative Algorithms for Solving the Matrix Equation AXB+ CXTD= E.". Applied Mathematics and Computation, 622-629.
Watanabe, K. T. (1992). An Adaptive Control for CARMA Systems Using Linear Neural Networks. International Journal of Control, 483-497. https://doi.org/10.1080/00207179208934324
Wei, Z. E. (2017). Online Model Identification and State-of-Charge Estimate for Lithium-Ion Battery with a Recursive Total Least Squares-Based Observer. IEEE Transactions on Industrial Electronics, 1336-1346.
Xie, L. Y. (2010). Gradient Based and Least Squares Based Iterative Algorithms for Matrix Equations AXB+ CXTD= F. Applied Mathematics and Computation, 2191-2199. https://doi.org/10.1016/j.amc.2010.07.019
|
|
 This work is licensed under a: Creative Commons Attribution 4.0 International License
This work is licensed under a: Creative Commons Attribution 4.0 International License
© IJETMR 2014-2024. All Rights Reserved.


