MASSIVE PARTICLE TUNNELING RATE OF KERR-NEWMAN-ANTI-DE SITTER BLACK HOLE BY HAMILTON-JACOBI METHOD

 

M. Ilias Hossain ¹, M. Jakir Hossain ¹

 

¹ Professor, Department of Mathematics, Rajshahi University, Rajshahi - 6205, Bangladesh

 

1. INTRODUCTION

Recently, a semiclassical tunnelling process applied to find the Hawking radiation of the static Schwarzschild and Reissner-Nordstr¨om black holes by Parikh and Wilczek Parikh and Wilczek (2000), Parikh (2002), Parikh (2004) and their result shows that the radiation spectrum is not pure thermal but satisfies the unitary principle and support the result of information conservation. In their process, the tunneling potential barrier is produced by the self-gravitation interaction and the position of the horizons before and after the particle’s emission. Following this method, several researchers studied the Hawking radiation of various spacetime Hemming and Keski-Vakkuri (2001), Arzano et al. (2005), Medved  (2002), Medved (2002), Medved and Vagenas (2005), Medved and Vagenas  (2005), Vagenas (2002), Vagenas (2003), Shankaranarayanan et al. (2002), Angheben et al. (2005) by using Painleav´e or dragging or tortoise or Eddington-Finkelstein coordinate transformations and these radiations are limited to uncharged massless particle only.

In this article, we use the Parikh and Wilczek’s opinion Parikh and Wilczek (2000), Parikh (2002), Parikh (2004) and employing standard Hamilton-Jacobi method to investigate the Hawking non-thermal and purely thermal tunneling rates of the Kerr-Newman-anti-de Sitter (KNAdS) black hole for massive particle. In order to carry-over this article, KNAdS black hole spacetime is described as follows. The Kerr-Newman anti-de Sitter (KNAdS) black hole which is the KAdS black hole generalized with a charge parameter, described by the metric

 

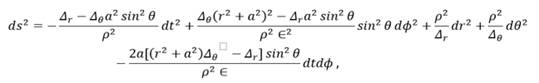     Equation 1

  

 

Where

, , ,                      Equation 2

 

Here the parameters  and q are the associated with the mass, angular momentum, cosmological radius, and charge parameters of the spacetime respectively in the background of the rotating anti de Sitter space. The spacetime causal structure depend strongly on the singularities of the metric given by the zeros of  as follows

 

                                 Equation 3

 

Depending on the black hole parameters, the function  with  has four distinct roots. For the KNAdS black hole case we are interested to find the real root of , namely the real root  corresponds to the radius of the black hole’s outer event horizon, while the other real root  represents the radius of the inner cauchy horizon and  as the cosmological horizon. Equation (3) can be written as

 

        Equation 4   

 

 

Solving the above equation, the position of the black hole horizons is given by   

 

Equation 5

 

and                                               

Equation 6

 

where  ,

              .                                                Equation 7

 

and  is the another cosmological horizon. With  the black hole horizon can be approximated as

 

                               Equation 8

 

Taking only the positive sign which is the event horizon of KNAds black hole as follows

 

                                Equation 9

 

Expanding  in terms of black hole parameters with negative cosmological constant under the condition, we obtain

 

                                        Equation 10

 

which can be written as

 

                                 Equation 11

 

Now if we set  then  with  and hence the event horizon of KNAds black hole is less than Kerr-Newmann Chen and Yang (2007) event horizon  As the event horizon of KNAds black hole coincides with the outer infinite red-shift surface, we apply the geometrical optical limit and the “s-wave” approximation. Using the semiclassical WKB method Massar and Parentani (2000), the tunneling probability is found to be related to the imaginary part of the action of the following form

 

,                                                                                             Equation 12

 

where I is the action of the radiating particle and is the emission rate.

The later section describes near the event horizon the new line element of KAdS black hole.  In section 3 and 4, we derived the Hawking non thermal and thermal radiation respectively. In section 5, we present our results and discussion.  Finally, in section 6, we present our concluding remarks.

 

2. The HJ Method for KNAdS Spacetime

The Hamilton-Jacobi method was applied extensively to the non-thermal radiation in 1990s and attracted people’s attention Srinivasan and Padmanabhan (1999), Angheben et al. (2005), Kerner and Mann (2007). In 2005, applying semiclassical tunneling method, Angheben, Nadalini, Vanzo and Zerbini Angheben et al. (2005) developed Hamilton-Jacobi method Shankaranarayanan et al. (2001), Shankaranarayanan et al. (2002), Shankaranarayanan (2003), Srinivasan and Padmanabhan (1999), Padmanabhan (2004) ignoring the self-gravitational effect of the emitted scalar particles. Here we now consider the method of Chen et al. Chen and Yang (2007), Chen et al. (2008) to calculate the imaginary part of the action from the relativistic Hamilton-Jacobi equation. The action of the radiating particle I satisfies the relativistic Hamilton-Jacobi equation

 

                                                                                             Equation 13

 

where m and  are the mass of the particle and the inverse metric tensors respectively.

In this method, we avoid the exploration of the equation of motion in the Painlev´e coordinates systems for calculate the imaginary part of the action I. For the convenience of our research to study the Hawking radiation, adopting the transformation  on the line element (1), we obtain the new line element of the Kerr-Newman-anti-de Siter black hole as

 

                                              Equation 14

 

The position of black hole horizon of the metric given by Eq. (14) is same as given in Eq. (11). Therefore, the line element near the event horizon rewritten as

 

          ,        Equation 15

 

where  and  are defined as follows

 

 and                         Equation 16

 

Calculating the non-null inverse metric tensors from the metric (15) and employing these in Eq. (13) as follows

 

Equation 17

 

To solve action , we consider the properties of the black hole spacetime and carry out the separation of variables as

 

Equation 18

 

where  is the energy of the emitted particle,  and  are the generalized momentums, and  s the angular momentum of the particle with respect to -axis. Inserting Eq. (18) into Eq. (17) to seek a solution of the following form

 

 

Equation 19

 

where the angular velocity of the particle at the event horizon is

 

Equation 20

 

We treat the emitted particle as an ellipsoid shell of energy  to tunnel across the event horizon. Finishing the above integral by using the Cauchy’s integral formula, we obtain

 

Equation 21

 

where  sign comes from the square root. Therefore, the imaginary part of the action  corresponding to the outgoing particle is obtained by  times the residue of the integrand

 

Equation 22

 

Using Eqs. (11) and (20) into Eq. (22), we get the imaginary part of the true action of the radiation particle as

 

where .

where  and .

 

To get the maximum value of the integration, neglecting higher order terms above and equal  in the denominator, we then get

Equation 23

 

3. Non-thermal Tunneling Rate

Since the emitted particle can be treated as a shell of energy ω, Eqs. (22) and (23) should be modified when the particle’s self-gravitational interaction is incorporated. Taking into account the energy conservation as well as angular momentum, the mass parameter and the angular momentum in these equations will be replaced with  and  when the particle with energy ω and angular momentum j tunnels out of the event horizon. We fix the ADM mass, charge and angular momentum of the total spacetime and in presence of comological constant KNAdS spacetime is dynamic and allow mass and angular momentum of the black hole to fluctuate. Then the imaginary part of the true action can be calculated from Eq. (23) in the following integral

 

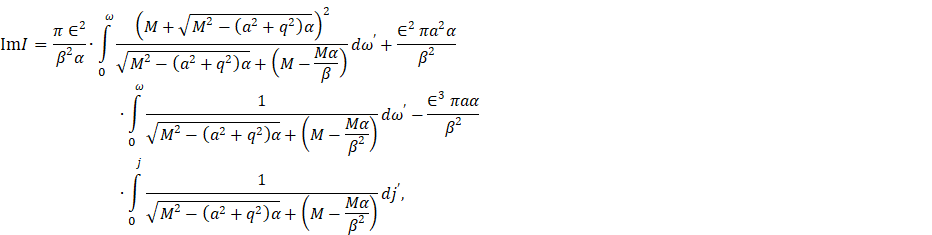
Equation 24

 

For the maximum value of integration, neglecting . Equation (24) becomes

 

Equation 25

 

Replacing  and  by  and  respectively, we obtain

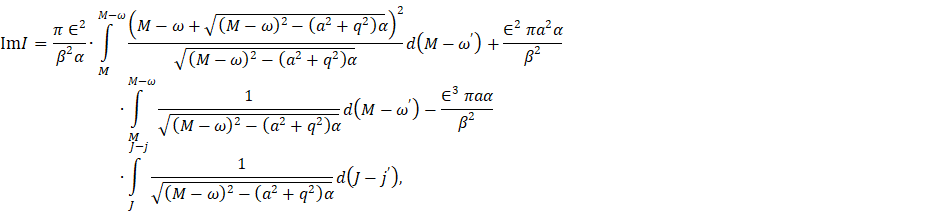
Equation 26

 

where  and so there is

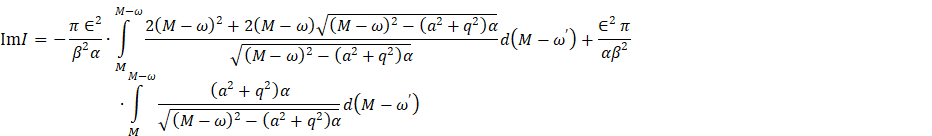
Equation 27

 

Finishing the  integral, we obtain

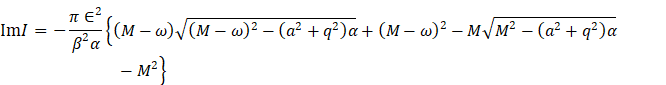
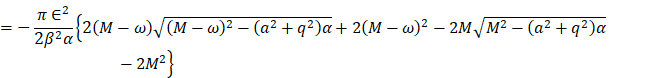
Equation 28

 

Therefore, the non-thermal tunnelling rate for the KNAdS black hole is given by

 

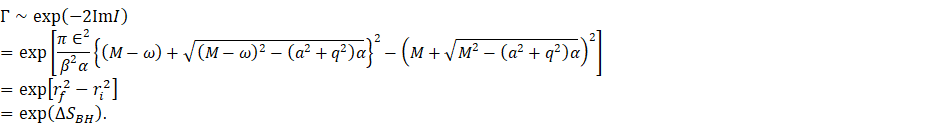
Equation 29

 

Here we find that  is the change of Bekenstein-Hawking entropy of the KNAdS black hole before and after the massive particles emission by taking into account  and .

 

4. Purely Thermal Radiation

The radiation spectrum given by Eq. (29) is not pure thermal, which gives a correction to the Hawking radiation of the KNAdS black hole and is consistent with an underlying unitary theory. We now expand (29) in power of  upto second order as discussed by Hossain et al. Hossain and Rahman (2013) of the form

 

Equation 30

 

From Eq. (10.29), we can write

 

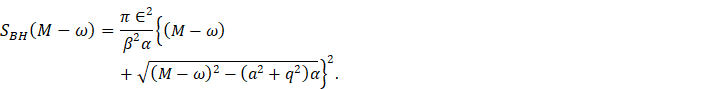
Equation 31

 

Using Eq. (31) in Eq. (30), we obtain

 

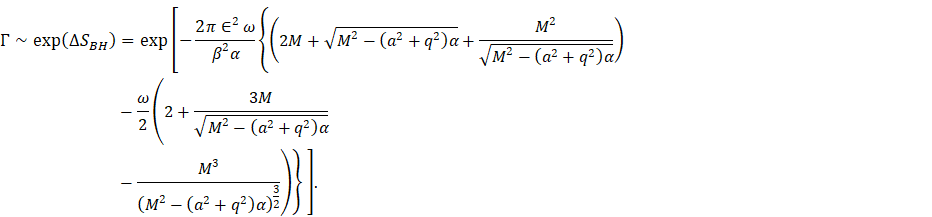
Equation 32

 

If we put  in the place of , the Hawking non-thermal spectrum and pure thermal spectrum agree with that of KNdS black hole.

 

5. results and discussion

The results we have obtained in this articler provides further evidence to support the Parikh and Wilczek’s opinion Parikh and Wilczek (2000), Parikh (2002), Parikh (2004) from spherically symmetric black holes. The study of this article gives the result for the Kerr-Newman black hole Chen and Yang (2007)  when . For , the study provides the result for the Kerr-anti-de Sitter black hole Hossain (2017), while for , the result reduces for the Kerr black hole Zhang and Zhao (2005). The result for the Schwarzschild-anti-de Sitter black hole Rahman and Hossain, (2013) is obtained if one sets  and . Moreover, the choice  and  gives the result for the Schwarzschild black hole Parikh and Wilczek (2000).

 

6. Conclusion

In a nutshell, we have investigated the Hawking non-thermal and purely thermal radiations of massive particles as a semiclassical tunneling process from the KNAdS black hole event horizon by taking into account the self-gravitation effect of the emitted particles, the unfixed background spacetime. The results of our work show that the radiant spectrum is not a pure thermal one and the tunneling rate is related to the change of Bekenstein-Hawking entropy and is consistent with an underlying unitary theory.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Angheben, M., Nadalini, M., Vanzo, L., and Zerbini, S. (2005). arXiv:hep-th/0503081; Nadalini M., Vanzo L. and Zerbini S., J. Hawking Radiation as Tunnelling for Extremal and Rotating Black Holes :JHEP. Journal of Physics A – Mathematical and General39, 0505, 014, 6601 (2006). https://doi.org/10.1088/1126-6708/2005/05/014.

Arzano, M., Medved, A. J. M., and Vagenas, E. C. (2005). hep-th/0505266. Hawking Radiation as Tunnelling Through the Quantum Horizon. Journal of Hepatology, 0509, 037. https://doi.org/10.1088/1126-6708/2005/09/037.

Chen, D. Y., and Yang, S. Z. (2007). Hawking radiation of the Kerr–Newman Black Hole. International Journal of Theoretical Physics, 46(12), 3067–3071. https://doi.org/10.1007/s10773-007-9420-4.

Chen, D. Y., Zu, X. T., and Yang, S. H. (2008). Massive Particle Tunnels from the Taub-Nut Black Hole. Acta Physica Polonica. Part B, 39(6), 1329.

Hemming, S., and Keski-Vakkuri, E. (2001). Gr-qc/0005115. Hawking Radiation from AdS Black Holes. Physical Review. Part D, 64(4), 044006. https://doi.org/10.1103/PhysRevD.64.044006.

Hossain, M. I. (2017). Hawking Non-Thermal and Purely Thermal Radiations of Rotating Black Hole in Anti-De Sitter Spacetime by Hamilton–Jacobi Method. GANIT: Journal of Bangladesh Mathematical Society, 37, 99–109 (ISSN. 1606, 3694). https://doi.org/10.3329/ganit.v37i0.35729.

Hossain M. I. and Rahman M. A. (2013). Hawking Nonthermal and Thermal Radiations of Reissner-Nordstr¨om Anti-De Sitter Black Hole by Hamilton–Jacobi Method. Astrophysics and Space Science, 347(1), 91–97. https://doi.org/10.1007/s10509-013-1505-3.

Kerner, R., and Mann, R. B. (2007). Tunnelling from G¨odel Black Holes. Physical Review. Part D, 75(8), 084022. https://doi.org/10.1103/PhysRevD.75.084022.

Massar, S., and Parentani, R. (2000). How the Change in Horizon Area Drives Black Hole Evaporation. Nuclear Physics B, 575(1–2), 333–356. https://doi.org/10.1016/S0550-3213(00)00067-5.

Medved, A. J. M., and Vagenas, E. C. (2005). On Hawking Radiation as Tunneling with Logarithmic Corrections. Modern Physics Letters. Part A, 20(23), 1723–1728. https://doi.org/10.1142/S0217732305018025.

Medved, A. J. M., and Vagenas, E. C. (2005). On Hawking Radiation as Tunnelling with Back-Reaction. Modern Physics Letters. Part A, 20(32), 2449–2453. https://doi.org/10.1142/S021773230501861X.

Medved, A. J. M. (2002). Radiation via Tunneling in the Charged BTZ Black Hole. Classical and Quantum Gravity, 19(3), 589–598. https://doi.org/10.1088/0264-9381/19/3/313.

Medved, A. J. M. (2002). Radiation via Tunnelling from a de Sitter Cosmological Horizon. Physical Review. Part D, 66(12), 124009. https://doi.org/10.1103/PhysRevD.66.124009.

Padmanabhan, T. (2004). Entropy of horizons, Complexpath and Quantum Tunneling. Modern Physics Letters. Part A, 19(35), 2637–2643. https://doi.org/10.1142/S0217732304015257.

Parikh, M. K., and Wilczek, F. (2000). Hawking Radiation as Tunneling. Physical Review Letters, 85(24), 5042–5045. https://doi.org/10.1103/PhysRevLett.85.5042.

Parikh, M. K. (2004). Secret Tunnel Through the Horizon. International Journal of Modern Physics. Part D, 13, 2355–2359. https://doi.org/10.1142/S0218271804006498.

Parikh, M. K. (2002). New Coordinates for De Sitter Space and de Sitter Radiation. Physics Letters B, 546(3–4), 189–195. https://doi.org/10.1016/S0370-2693(02)02701-6.

Rahman, M. A., and Hossain, M. I. (2013). Hawking Non-Thermal and Thermal Radiations of Schwarzschild anti-de Sitter black hole by Hamilton–Jacobi method. Astrophysics and Space Science, 345(2), 325–330. https://doi.org/10.1007/s10509-013-1391-8.

Shankaranarayanan, S., Srinivasan, K., and Padmanabhan, T. (2001). Method of Complex Paths and General Covariance of Hawking Radiation. Modern Physics Letters. Part A, 16(9), 571–578. https://doi.org/10.1142/S0217732301003632.

Shankaranarayanan, S., Srinivasan, K., and Padmanabhan, T. (2002). Hawking Radiation in Different Coordinate Settings : Complex Paths Approach. Classical and Quantum Gravity, 19(10), 2671–2687. https://doi.org/10.1088/0264-9381/19/10/310.

Shankaranarayanan, S. (2003). [arXiv:grqc/0301090v2]. Temperature and Entropy of Schwarzschildde Sitter Space-Time. Physical Review. Part D, 67(8), 084026. https://doi.org/10.1103/PhysRevD.67.084026.

Srinivasan, K., and Padmanabhan, T. (1999). Particle Production and Complex Path Analysis. Physical Review. Part D, 60(2), 024007. https://doi.org/10.1103/PhysRevD.60.024007.

Vagenas, E. C. (2003). Generalization of the KKW Analysis for Black Hole Radiation. Physics Letters B, 559(1–2), 65–73. https://doi.org/10.1016/S0370-2693(03)00302-2.

Vagenas, E. C. (2002). Semiclassical Corrections to the Bekenstein-Hawking Entropy of the BTZ Black Hole Via Self-Gravitation. Physics Letters B, 533(3–4), 302–306. https://doi.org/10.1016/S0370-2693(02)01695-7.

Zhang, J. Y., and Zhao, Z. (2005). Hawking Radiation Via Tunneling from Kerr Black Holes. Modern Physics Letters. Part A, 20(22), 1673–1681. https://doi.org/10.1142/S0217732305017019.