INHOMOGENEOUS COSMOLOGICAL PERFECT FLUID MODELS IN MODIFIED THEORY OF GENERAL RELATIVITY WITH TIME DEPENDENT-TERM

R. N. Patra ¹

¹P.G. Department of Mathematics, Berhampur University, Odisha, India

		ABSTRACT
		The cosmological term is achieved with non-static inhomogeneous cosmological models when a perfect fluid generates the gravitational field's source. Einstein's field equations are solved for three physically significant examples (the vacuum cosmological model, the radiating cosmological model, and the Zeldevich model) using the gamma law equation of state.
Received 05 February 2023 Accepted 18 March 2023 Published 31 March 2023 Corresponding Author R. N. Patra, raghunathpatra09@gmail.com DOI 10.29121/ijetmr.v10.i3.2023.1314 Funding: This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors. Copyright: © 2023 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License. With the license CC-BY, authors retain the copyright, allowing anyone to download, reuse, re-print, modify, distribute, and/or copy their contribution. The work must be properly attributed to its author.
		Keywords: Inhomogeneous Cosmological Model, Perfect Fluid, Radiating Cosmological Model, Zeldevich Model

1. INTRODUCTION

Barber (1982) proposed his second self-creation theory of gravity, which modifies general relativity, in an effort to outperform Einstein's theory. The ideal fluid in this simplified theory of general relativity just splits the matter tensor as a reciprocal of the gravitational constant G, rather than gravitating directly. The local impacts shown in observational studies are predicted by this idea. Furthermore, by analysing the behaviour of photons and degenerate matter entities, this theory may be supported or denied. An accurate measurement of the deflection of light and radio waves passing near the sun, along with the discovery of anomalous precessions in pulsar orbits over central masses, would validate or invalidate such a notion. The theory predicts the perihelia of planets with the same precision as general relativity and in that regard; it is in agreement with observation to within 1%. In the limit .

In every way, this revised theory is similar to Einstein's theory. Many authors have examined the modified theory of general relativity from various perspectives. The Friedman-Barber field equations have been solved by Pimentel (1985) using the power law dependency of the scalar field on the scale factor as an assumption. In generalising Pimentel's work Pimentel (1985), Venkateswarlu & Reddy (1990), Soleng (1987) has obtained solutions for the vacuum-dominated, dust-filled universe of the flat FRW spase-time. Bianchi cosmological solutions of VIo type are found in the works of Reddy & Venkateswarlu (1989), both in vacuum and with perfect fluid pressure equivalent to the energy density. When the source of the gravitational field is a perfect fluid, Venkateswarlu & Reddy (1990) have also built spatially homogenous and anisotropic Bianchi type-1 cosmological macro models.

Space homogeneous and anisotropic Bianchi type-II and III cosmological models have been obtained by Shanthi & Rao (1991) in both vacuum and stiff fluid conditions. Carvalho (1996) obtained a homogenous and isotropic model of the primitive universe in which the gamma parameter of the "gamma law" state equation continually varies with cosmological time. He also presented a unified description of the primitive universe between the inflationary period and the epoch dominated by radiation. Shri Ram & Singh (1998) have obtained a spatially homogeneous and isotropic R-W model of the universe in the presence of perfect fluid by using the ‘gamma law” equation of state. Mohanty et al. (2000) have obtained vacuum and Zeldovich fluid models for plane symmetric anisotropic homogeneous space-time. Mohanty et al. (2002), Mohanty et al. (2003) have obtained an anisotropic homogeneous Bianchi Type-1 cosmological micro model in Barber’s second theory of gravitation wherein the scalar field describes the elementary particles and their interactions Srivastav & Sinha (1998). Also, they have obtained a micro and macro cosmological model in the presence of a massless scalar field interacted with perfect fluid. Panigrahi & Sahu (2003), Panigrahi & Sahu (2002), Panigrahi & Sahu (2003), Panigrahi & Sahu (2004) have obtained plane symmetric inhomogeneous macro models in Barber’s second theory of gravitation. Sahu and Bianchi Type-1 vacuum models have been obtained by Sahu & Panigrahi (2003). Sahu & Panigrahi (2006), Sahu et al. (2010) have investigated Masonic perfect fluid models in modified theory of general relativity.

The vitality energy tensor of matter, which is produced by a idealize liquid, is ordinarily the subject of examination for relativistic models. But to get more reasonable models, one must consider the consistency component in cosmology has pulled in the consideration of numerous analysts because it can account for tall entropy of the display universe Weinberg (1971), Weinberg (1972). The tall entropy by baryon and the momentous degree of isotropy of microwave infinite foundation radiation recommends that dissipative impacts in cosmology ought to be considered. Furthermore, it's over here. Thick impacts are anticipated to happen due to a few forms. These are the decoupling of neutrinos amid the radiation time and the decay of matter and radiation amid the recombination time Kolb & Turner (1990), gravitational string generation Turok (1988) and Barrow (1988) and molecule creation impact within the terrific unification time. Murphy (1973) illustrated that the presentation of bulk thickness can anticipate the peculiarity of the enormous bang. therefore, one would need to consider the nearness of fabric dissemination other than the idealize liquid to get practical cosmological models (see Gron (1990) for an audit of cosmological models with bulk consistency).

To our information none of the creators has examined the altered hypothesis of common relativity for plane symmetric inhomogeneous space time in nearness of idealize liquid with time subordinate term. In this paper, we have examined the consistency of this theory in the context of a perfect fluid.

2. Field Equations

Here we consider the space time portrayed by inhomogeneous metric of the frame

Equation 1

Where A, B are functions of ‘x’ and’ t’.

The field equations in Barbers second self-creation theory with time dependent cosmological constant are

Equation 2

Where , Equation 3

The vitality force tensor for idealize liquid is given by

Equation 4

Together with Equation 5

In commoving co-ordinate system the surviving components of the field equations (2)-(5) for the space time (1) are

Equation 6

Equation 7

Equation 8

Equation 9

Equation 10

Here after wards the prime (') and the subscript “4” denotes partial differentiation w.r.to x and t respectively.

In order to solve the field equations for obtaining solutions in explicit forms, we may consider different equation of state. As the metric potentials are functions of x and t, it is difficult to solve the field equations (6)-(10) for non-static case. Hence, we consider the following particular cases.

Case-1:

In this case the field equations (6)-(10) reduces to

Equation 11

Equation 12

Equation 13

Equation 14

Here we have the system of four equations in five unknowns. In order to make the system consistent, we take the help of gamma law equation of state

2.1. VACUUM MODEL

For this case equations (11)-(14) reduce to

Equation 15

Equation 16

Equation 17

. Equation 18

Using equation (16) in equation (15), we obtain

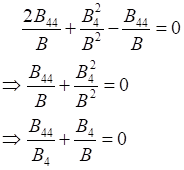
Equation 19

Integrating equation (19), we obtain

Equation 20

Where are constants of integration.

Now using equation (20) in equation (17) we get

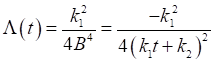Equation 21

For simplification if we consider is a function of ‘t’ only then equation (18) reduce to

Equation 22

With the help of equation (20), equation (22) reduces to

Integrating we get

Again integrating

Equation 23

Where are constants of integration.

If we consider is a function of ‘x’ only then equation (18) reduce to

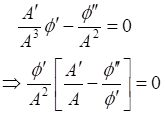
Equation 24

Integrating equation (2.4), we obtain

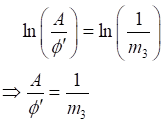
Equation 25

Again integrating equation (25), we get

Equation 26

Where and are constants of integration.

If we consider is a separable function of x and t and in the form of with zero separable constant then the Barbers scalar From equation (18) can be obtained as

Equation 27

Where is a constant of integration.

Further, if we are consider is a separable function of x and t and in the form of with zero separable constant, then Barbers scalar from equation (18),can be obtained as

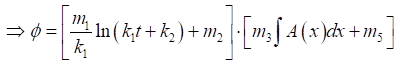. Equation 28

Hence the Vacuum cosmological model in second self creation theory of Barber can determined for any arbitrary metric potential.

2.2. Radiating Model:

In this case, equating equation (11) and (12), we find

Equation 29

On integration, equation (29) yields

Equation 30

where and are constants of integration. Now using (30) in equation (13), we obtain

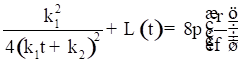
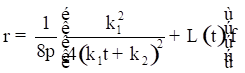. Equation 31

Further using equation (30) and in equation (14), we get

Equation 32

For the simplification, if we consider then equation (32) reduces to

Equation 33

This yield on intrgration

Equation 34

Where and are constants of integration.

If we consider, then equation (32) reduces to

Equation 35

Which on integration yields

Equation 36

Where and are constants of integration.

Using (34) and (36) in equation (31), we get

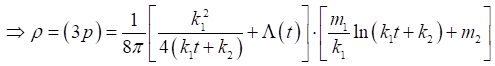Equation 37

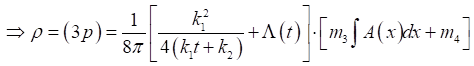Equation 38

Also, if is a separarable function of x and t and in the form of with zero separable constant then equation (32) yields

Equation 39

Where is a constant of integration.

Further, if we consider, then equation (32) yields

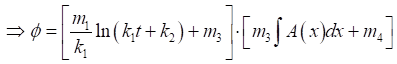Equation 40

Hence the radiating cosmological model in second self creation theory of Barber can be determined for any arbitrary metric potential.

Using (39) and (40) in equation (31), we can get another two values of

2.3. Zeldevich Model:

In this case the model doesn’t exist.

3. Conclusion

In this paper a plane symmetric inhomogeneous cosmological model has been constructed by taking perfect fluid along with time-depended cosmological constant term. Also, I have studied the consistency of this theory to the case of a perfect fluid in three different cases. The Vacuum and radiating cosmological model exists in second self creation theory of Barber and can be determined for any arbitrary metric potential, but in case of Zel’dovich model it doesn’t exist.

CONFLICT OF INTERESTS

None.

ACKNOWLEDGMENTS

None.

REFERENCES

Barber, G. A. (1982). On Two “Self-Creation” Cosmologies. Gen Relat Gravit 14, 117–136. https://doi.org/10.1007/BF0075691 .

Barrow, J. D. (1988). Nucl. Phys., B. 310, 743.

Carvalho, J. C. (1996). Unified Description of the Early Universe. Int J Theor Phys 35, 019–2028. https://doi.org/10.1007/BF02302426 .

Gron, O. (1990). Viscous Inflationary Universe Models. Astrophys Space Sci 173, 191– 225. https://doi.org/10.1007/BF00643930.

Kolb, E. W., & Turner, M.S. (1990). The Early Universe, Additson – Wesley, U.S.A.

Mohanty, G., Mishra, B., Das, R. (2000). Bull. Inst. Math. Academia Sinica, 28,43.

Mohanty, G., Panigrahi, U. & Sahu, R. (2002). Exact Bianchi Type-I Cosmological Micro-Model in Modified Theory of General Relativity. Astrophysics and Space Science, 281, 633–640. https://doi.org/10.1023/A:1015858621340 .