OPTIMIZATION OF SWITCHING ANGLES FOR SELECTIVE HARMONIC ELIMINATION IN CASCADED H-BRIDGE MULTILEVEL INVERTERS EMPLOYING ARTIFICIAL INTELLIGENCE TECHNIQUES – A MINI REVIEW

 

G Krithiga ¹, Mohan V ², Chitrakala G ³, Senthilkumar S ⁴

 

¹ Assistant Professor, Department of Electrical and Electronics Engineering, E.G.S. Pillay Engineering College, Nagapattinam, Tamilnadu, India

² Professor, Department of Electrical and Electronics Engineering, E.G.S. Pillay Engineering College, Nagapattinam, Tamilnadu, India

³ Principal, Freudenberg Training Centre, Nagapattinam, Tamilnadu, India

⁴ Assistant Professor, Department of Electronics and Communication Engineering, E.G.S. Pillay Engineering College, Nagapattinam, Tamilnadu, India

 

1. INTRODUCTION

The need of electrical energy is increasing day by day. Due to which, there is a depletion in conventional energy sources. Research has been carried out extensively to get the power from renewable energy sources Senthilkumar et al. (2022), Senthilkumar et al. (2014) and Mohan and Senthilkumar (2022). Among all the Renewable Energy Sources (RES), Solar and Wind energy have been chosen most commonly by all power electronics and power system research society irrespective of their environmental concerns Mohan et al. (2012). For gaining maximum power and also for enhancing the quality of power obtained from RES, it needs some power converter technologies which should be able to control and manage the power Bana et al. (2019). Normally the loads require ac power to operate. In turn, it clearly clarifies that the most important part of the renewable energy power conversion system is an Inverter Jeevananthan et al. (2021).

The output obtained from inverters contains harmonics. Therefore before giving this output to utility applications, it requires filters to remove the unwanted harmonics which in turn makes the whole system costly Mohan et al. (2012), Mohan et al. (2015), Mohan et al. (2017) and Chitrakala et al. (2017). In addition to that, high switching losses and high voltage stresses restricts the usage of that inverter in high power applications Sim et al. (2018). Particularly, the lower order harmonics should be eliminated from the output voltage of the inverter because of its undesirable effects.

The Multilevel inverter (MLI) have been used widely in the industry for medium voltage and high power applications owing to their advantages such as higher efficiency, lower switching losses and good electromagnetic compatibility than the two-level inverter Mohan et al. (2010) and Chitrakala et al. (2018) (2019). Due to the presence of several levels of dc voltages, the output waveform is synthesized to match the sinusoidal waveform Vadizadeh et al. (2013). To increase the performance and efficiency of the inverter, researchers have developed numerous modulation related control techniques.

We have discussed Neutral Point Clamped (NPC), Flying Capacitor (FC), Cascaded H-Bridge (CHB) MLIs in this paper. The Pulse Width Modulation (PWM), Space Vector PWM (SVPWM), Sinusoidal PWM (SPWM), phase shifted carrier PWM (PSC-PWM) and SHEPWM are the various modulation strategies Janardhan et al. (2020). Out of these, SHE PWM scheme has shown superior performance and control in eliminating the lower order harmonics from the inverter output voltage Konstantinou et al. (2013).

In SHEPWM technique, for finding the optimized Switching Angles (SAs), many complicated equations are involved to eliminate the unwanted harmonics in the inverter output voltage. Several numerical and algebraic methods like Newton Raphson (NR) method and Groebner bases theory are implemented in finding the solution to the complicated equations Krajčovič et al. (2018). These equations involve sine and cosine functions having different frequencies. For the above said methods, we have to assume some initial conditions to solve those equations. Suppose if the assumptions are wrong, then it will take much more iterations to converge to the optimum solutions Yang et al. (2015).

Different optimization techniques are used for solving the engineering problems particularly involving Artificial Intelligence (AI) techniques Baidoo (2017). The merits of these AI Algorithms are they are not completely depending upon the initial conditions, not complex, easily understandable, can implement in computers. The AI techniques are involved in many applications but their main role is in eliminating the harmonics from the output of the inverter Ab Wahab et al. (2015). AI Algorithms include Cuckoo Search algorithm (CSA), Shuffled Frog Leaping Algorithm (SFLA), Particle Swarm Optimization (PSO). The AI techniques performance mainly depends on the framing of objective function. By using this technique, we can reduce the objective function to get an optimized firing angle for eliminating the unwanted harmonics.

                                                                                                                                                  

2.  OVERVIEW OF MLI TOPOLOGIES AND MODULATION TECHNIQUES

2.1. MLI TOPOLOGIES

VSI’s are classified into two types: 1. Two-level inverter 2. MLI. Unipolar or Bipolar voltage waveforms are obtained from 2-level inverter. Staircase type waveform is obtained from MLI.

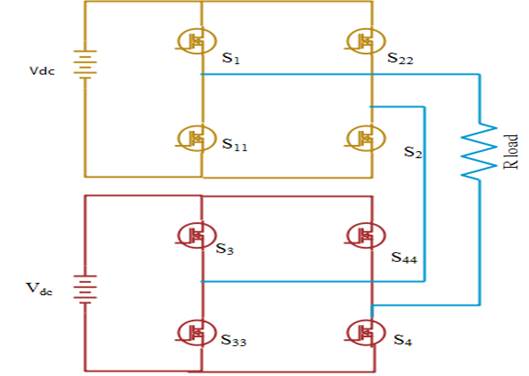
When compared to traditional 2-level inverter, the MLI uses high switching frequency pulse width modulation which makes it possible to applicable for high and medium power applications. The output voltage generated by the inverters will be increased when the numbers of levels increase Krithiga and Mohan (2022). The output waveform will be in the shape of staircase making a considerable reduction in Total Harmonic Distortion (THD). The basic topologies are NPC, FC and CHB. The schematic diagram of 5-level CHBMLI is given in Figure 2 and its switching pattern is given in Table 1.

Figure 1

                                                                     

Figure 1 Schematic Diagram of 5-Level Cascaded H-Bridge MLI

 

Table 1

Table 1 Switching pattern for 5-level Cascaded H-Bridge MLI
Voltage levels	S1	S11	S2	S22	S3	S33	S4	S44
2Vdc	ON	OFF	ON	OFF	ON	OFF	ON	OFF
Vdc	ON	OFF	ON	OFF	ON	OFF	OFF	ON
0	ON	OFF	OFF	ON	ON	OFF	OFF	ON
-Vdc	OFF	ON	OFF	ON	ON	OFF	OFF	ON
-2Vdc	OFF	ON	OFF	ON	OFF	ON	OFF	ON

 

For producing the Staircase output waveform, NPC and FC uses common dc source whereas the CHB uses a separate dc source. The CHB uses less number of components and also because of its modular and simple structure, it is most commonly used. A comparison of basic inverter topology is shown in Table 2.

Table 2

Table 2 Comparison of Basic Inverter Topology
Topology	Power Semiconductor Switches	Clamping Diodes per phase	DC bus capacitors	Balancing Capacitors per phase
Neutral Point clamped	2(m-1)	(m-1)(m-2)	(m-1)	0
Flying Capacitor	2(m-1)	0	(m-1)	(m-1)(m-2)/2
Cascaded H-Bridge	2(m-1)	0	(m-1)/2	0

 

2.2. SHEPWM TECHNIQUE

THD determines the output voltage quality of an inverter. Usually, the organizations have fixed some limiting values for THD Sivamani and Mohan (2022). Different methods have been implemented for improving the quality of an output voltage. 1. Fundamental switching frequency 2. High switching frequency. Among the two methods, the former can perform one or two commutations during one cycle of fundamental output voltage while the latter can do multiple commutations Bhatt and Chakravorthy (2015). The low cost and highly efficient energy conversion systems can be achieved by fundamental switching frequency techniques. The SHEPWM shows better performance in eliminating the lower order harmonics.

Some merits of SHEPWM:

Maximization of actual fundamental voltage along with minimization of lower order harmonics

Higher voltage gain can be obtained because of over modulation

SAs can be calculated priorly in many applications

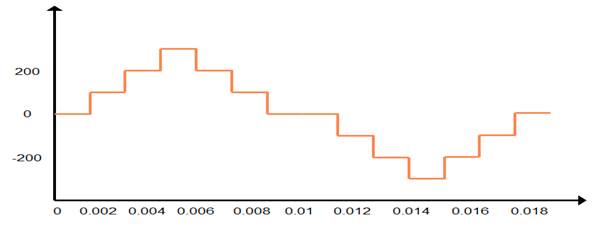
Figure 2

                                                                      

Figure 2 Simple Stepped or Type-A Output Waveform of CHBMLI

 

The type-A output waveform of CHBMLI is shown in Figure 2 and type-B output waveform is shown in Figure 3.

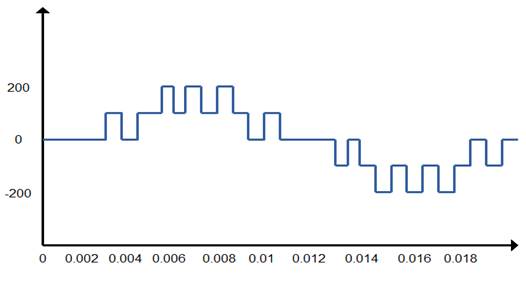
Figure 3

                                                                     

Figure 3 Notch Type (Type-B) Output Waveform Of CHBMLI

 

The Fourier series expansion can represent the output of CHBMLI for type-A waveform is given by

 

                                      Equation 1

 

since it is quarter wave symmetry, the Equation 1 can be modified as

 

                                                               Equation 2

 

The value of b_n can be written as (seven level inverter)

 

                                                       Equation 3

 

For eliminating the fifth and seventh harmonics, the output voltage is given by

 

            Equation 4

 

The non-linear transcendental equations of harmonics are given by

 

                           Equation 5

                                                                                 Equation 6

 

          Equation 7

 

The modulation index M is given by

 

                                                                                                                        Equation 8

 

Wherev₁ is the required fundamental voltage.

The Fourier series expansion can represent the output of CHBMLI for type-B waveform is given by

 

                                    Equation 9

 

Since it is quarter wave symmetry, the Equation 1 can be modified as

 

                             Equation 10

 

The simplified formula of b_n is

 

                                                                             Equation 11

 

where S is the number of H-bridges and M is the number of SAs per level. In SM number of SAs, we can eliminate SM-1 harmonics.

For a seven level inverter, 3H bridges are used and 3 SAs per quarter per step in a cycle which can eliminate possibly eight lower order harmonics 5^th, 7^th, 9^th, 11^th, 13^th, 15^th, 17^th, 19^th, 21^st and their corresponding equations are shown in                                                                                                              Equation 12,Equation 13, Equation 14, Equation 15, Equation 16, Equation 17, Equation 18.  In this, 9^th, 15^th, 21^{st are} third order harmonics, which can be eliminated from the three-phase system.

 

                                                                                                             Equation 12

 

                                                                                                    Equation 13

 

                                                                                      Equation 14

 

                                                        Equation 15

 

                                                      Equation 16

 

                                                      Equation 17

 

                                                                                 Equation 18

 

The above equations are non-linear transcendental equations which should be solved for finding the optimized SAs (α).

 

3. AI TECHNIQUES

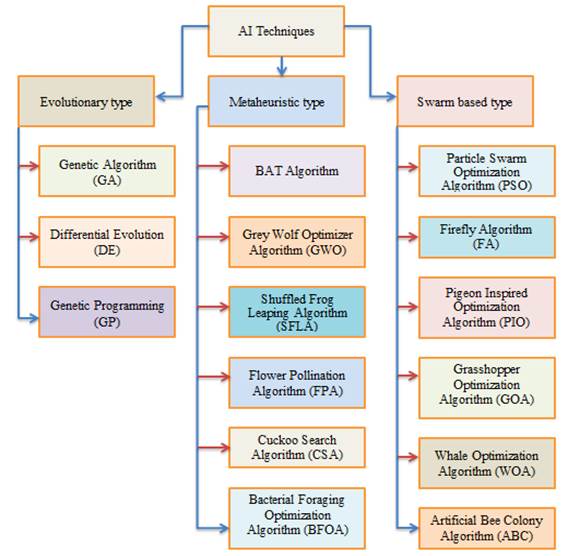
In this section, we discussed about various AI techniques involved in solving the non-linear transcendental equations of SHEPWM techniques to obtain the optimized SAs. The AI techniques discussed here are Differential Evolution (DE), Genetic Programming (GP), SFLA, Pigeon Inspired Optimization (PIO) Algorithm etc. Haamed and Hameed (2020). The types of AI techniques are shown in Figure 4.

 

3.1. SHUFFLED FROG LEAPING ALGORITHM (SFLA)

Siadatan et al. (2019) have discussed that like PSO, the SFLA shows comparatively better results than any other algorithms because of the usage of complicated search mechanism in finding the firing angles and also it requires minimum computation time.

 

3.2. PIGEON INSPIRED OPTIMIZATION (PIO) ALGORITHM

Mahesh and Sandhu (2018), Mahesh and Singh Sandhu (2019) discussed that the proposed algorithm requires only 6 iterations to reach the global optimum whereas GA requires 25 iterations that too it reaches only premature convergence stage. Based upon the results obtained, the proposed algorithm will be able to converge to global optimum solution within a very short span of time than any other algorithms.

 

3.3. FIREFLY ALGORITHM (FA)

Nawaz et al. (2013) estimated that the proposed algorithm minimizes the 5th harmonics but it cannot be minimized in GA and PSO Algorithms. This Algorithm gathers around the global optimum more quickly than other compared algorithms. Sundari et al. (2016) suggested a new method for estimating the optimum switching angle for cascaded multilevel inverter called Self-Adaptive Improved FA. They proved that the lower order harmonics namely 5th, 7th, 11th and 13th are eliminated well.

 

 

 

 

 

 

 

Figure 4

                                                                    

Figure 4 Types of AI Techniques

 

3.4. GRASSHOPPER OPTIMIZATION ALGORITHM (GOA)

Steczek et al. (2020) compared the proposed algorithm with PSO to reveal the highest probability of convergence. It also showed advantage over PSO particularly in the modulation index ranging between 0.5 and 1.

 

3.5. WHALE OPTIMIZATION ALGORITHM (WOA)

Dash et al. (2018) and Gharehchopogh and Gholizadeh (2019) concentrated on finding the best optimized SA for eliminating the lower order harmonics and also for reducing THD. The lower order harmonics (5^th, 7^th, 11^th and 13^th) are found to be less than 1% and up to 39^th harmonics it was less than 4.25%. It has the capability to escape from local minima.

 

3.6. GREY WOLF OPTIMIZER (GWO) ALGORITHM

Dzung et al. (2015) proposed to lower the selective harmonics as well as to reduce the overall THD value in the output of inverter. The result shows that the THD values of this method are comparatively lower than resultant and online step pulse PWM method. A comparison is made among GWO and modified GWO and the THD value of the latter has shown significant reduction Routray et al. (2020).

 

 

3.7. BAT ALGORITHM

Ganesan et al. (2015) investigated Bat optimization algorithm for solving the SHE problem. The simulated results are compared with the results of GA and BEE Algorithm and it is found to be satisfactory in eliminating the unwanted harmonics. Khamooshi and Moghani (2014)presented anexhaustive configuration for harmonic rejection and output voltage enhancement in multilevel inverters. They used two switching strategies, SHEPWM and optimal minimization of the total harmonic distortion and employed BAT algorithm for solving non-linear transcendental equations Stalin et al. (2022). They displayed the output obtained by two strategies.

 

3.8. FLOWER POLLINATION ALGORITHM (FPA)

Panda et al. (2020) proposed a new technique for evaluating the optimal angle to eliminate the predominant lower order harmonics from the output voltage. The experimental and simulated results justified the proposed method that it can track the optimal solution fast.

 

3.9. PARTICLE SWARM OPTIMIZATION (PSO)

Mohanty et al. (2018) formulated the objective function as to reduce THD using PSO Algorithm. With fewer steps, lesser number of equations and less computation time, it is achieved. Memon et al. (2018) presented selective harmonic elimination pulse width modulation technique-based hybrid Asynchronous PSO-NR (APSO-NR) algorithm for the eradication of unwanted harmonics in cascaded H-bridge multilevel inverter. The proposed algorithm can be applied to all levels of MLI having equal and unequal dc sources. In this paper, they combined the advantage of PSO and NR method and achieved global optimum value in lesser number of iterations.

 

3.10. GENETIC ALGORITHM (GA)

Hosseinzadeh et al. (2019) proposed a GA for eliminating the 3rd to 17th order harmonics in a 15-level cascaded H-bridge inverter. They found seven optimum switching angles. They obtained considerable reduction in THD value. Chatterjee et al. (2017) used genetic algorithm for solving the unconstrained equations of SHEPWM in order to attain the required firing angles thereby it could eliminate the odd harmonics existing in the output voltage of the inverter. The GA surmounts the limitation of the classical algorithm by forming a population of points instead of forming at each single point in every iteration Hameed and Kanbar (2019).

 

3.11. CUCKOO SEARCH ALGORITHM (CSA)

Singla (2019) developed a harmonic minimization function which optimizes the switching angles of a multilevel inverter. From the experimental and simulation results, it is found that the THD of the line voltage is measured as 7.9% using CSA optimization-based firing scheme whereas it is 25.3% using sinusoidal pulse width modulation firing scheme. Debnath (2012) proposed that the complexity in solving the tedious equations of SHEPWM can be solved using CSA thereby generating optimized switching angles. It completely eliminates or reduce the particular order harmonics in turn minimize the THD value.

 

 

3.12. Artificial Bee Colony (ABC) Algorithm

Yousef et al. (2018) showed that the ABC is capable of locating the optimum switching angles to generate perfect voltage. The proposed algorithm is evaluated with GA, PSO and BA and proved it is far advanced to others in all besides minimum cost function.

 

3.13. Bacterial Foraging Optimization Algorithm (BFOA)

Sultana et al. (2015) discussed that the main aim is to eliminate the dominant lower-order harmonics which is done by solving nonlinear transcendental equations, while maintaining the maximum fundamental component. BFOA is implemented to solve the aforesaid equations. It produced better results in the modulation indices of 0.7-0.8. The 5^th and 7^th harmonics are reduced considerably.

Table 3 shows the comparison of various AI techniquesand Table 4shows the various optimum switching angles obtained by implementing AI techniques in CHBMLI

Table 3

Table 3 Comparison of AI techniques
Techniques	Merits	Demerits	Applications
SFLA	simple concept, fewer parameter adjustments	low accuracy, time consuming, easily struck into the local optimum	effective in solving small to medium sized knapsack problems
PIO	very fast convergence rate	Easily struck into local optimum, low stability, and premature convergence.	continuous optimization problems
FA	gather around the optima more closely	parameter tuning, falling into local optima, low convergence speed	efficient in dealing with multimodal and global optimization problems
GOA	requires less effort	unstable convergence speed, easy to fall into the local optimum	micro grid applications, energy management, medicine, image processing, and financial issues
WOA	quick speed of convergence, ability to escape local minima.	not good at exploring the search space	content based image retrieval problem, multilevel thresholding segmentation, wind speed forecasting
GWO	simple algorithm, fewer adjusted parameters	Low accuracy, slow convergence, and poor local searching capability.	handling electromagnetic problems
BAT	simple, flexible, and easy to implement	converge very quickly at the early stage and then convergence rate slow down	image processing, continuous optimization in engineering Design
FPA	better solution, simple principle, few parameters, ease of operation	tendency towards premature convergence	sizing of distributed generation in distributed systems, engineering optimization problems, data fusion in wireless sensor networks
PSO	simple concept, robustness, implementation ease, few initial parameters	low convergence rate	used to solve non-linear, non-differentiable and multipeak optimization problems
GA	better solution	computation is complex, less accuracy	disease screening, diagnosis, software testing
CSA	easy to implement, less computation time, robust	easily falls into the local optimal solution, considerable delay in convergence	non-linear electrical problems
ABC	higher convergence, high accuracy	time consuming when it is applied to complex problems	neural network training, cluster analysis
BFOA	possibility of getting global optimum	struck into the local optimum	smart Grid, isolated micro-grid

 

Table 4

Table 4 Comparison of Optimum Switching Angles Obtained By Implementing AI Techniques In CHBMLI
AI used	level	MI	level or % harmonics				% THD
			H5	H7	H11	H13
SFLA	11	0.9	L	SH	NM	L	11.76
FA	11	0.81	L	L	L	H	9.04
I-FA	11	0.7	0.23	0.08	0.08	0.74	3.61
WOA	11	0.8	L	L	L	L	4.25
GWO	11	0.85	H	H	L	L	5
M- GWO	11	0.6	0.196	0.164	0.110	0.088	5.54
BAT	7	1.17	SL	M	L	H	18.65
PSO	11	0.66	L	H	L	L	6.6
Hybrid APSO	11	0.81	L	L	SH	H	8.56
GA	15	0.7	L	L	L	SH	3.12
CSA	7	1	L	L	L	SH	5.197
ABC	7	0.92	L	L	H	L	10.46
BFOA	7	0.8	0.61	0.87	NM	NM	11.71
L-Low, M-Medium H-High, SL-Slightly Low, SH-Slightly high, NM-Not mentioned

 

 

 

4. Scope for research

As discussed so far, SHEPWM technique is solved using different algorithms. When we are formulating a problem, it should be solved using at least 3 algorithms. Then only we could realize the efficacy of that particular algorithm. But it is not implemented in many papers.

It is clearly seen that there are many contradictions about the sovereignty of one algorithm over the other. In some references, the A algorithm is superior to B, and in some other references, A is inferior to B. In General, the performance of any algorithm is purely hinged on the application methods and tuning of their internal parameters. And also, the developing algorithm should have minimum parameters and also it should satisfy all requirements. So we need a new algorithm for eradicating the problems associated with harmonic elimination and also for reducing the THD value.

 

5. Conclusion

Eliminating harmonics in MLI is important since we are relying on RES. A review of AI techniques has been carried out for finding the optimized SA. The performance and limitations of 13 mentioned algorithms is presented. As per our discussion, we will develop a new algorithm to eliminate the harmonics and also for controlling the THD value.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Ab Wahab, M. N., Nefti-Meziani, S., and Atyabi, A. (2015). A Comprehensive Review of Swarm Optimization Algorithms. PLOS ONE, 10(5), 1–36. https://doi.org/10.1371/journal.pone.0122827.

Baidoo, E. (2017). Fireworks Algorithm For Unconstrained Function Optimization Problems. Applied Computer Science, 13(1), 61–74. https://doi.org/10.35784/acs-2017-06.

Bana, P. R., Panda, K. P., Naayagi, R. T., Siano, P., and Panda, G. (2019). Recently Developed Reduced Switch Multilevel Inverter For Renewable Energy Integration and Drives Application: Topologies, Comprehensive Analysis and Comparative Evaluation. IEEE Access, 7, 54888–54909. https://doi.org/10.1109/ACCESS.2019.2913447.

Bhatt, K., and Chakravorty, S. (2020). Mitigation of Harmonics From Output of Cascaded H Bridge Multilevel Inverter Using SHE PWM and AI Technique: A Review. Recent Advances In Electrical And Electronic Engineering, 13(7), 952–968. https://doi.org/10.2174/2213111607666200214121450.

Chatterjee, A., Rastogi, A., Rastogi, R., Saini, A., and Sahoo, S. K. (2017). Selective Harmonic Elimination of Cascaded H-Bridge Multilevel Inverter Using Genetic Algorithm. International Conference on Innovations In Power and Advanced Computing Technologies, 2017. https://doi.org/10.1109/IPACT.2017.8245005.

Chitrakala, G., Stalin, N., and Mohan, V. (2017). A Novel Programmed Low Frequency PWM Method For Performance Enhancement of Single-Phase To Single-Phase Cycloconverter. Ciit International Journal of Digital Image Processing, 9(2), 39–46.

Chitrakala, G., Stalin, N., and Mohan, V. (2018). A Segmented Ladder-Structured Multilevel Inverter For Switch Count Remission and Dual-Mode Savvy. Journal of Circuits, Systems and Computers, 27(14), 1850223. https://doi.org/10.1142/S0218126618502237.

Chitrakala, G., Stalin, N., and Mohan, V. (2020). Normally Bypassed Cascaded Sources Multilevel Inverter With RGA Optimization for Reduced Output Distortion and Formulaic Passive Filter Design. Journal of Circuits, Systems and Computers, 29(2), 2050019. https://doi.org/10.1142/S021812662050019X.

Debnath, R. (2012). Cuckoo Search: A New Optimization Algorithm for Harmonic Elimination in Multilevel Inverter. Journal of Bioinformatics and Intelligent Control., 11(1), 80–85. http://doi.org/10.1166/jbic.2012.1013

Dzung, P. Q., Tien, N. T., Dinh Tuyen, N., and Lee, H. (2015). Selective Harmonic Elimination For Cascaded Multilevel Inverters Using Grey Wolf Optimizer Algorithm. 9th International Conference on Power Electronics-ECCE Asia June 1 Convention Center, 5. Seoul. https://doi.org/10.1109/ICPE.2015.7168164.

Ganesan, K., Barathi, K., Chandrasekar, P., and Balaji, D. (2015). Selective Harmonic Elimination of Cascaded Multilevel Inverter Using BAT Algorithm. Procedia Technology, 21, 651–657. https://doi.org/10.1016/j.protcy.2015.10.078.

Gharehchopogh, F. S., and Gholizadeh, H. (2019). A Comprehensive Survey: Whale Optimization Algorithm and Its Applications. Swarm and Evolutionary Computation, 48, 1–24. https://doi.org/10.1016/j.swevo.2019.03.004.

Haamed, R., and Hameed, E. (2020). Controlling The Mean Arterial Pressure by Modified Model Reference Adaptive Controller Based on Two Optimization Algorithms. Applied Computer Science, 16(2), 53–67. https://doi.org/10.35784/acs-2020-12.

Hameed, W. M., and Kanbar, A. B. (2019). Using GA For Evolving Weights in Neural Networks. Applied Computer Science, 15(3), 21–33. https://doi.org/10.35784/acs-2019-18.

Hosseinzadeh, S. Salgueiro, Rivera, Wheeler. (2019). “Selective Harmonic Elimination in Cascaded H-Bridge Multilevel Inverter Using Genetic Algorithm Approach”. IEEE Publications. https://doi.org/10.1109/IPACT.2017.8245005.

Janardhan, K., Mittal, A., and Ojha, A. (2020). A Symmetrical Multilevel Inverter Topology With Minimal Switch Count and Total Harmonic Distortion. Journal of Circuits, Systems and Computers, 29(11), 2050174. https://doi.org/10.1142/S0218126620501741.

Jeevananthan, S., Chitrakala, G., Mohan, V., and Stalin, N. (2021). Inventive Optimization Tactics to Diminish Harmonic Distortion in Component Count Waned Normally Bypassed Cascaded Sources Multilevel Inverter. AU Patent, 2021101990.

Khamooshi, R., and Moghani, J. S. (2014). Comprehensive Harmonic Optimization in Cascaded H-Bridge Multilevel Inverters Using Variable DC Sources. The 5th Power Electronics, Drive Systems And Technologies Conference (PEDSTC 2014), Feb 5–6, 2014. Tehran. https://doi.org/10.1109/PEDSTC.2014.6799380.

Konstantinou, G. S., Ciobotaru, M., and Agelidis, V. G. (2013). Selective Harmonic Elimination Pulse-Width Modulation of Modular Multilevel Converters. IET Power Electronics, 6(1), 96–107. http://doi.org/10.1049/iet-pel.2012.0228.

Krajčovič, M., and Grznár, P. (2017). Utilisation of Evolution Algorithm in Production Layout Design. Applied Computer Science, 13(3), 5–18. https://doi.org/10.35784/acs-2017-17.

Krithiga, G., and Mohan, V. (2022). Elimination of Harmonics in Multilevel Inverter Using Multi-Group Marine Predator Algorithm-Based Enhanced RNN. International Transactions on Electrical Energy Systems, 2022, Article ID 8004425. https://doi.org/10.1155/2022/8004425.

Kumar Dash, S., Nayak, B., and Ballav Sahu, J. (2018). Selective Harmonic Elimination of an Eleven Level Inverter Using Whale Optimization Technique. International Journal of Power Electronics and Drive Systems (IJPEDS), 9(4), 1944–1951. https://doi.org/10.11591/ijpeds.v9.i4.pp1944-1951.

Mahesh, A., and Sandhu, K. S. (2018). Evolutionary Algorithm Based Optimal Angle Strategy For a Cascade H-Bridge Inverter. Procedia Computer Science, 125, 412–419. https://doi.org/10.1016/j.procs.2017.12.054.

Mahesh, A., and Singh Sandhu, K. (2019). Optimal Switching Angle Scheme For A Cascaded H Bridge Inverter Using Pigeon Inspired Optimization. International Journal of Emerging Electric Power Systems, 20(2). https://doi.org/10.1515/ijeeps-2017-0205.

Memon, M. A., Mekhilef, S., and Mubin, M. (2018). Selective Harmonic Elimination In Multilevel Inverter Using Hybrid APSO Algorithm. IET Power Electronics, 11(10), 1673–1680. https://doi.org/10.1049/iet-pel.2017.0486.

Mohan, V., Chitrakala, G., and Stalin, N. (2017). A Low Frequency PWM Based Multilevel DC-Link Inverter With Cascaded Sources. Asian Journal of Research In Social Sciences and Humanities, 7(1), 686–697. https://doi.org/10.5958/2249-7315.2016.01401.5.

Mohan, V., Jeevananthan, S., and Raja, J. (2012). An On-Line Adaptive Filtering For Selective Elimination of Dominant Harmonics from Line Currents of A VSI Fed Drive Using Recursive Least Square Algorithm. IEEE Publications – International Conference on Advances in Engineering Science and Management,773–778.

Mohan, V., Raja, J., and Jeevananthan, S. (2010). Frequency Domain Analysis of Adjustable Speed Drive Systems Based On Transfer Switching Function. Asian Power Electronic [Journal], 4(2), 64–68.

Mohan, V., Raja, J., and Jeevananthan, S. (2012). A Random PWM Scheme Based on Coalescing The Pseudorandom Triangular Carrier and The Randomized Pulse Position For Voltage Source Inverters, 4(11), 570–574.

Mohan, V., Stalin, N., and Jeevananthan, S. (2015). A Tactical Chaos Based PWM Technique For Distortion Restraint and Power Spectrum Shaping In Induction Motor Drives. International Journal of Power Electronics and Drive Systems, 5(3), 383–392.

Mohan, V., and Senthilkumar, S. (2022). Iot Based Fault Identification in Solar Photovoltaic Systems Using An Extreme Learning Machine Technique. Journal of Intelligent and Fuzzy Systems, 43(3), 3087–3100. https://doi.org/10.3233/JIFS-220012.

Mohanty, R., Chatterjee, D., and Sengupta, G. (2018). Design of PSO Based Cascaded Multilevel Inverter With Unequal DC Sources. International Journal of Engineering and Technology, 7(4). http://doi.org/10.14419/ijet.v7i4.38.24310.

Mousazadeh Mousavi, S. Y., Zabihi Laharami, M., Niknam Kumle, A., and Fathi, S. H. (2018). Application of ABC Algorithm For Selective Harmonic Elimination Switching Pattern of Cascade Multilevel Inverter With Unequal DC Sources. International Transactions on Electrical Energy Systems, 28(4). https://doi.org/10.1002/etep.2522.

Nawaz, F., Yaqoob, M., Ming, Z., and Ali, M. T. (2013). Low Order Harmonics Minimization in Multilevel Inverters Using Firefly Algorithm. IEEE Publications. https://doi.org/10.1109/APPEEC.2013.6837297.

Panda, K. P., Bana, P. R., and Panda, G. (2020). FPA Optimized Selective Harmonic Elimination in Symmetric–Asymmetric Reduced Switch Cascaded Multilevel Inverter. IEEE Transactions on Industry Applications, 56(3), 2862–2870. https://doi.org/10.1109/TIA.2020.2981601.

Routray, A., Singh, R. K., and Mahanty, R. (2020). Harmonic Reduction in Hybrid Cascaded Multilevel Inverter Using Modified Grey Wolf Optimization. IEEE Publications. 56(2), 1827-1838. https://doi.org/10.1109/TIA.2019.2957252.

Senthilkumar, S., Haidari, M., Devi, G., Francis Britto, A. S., Gorthi, R., Hemavathi, and Sivaramkrishnan, M. (2022). Wireless Bidirectional Power Transfer For E-Vehicle Charging System. International Conference on Edge Computing and Applications (ICECAA), 2022, 705–710. https://doi.org/10.1109/ICECAA55415.2022.9936175.

Senthilkumar, S., Mohan, V., Mangaiyarkarasi, S. P., and Karthikeyan. (2022). “M.Analysis of Single-Diode PV Model and Optimized MPPT Model For Different Environmental Conditions”. International Transactions on Electrical Energy Systems, 2022, 17.

Senthilkumar, S., Mohan, V., Senthil Kumar, T., Chitrakala, G., Ramachandran, L., and Devarajan, D. (2022). Solar Powered Pesticide Sprayer With Mobile Charger and LED Light. International Journal Of Innovative Science and Research Technology, 2022, 7(4).

Senthilkumar, S., Ramachandran, L., and Aarthi, R. S. (2014). Pick and Place of Robotic Vehicle By Using an Arm Based Solar Tracking System. International Journal of Advanced Engineering Research and Science, L(7), 39–43.

Siadatan, A., Fakhari, M., Taheri, B., and Sedaghat, M. (2019). New Fundamental Modulation Technique With SHE Using Shuffled Frog Leaping Algorithm For Multilevel Inverters. Springer.  

Sim, S. Y., Chia, C. K., Utomo, W. M., Goh, H. H., Buswig, Y. M. Y., Lim, A. J. M. S., Kek, S. L., Bohari, A. A., and Cham, C. L. (2018). Enhance Cascaded H-Bridge Multilevel Inverter With Artificial Intelligence Control. Indonesian Journal of Electrical Engineering and Computer Science, 11(1), 105–112. https://doi.org/10.11591/ijeecs.v11.i1.pp105-112.

Singla, S. P. R. (2019). Implementation of Cuckoo Search Optimized Firing Scheme In 5-Level Cascaded H-Bridge Multilevel Inverter For Power Quality Improvement. Journal of Power Electronics, 19(6), 1458–1466.

Sivamani, S., and Mohan, V. (2022). A Three-Phase Reduced Switch Count Multilevel Inverter Topology. International Transactions on Electrical Energy Systems, 2022. https://doi.org/10.1155/2022/6193731.

Stalin, N., Jeevananthan, S., Chitrakala, G., and Mohan, V. (2022). ‘A Bat Source String Succored Serrated H-Bridge Symmetrical MLI For Solar PV – Grid Integration’, AU [Patent], 2021104665.

Steczek, M., Jefimowski, W., and Szeląg, A. (2020). Application of Grasshopper Optimization Algorithm For Selective Harmonics Elimination in Low-Frequency Voltage Source Inverter. Energies, 13(23), 6426. https://doi.org/10.3390/en13236426.

Sultana, Sahoo, S. K., Prabhakar, S., Raglend, I., Chandrashekar, A., and Syampradeep, A. (2015). Application of Bacterial Foraging Optimization For Elimination of Lower Order Harmonics In Seven Level Inverter. Springer. http://doi.org/10.1007/978-81-322-2119-7_114.

Sundari, M., Rajaramb, M., and Sujatha. (2016). Application of Improved Firefly Algorithm For Programmed PWM In Multilevel Inverter With Adjustable DC Sources. Applied Soft Computing Journal, 41, 169–179. https://doi.org/10.1016/j.asoc.2015.12.036.

Vadizadeh, H., Farokhniah, N., Toodeji, H., and Kavousi, A. (2013). Formulation of Line-To-Line Voltage Total Harmonic Distortion of Two-Level Inverter With Low Switching Frequency. IET Power Electronics, 6(3), 561–571. https://doi.org/10.1049/IET-PEL.2012.0019.

Yang, K., Yuan, Z., Yuan, R., Yu, W., Yuan, J., and Wang, J. (2015). A Groebner Bases Theory Based Method For Selective Harmonic Elimination. IEEE Transactions on Power Electronics, 30(12), 6581–6592. https://doi.org/10.1109/TPEL.2014.2388077.