ON THE EXISTENCE OF UNIQUE COMMON FIXED POINT OF TWO MAPPINGS IN A METRIC-LIKE SPACE

 

Mainak Mitra ¹, Jigmi Dorjee Bhutia ²,  Kalishankar Tiwary ¹

 

¹ Department of Mathematics, Raiganj University, West Bengal, India

² Department of Mathematics, Kalimpong College, Kalimpong, West Bengal, India

 

1. INTRODUCTION

In 1922, Banach (1922) introced his result, known as Banach’s Fixed Point Theorem. After that several mathematicians worked on this result and made some successful attemps to generalize his idea in other ways. Recently in 2012, as a generalization of Banach’s Contraction Condition, Wardowski (2012) introduced a new type of contraction condition, called an -contraction. After this introduction, several mathemticians have widely used this idea to introduce some interesting results of fixed point. Beside these generalizations, some other mathematicians tried to generalize the notion of a Metric Space. Partial Metric Space Matthews (1994), Metric-Like Space Amini-Harandi (2012)are some notable generalizatons of the idea of a Metric Space. During these years several results on fixed point have been introduced on these spaces.

In our paper we’ll consider the Metric-Like Space and the -contraction to investigate the existence of a unique common fixed point for a pair of mapping. Foe that we’ll mention some definitions and results firts.

The idea of a Metric Space was introduced by M. Fréchet in the year 1906. Through this idea of Metric Space, he tried to define the distance between two points of an arbitrary set in an abstract manner as follows,

 

Definition 1.1 (Metric Space) Suppose  and  be a mapping such that 

1)    .

2)    .

3)    .

4)    .

 

then the mapping  will be called a Metric or a Distance Function on  and the ordered pair  will be called a Metric Space.

 

Example 1.2 The set  of all real numbers forms metric space with respect to metric , defined by .

 

Example 1.3 The set  of all complex numbers forms metric space with respect to metric ,defined by  , where  

 In 1994, S.G. Matthew introduced a generalization of metric space and referred it as a Partial Metric Space.

 

Definition 1.4 (Partial Metric Space) Matthews (1994) Suppose  and  be a mapping such that 

1)    ; .

2)     .

3)    ; .

4)    ; .

 

then the mapping  will be called a partial metric on  and the ordered pair  will be called a Partial Metric Space.

 

Example 1.5 In the set  of real numbers forms a partial metric space with respect to the mapping .

 

Example 1.6  In the set  of real numbers forms a partial metric space with respect to the mapping .

 In 2012, A.A. Harandi introduced a new generalization of metric space called a Metric-Like space

 

Definition 1.7 (Metric-Like Space) Amini-Harandi (2012) Suppose  and  be a mapping such that

 

1)    .

2)    .

3)    .

4)    .

 

then the ordered pair  will be called a Metric-Like Space or a Dislocated Metric Space.

 

Example 1.8  In the set  of real numbers forms a metric-like space with respect to the mapping .

 

Example 1.9  In the set  of real numbers forms a metric-like space with respect to the mapping .

 

Example 1.10 The set  of all real-valued continuous functions defined on a compact interval  forms a metric-like space with respect to te mapping .

 

Remark 1.11 Clearly every Metric Space is a Partial Metric Space as well as a Metric-Like Space. But 1.6, 1.8 shows that the converse is not true.

 

Remark 1.12 Every Partial Metric Space is a Metric-Like Space but 1.9 shows that the converse is not true.

 

Definition 1.13 (Convergence of a Sequence) Amini-Harandi (2012) In a metric-like space  suppose  be a sequence. Then  is said to converge to some limit  if  

 

Definition 1.14 (Cauchy Sequence and Completeness) Amini-Harandi (2012)

    1.  In a metric-like space  a sequence  is said to be a Cauchy Sequence if  exists finitely.

    2.  A metric-like space  is said to be a complete metric like space if for every Cauchy Sequence  in  there exists  such that .

 

Remark 1.15 In a metric-like space the limit of a sequence may not be unique. For example in the space  where  consider the sequence . Then for any real number , .

Remark 1.16 In a metric-like space a convergent sequence may not be a Cauchy sequence.

 

Remark 1.17 In a complete metric like space if a sequence  is a Cauchy sequence such that  then its limit will be unique. For this, suppose on the contrary that the limit of the sequence is not unique. Then there will exist  with the following properties

          

          

          

 Then    — a contradiction

The above fact leads to the following definition,

 

Definition 1.18 (0-Cauchy Sequence and 0-Complete Space) Shukla et al. (2013)

    • In a metric like space  a sequence  will be called a 0-Cauchy sequence if .

    • A metricclike space  is said to be a 0-Complete metric like space if every 0-Cauchy sequence in  converges to some point  such that .

 Clearly every 0-Cauchy sequence ia a Cauchy sequence and a complete metric like space is a 0-complete metric like space.

 

Definition 1.19 (Coincidence Point and Point of Coincidence) Jungck (1996)  Suppose  and  be two functions. A point  is said to be a point of coincidence of  and  if there exists  such that

          

The point  is called a coincidence point of  and .

 

Definition 1.20 (Weakly Compatible Mapping) Jungck (1996) Suppose  and  be two functions. Then  and  are said to be weakly compatible if they commutes at their coincidence points i.e. if , for some  then .

 In 2012, D. Wardowski introduced the idea of -contraction in the following manner;

 

Definition 1.21 (-Contraction) Wardowski (2012) Suppose,  be a mapping such that 

    1.   is strictly increasing.

    2.  .

    3.   such that .

 

The followings are some examples of such functions

Example 1.22  

Example 1.23   

Example 1.24.

 

  Now suppose  be a metric-like space and  be a mapping such that whenever ,  such that

          

then  is said to be an -contraction defined on .

Notations:

In our paper we’ll commonly use the folloing notations 

1)      satisfies the three conditons mentioned in Definition 1.21}

2)    For a mapping ,

3)    For mappings ,

4)    For mappings ,

 

2. SOME RESULTS

Lemma 2.1 Karapinar and Salimi (2013) In a metric-like space  the following results hold 

1)    .

2)    .

3)    If a sequence  converges to  such that , then for all   converges to .

4)    If  be a sequence in  such that  as , then  as .

5)    Suppose  be a sequence in  such that . If  then there exists  and two subsequences  and  of  such that the following sequences

will converge to  as  

 

Theorem 2.2 Amini-Harandi (2012) Suppose  be a complete metric-like space and  be a map such that  

          

 where  is a non-decreasing function such that 

1)    .

2)    .

3)    .

Then  has a fixed point.

 

Theorem 2.3 Amini-Harandi (2012) Suppose  be a complete metric-like space and  be a map such that  

          

where  is a non-decreasing continuous function such that . Then  has a unique fixed point.

 

Theorem 2.4 Karapinar and Salimi (2013) Suppose  be a complete metric-like space and  be a map such that  

          

where  is a non-decreasing function such that 

1)    .

2)    .

3)    .

If the range of  contains the range of  and  or  is a closed subset of X, then  and  will have a unique point of coincidence in X. Moreover if the mappings are weakly compatible, then they will have a unique common fixed point  such that .

For more fixed point results in a metric-like space we refer Amini-Harandi (2012), Karapinar and Salimi (2013), Shukla et al. (2013), Fabijano et al.(2020).

 

3. MAIN RESULT

We now introduce our main result;

Theorem 3.1 Suppose  be a 0-complete metric like space and  be two functions such that whenever  there exists  such that

 

                                                                     Equation 1

 

 for some . Then  and  will have a unique common fixed point in X.

 

Proof. Suppose  and define a sequence  as follows

 

          

          

          

          

          

 i.e. in general

 

          

 

Further let us denote by

 

          

 

Now let us consider the following cases

 

Case 1: Suppose  for some , then .

If  then,

 

Therefore  is a fixed point of .

Now if , then we have Equation 1 we have

 

                                                Equation 2

Where,

          
 

            

              

 

 Therefore from Equation 2 we have

 

          

 — a contradiction.

 

Hence  i.e.  is the fixed point of  and consequently the common fixed point of  and . If , then proceeding in the similar way we can prove that  and  will have a common fixed point.

Therefore if  for some  then  and  will have a common fixed point.

 

Case 2: Now let us assume that .

Then for  and  we have from Equation 1

 

                                                       Equation 3

Where,

             

 

 

 

 

 

 

 

 

 If , then Equation 3 will imply

                                               

                                                                                                                                                                                                                  Equation 4

—a contradiction.

Thus

          

          

          

Similarly, condsidering  and  in Equation 1 we can prove that

 

          

 

Therefore

 

          

 

Thus  is a monotonic decreasing sequence. Since it is bounded below by , it is convergent. Suppose the

 

          

.

Now if , then taking limit as  on both sides of (??) we have

 

          

 

— a contracdiction. Therefore

 

          

 

Now we claim that  is a 0-Cauchy Sequence i.e. . For this on the contrary, let us assume that  is not a 0-Cauchy Sequence. Then from Lemma 2.1 we have,  and two subsequences  of  such that the following sequences

          

          

 converges to .

Now if  and  are both even then taking  and  we have

 

          

 

Where, 

=

 

 

 

                         

 

 Taking  in the above inequality we have

 

          

 

— a contradiction as .

If  and  are both odd or one is even and other is odd then choosing suitable terms as  and  as above we will arrive at a contradiction.

This proves that  is a 0-Cauchy Sequence. Since  is a 0-complete metric like space, thus  is converges to  with .

 

Now if  then .

 

Since  is a 0-Cauchy sequence, thus uniqueness of limit implies that  does not converge to . Taking  and  in  Equation 1 we have

 

 Where, 

 

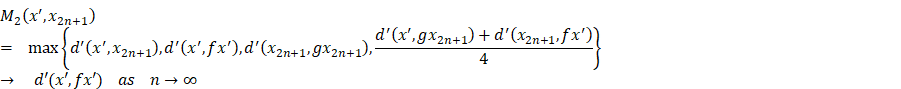
 Thus taking  in the above inequality we have

 

 — a contradiction.

Therefore

 

          

Thus  is a fixed point of .

Now if  then taking  in Equation 1 we have,

 where

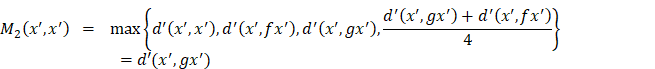
Therefore from the above inequality we have

 

          

 — a contradiction. Therefore

 

          

 

Thus  is a fixed point of .

Therefore  and  has a common fixed point.

 

Uniqueness:  To prove the uniqueness let us assume on the contrary that there exists two common fixed points  and  of  and . Then . Then taking  and  in  Equation 1 we have

 

 

 Where,

 

          

                             

 Therefore from the above inequality we have

 

 

 — a contradiction.

Thus

          

 

4. APPLICATIONS

The following results are the direct applications of the above theorem;

Theorem 4.1 Suppose  be a 0-complete metric like space and  be two functions such that whenever  there exists  such that

 

                                                               Equation 5

 

 Then  and  will have a unique common fixed point in X.

 

Proof. Considering  in Equation 1 we can have the following results.

 

Theorem 4.2 Suppose  be a 0-complete metric like space and  be two functions such that whenever  there exists  such that

 

                        Equation 6

 

 Then  and  will have a unique common fixed point in X.

Proof. Considering  in equation Equation 1 we can have the following results.

 

5. AUTHORS CONTRIBUTION

Conceptualization: M.Mitra, J.D. Bhutia.

Methodology: M.Mitra, J.D. Bhutia, K. Tiwary.

Formal Analysis: M.Mitra, J.D. Bhutia, K. Tiwary.

Investigation: M.Mitra, J.D. Bhutia;

Supervision:  K. Tiwary.

 

6. CONSENT OF STATEMENT

All authors have read and agreed to publish this manuscript.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Amini-Harandi, A. (2012). Metric-Like Spaces, Partial Metric Spaces and Fixed Points, Fixed Point Theory and Applications, 1(2012), 1-10. https://doi.org/10.1186/1687-1812-2012-204.

Banach, S. (1922). Sur Les Opérations Dans Les Ensembles Abstraits Et Leur Application Aux Equations Intégrales, Fundamenta Mathematicae, 3(1922), 133-181. https://doi.org/10.4064/fm-3-1-133-181.

Dhiman, D., Mishra, L.N. and Mishra, V.N. (2022). Solvability Of Some Non-Linear Functional Integral Equations Via Measures Of Noncompactness, Advanced Studies In Contemporary Mathematics, 32(2022), 157-171.

Fabiano, N., Nikolić, N., Fadail,,Z. M., Paunović, L. and Radenović, S. (2020). New Fixed Point Results on Αψl-Rational Contraction Mappings in Metric-Like Spaces, Filomat, 34(2020), 4627-4636.

Fabijano, N., Parvaneh, V., Mirkovic, D., Paunovic, L. and Radenovic, S.(2020). On F- Contraction of Jungck-Ciric-Wardowski-Type Mappings in Metric Spaces, Cogent Mathematics and Statistics , 7(2020). https://doi.org/10.1080/25742558.2020.1792699.

Jungck. G. (1996). Common Fixed Points For Noncontinuous Nonself Maps on Nonmetric Spaces.

Karapınar, E. and Salimi, P. (2013).Dislocated Metric Space to Metric Spaces With Some Fixed Point Theorems, Fixed Point Theory and Applications, 1(2013), 1-19. https://doi.org/10.1186/1687-1812-2013-222.

Matthews, S. G. (1994).  Partial Metric Topology, Annals of The New York Academy of Sciences, 728(1994), 183-197. https://doi.org/10.1111/j.1749-6632.1994.tb44144.x.

Mishra, L.N., Gupta, A. and Mishra, V.N. (2021). Application of N-Tupled Fixed Points of Contractive Type Operators for Ulam-Hyers Stability, Palestine Journal of Mathematics, 10(2021), 349-372.

Mishra, L.N., Raiz, M., Rathour, L., and Mishra, V.N. (2022).  Tauberian Theorems for Weighted Means of Double Sequences In Intuitionistic Fuzzy Normed Spaces, Yugoslav Journal of Operations Research, 32 (3), 377-388. https://doi.org/10.2298/YJOR210915005M.

Sanatee, A.G., Rathour, L., Mishra, V.N. and Dewangan, V. (2022). Some Fixed Point Theorems in Regular Modular Metric Spaces and Application to Caratheodory's Type Anti-Periodic Boundary Value Problem, The Journal Of Analysis. https://doi.org/10.1007/s41478-022-00469-z.

Shahi, P., Rathour, L., and Mishra, V.N (2022). Expansive Fixed Point Theorems for Tri-Similation Functions, The Journal of Engineering and Exact Sciences- Jcec, 8(2022), 14303-01e.

Sharma, N., Mishra, L.N., Mishra, V.N. and Pandey, S. (2020). Solution of Delay Differential Equation Via Nv1 Iteration Algorithm, European Journal of Pure and Applied Mathematics, 13(2020), 1110-1130. https://doi.org/10.29020/nybg.ejpam.v13i5.3756.

Shukla, S., Radenović, S. and Ćojbašić Rajić, V. (2013).  Some Common Fixed Point Theorems in 0-Σ-Complete Metric-Like Spaces, Vietnam Journal of Mathematics, 41(2013), 341-352. https://doi.org/10.1007/s10013-013-0028-0.

Tamilvanan, K., Mishra, L.N. and Mishra, V.N., and Loganathan, K. (2020). Fuzzy Stability Results of Additive Functional Equation in Different Approaches, Annals of Communications In Mathematuics, 3(2020), 208-217.

Wardowski, D. (2012). Fixed Points of a New Type of Contractive Mappings in Complete Metric Spaces, Fixed Point Theory and Applications, 1(2012), 1-6. https://doi.org/10.1186/1687-1812-2012-94.

Wardowski, D. and Dung, N.V. (2014). Fixed Points of F-Weak Contractions on Complete Metric Spaces, Demonstratio Mathematica, 47(2014), 146-155. https://doi.org/10.2478/dema-2014-0012.