An Efficient Compromised Imputation Method for Estimating Population Mean

 

Sandeep Mishra ¹

 

¹ Association of Indian Universities, New Delhi, India

 

1. INTRODUCTION

Imputation means replacing a missing value with another value based on a reasonable estimate. Information on the related auxiliary variable is generally used to recreate the missing values for completing datasets. Incomplete data is usually categorized into three different response mechanisms: Missing Completely at Random (MCAR); Missing at Random (MAR); and Missing Not at Random (MNAR or NMAR) Little and Rubin (2002). Missing completely at random (MCAR): Missing data are randomly distributed across the variable and unrelated to other variables. Missing at random (MAR): Missing data are not randomly distributed but they are accounted for by other observed variables. Missing not at random (MNAR): Missing data systematically differ from the observed values. From the above-mentioned classifications of missing data, we, in the present study, have assumed MCAR.

Auxiliary information is important for survey practitioner as it is utilized to improve the performance of the methods. It may be utilized at the design stage or the estimation stage of the survey to get the more efficient estimator. At estimation stage ratio, product and regression methods are traditionally used. Bhal and Tuteja (1991) introduced exponential ratio and product estimator for estimation of population mean. Many modifications have been proposed using these methods till date. For handling missing data on the study variable several extensions and developments were proposed in the literature. Singh (2003) suggested product estimation for imputation. Shakti Prasad (2018) adapts exponential product type estimator given by Bahal and Tuteja (1991) and proposed exponential estimators for imputation. Kadilar and Cingi (2008) investigated some ratio-type imputation methods and proposed three new estimators to overcome the problem of the missing data. Diana and Perri (2010) proposed three regression type estimators which were more efficient than the Kadilar and Cingi (2008). The present article suggests a general ratio product exponential type method of imputation and accordingly proposed three estimators using the different amount of available auxiliary information as utilized by Ahmad et al. (2006), Kadilar and Cingi (2008), and Diana and Perri (2010). The proposed methods are than compared by traditional procedure of imputation. The proposed estimators come out to be more efficient than the usual ratio, product, regression, and exponential method for handling missing observations to estimate the population mean.

Given a finite population , the objective is to estimate the population mean . A simple random sample wor, , of size  is drawn from the population . Let the responding units be  from the  sampled units. Let us denote  as the set of responding units and  the set of non-responding units, i.e.,  is observed for  but for units in  the values are not available and hence imputed values are derived by some method. In this paper we shall use the following notations:

: Population Size;  Sample size; : Number of responding units; : Population means of study variate  and auxiliary variate  respectively; :  Standard Deviation of study variate  and auxiliary variate  respectively; : Coefficient of variation of study variate  and auxiliary variate  respectively; : Correlation coefficient between  and ; .

 

2. Some existing methods of imputation

1)     The mean method of imputation suggests replacing the missing observations with the mean of the observations available on response units i.e.

 

Then the estimator of the population mean  is given by

 

                                    and its MSE is given by

 

 

 

                                                                                                       (1.1)

 

2)     The ratio method of imputation uses information on one auxiliary variable  and calculates the missing values by

Where

 

This gives the resulting estimator by

 

 

The MSE of  is given by

 

                                          (1.2)

 

It is noted that, in the presence of missing data, the availability of information on auxiliary variable  in the data set supports suggesting efficient estimators.

 

3)     Diana and Perri (2010) proposed three estimators as by using different regression-type method of imputation such that the imputed data is given by

 

 

 

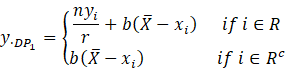
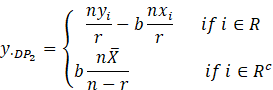
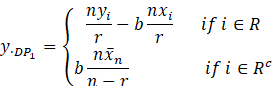
For these methods the resulting estimators are

 

 

 

                                                                (1.2)

 

                                                                                   (1.3)

 

                                                           (1.4)

 

They proved that the suggested estimators are more efficient than the Kadilar and Cingi (2008) estimators.  is always more efficient than both  and  , whereas  perform better than  if the condition

 

 

3. The proposed Estimator

The estimator suggested here is inspired by the Sahai (1985) estimator of population mean in case of simple random sampling, and is defined as

 

 

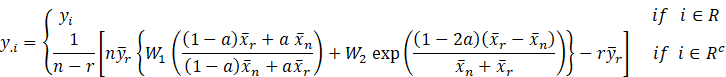
With the above imputation method, the resulting estimator of the population mean  is obtained as

 

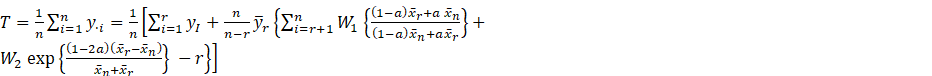                                                                                                          (2.1)

 

 and  are constant chosen suitably so that their choice minimizes the mean square error of the resultant estimator and   is a real constant. Our goal in this paper is to discuss the suggested estimators for different values of  and have a comparative study of the suggested estimator for these values of  in order to get the minimum MSE.

 

4. First Degree Approximation to the Bias

To derive the Bias and MSE expressions of the proposed estimator upto , we define

 

 

Thus, we have  

 

The expectation of these  are   

 

And under simple random sampling without replacement,

 

 

 

where ,   .

 

Now representing (2.1) in terms of ,  we have 

 

 

 

 

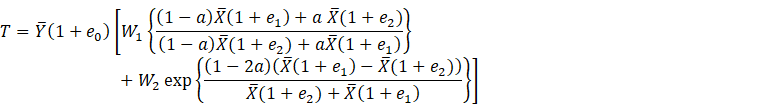
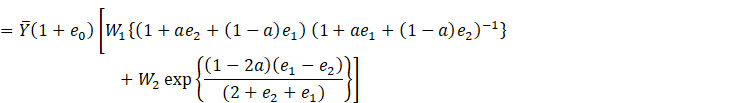
We assume that the sample is large enough to make  and  so small that contributions from powers of degree higher than two are negligible. By retaining powers up to  and , we get

 

 

 

 

 

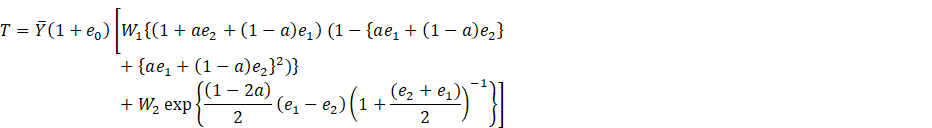
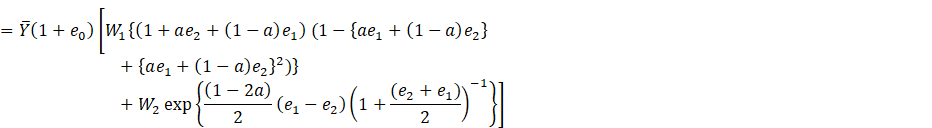
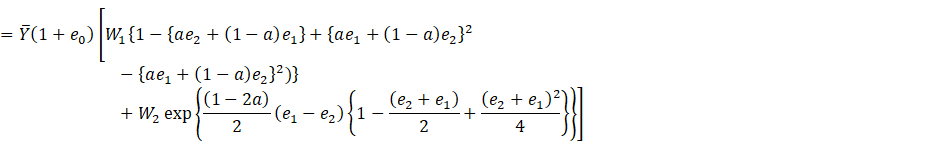
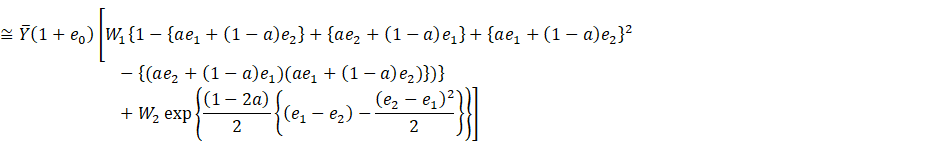
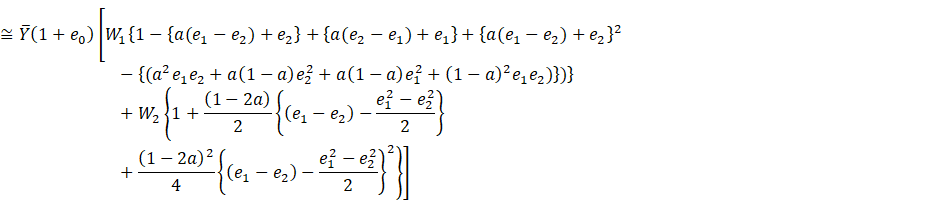
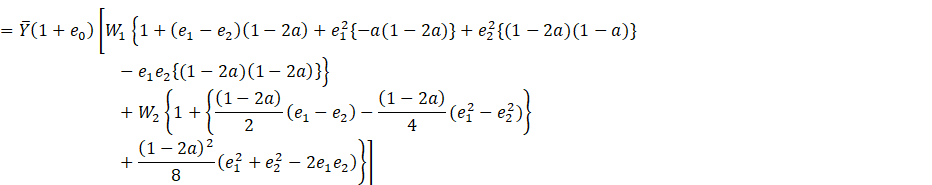
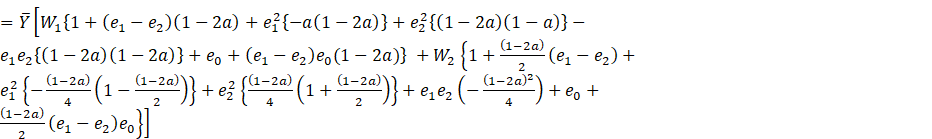                                                                                                                           (2.2)

 

Theorem 2.1.  The conditional bias up to the first order of approximation of the estimator  is given by the estimator is given as

 

 

Where  and

 

Proof: From (2.2) we have

 

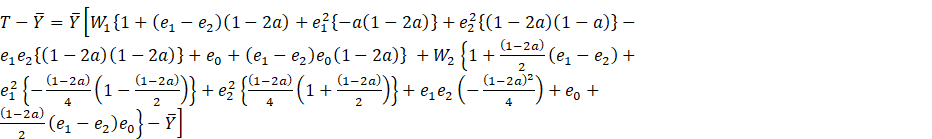                                                                                                               (2.3)

 

Taking expectation on both side we obtain the bias of  to order  as

 

 

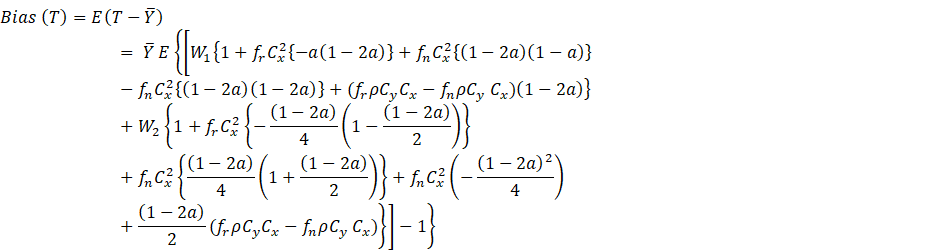
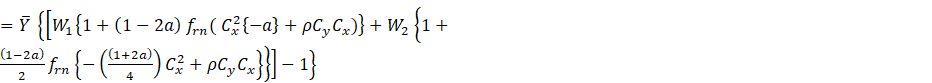                                                                            (2.4)

 

 Letting ,   in eq. (A.1)

 

 

5. Mean Squared Error of T

We calculate the mean squared error of  up to order   by squaring (2.2) and retaining terms up to squares in  and , and then taking the expectation. This yields the first-degree approximation of the MSE

 

Theorem 2.2. The minimum mean square error of the proposed estimator  is given by

 

 

The optimum values of  and   are:

 

 

 

 

Where
                                             
,                    

 

And the minimum MSE of the proposed estimator is given by

 

 

Proof:

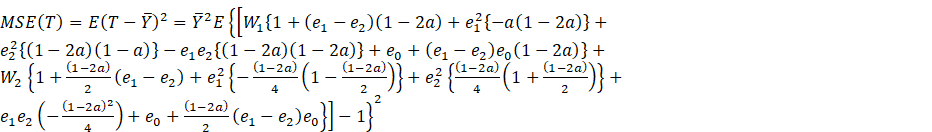                                                               (A.2)

 

Let coefficient of  and  in eq. (A.2) are  and  respectively then  is

                                                                                                                           (2.5)

 

Now, let

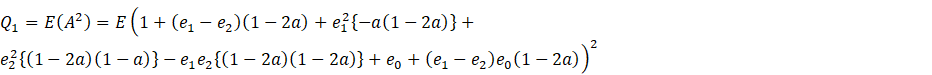
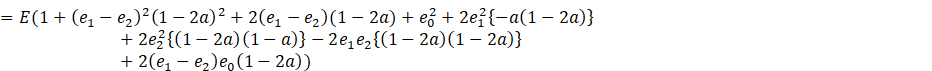
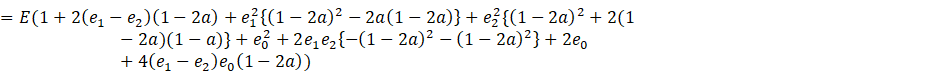
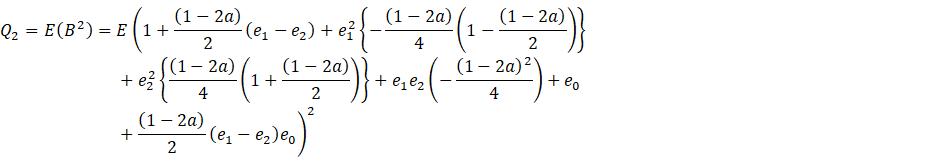
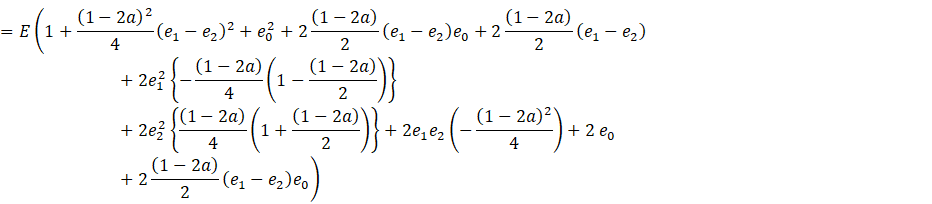
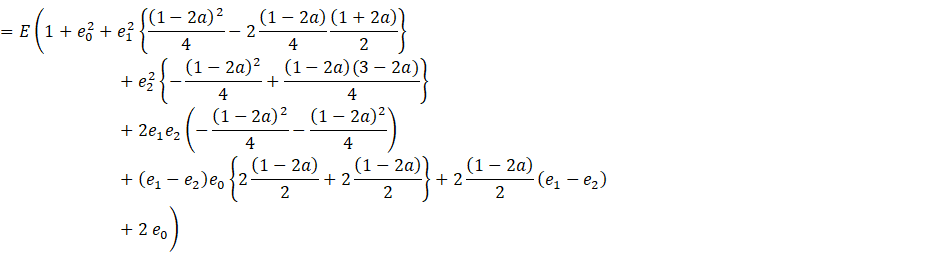
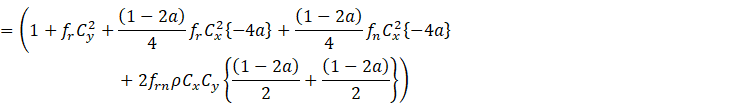
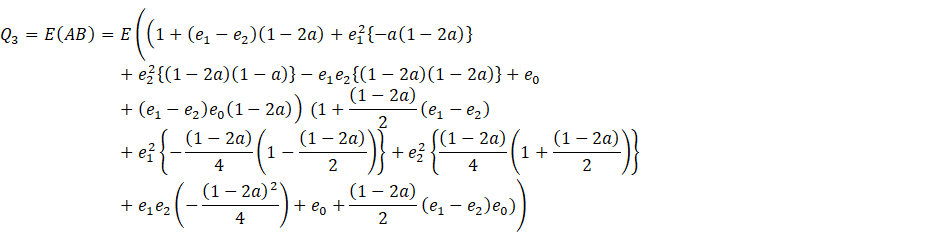
From previous theorem

,

 

Placing these values of   in (A.2) we get

 

 

 

Differentiating MSE with respect to  and , and equating to zero, we get

 

 

On solving these equations, we get

 

 

And after placing the values of  and  from () to the expression of MSE (?) the minimum MSE expression is

 

 

 

6. Expressions of MSE for different choices of

Here we consider the different forms of the proposed estimator for various values of .

 

Case 1.  

,                    

 

 

 

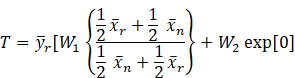
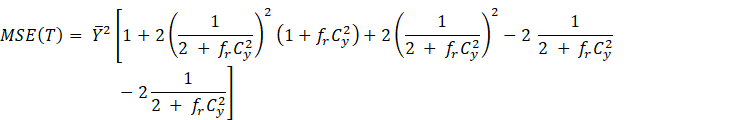
Which is better than the mean estimator  in terms of efficiency as

 

 

And if  ,  The proposed estimator at   is equivalent to the mean estimator

 

Case 2.   

                                             
,                    

 

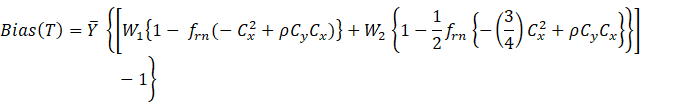
For

For

 

Case 3.   

 

A linear combination of product estimator and product type exponential estimator,

,  

 

                                             
,                    

 and further

For  it reduces to product estimator

 

and for it reduces to product type exponential estimator

 

7. Empirical Study

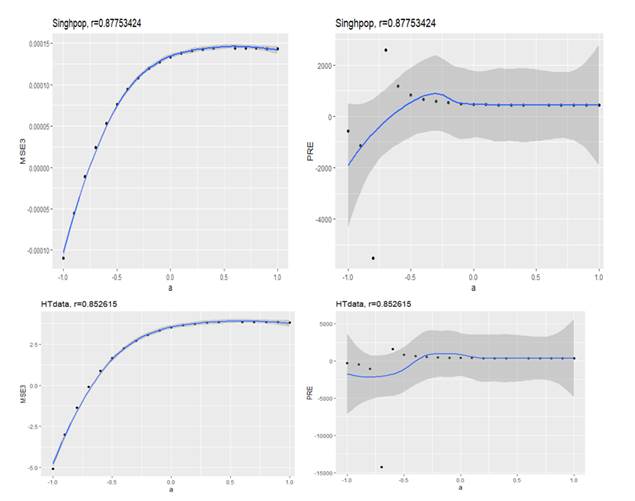
For the purpose of comparison of the proposed estimator we conducted the empirical study and computed the Percentage relative efficiency (PRE) of the estimators , , for (i) real data and (ii) artificially generated data.

The empirical study has been carried out to illustrate and compare the performance of the proposed imputation methods with the existing conventional imputation methods and the method proposed by Diana and Perri (2010) and Bhushan and Pandey (2010) utilizing Searl () constant with the Diana and Perri (2010) estimator for (i) real data described in Horvitz and Thompson (1952), Singh (2003), described in Table 1, Table 2.

Table 1

Table 1 Description of Populations considered for empirical study
Parameters	Population 1	Population 2
Description	Horvitz and Thompson (1952), : no. of houses on  th block. : eye estimate of no. of houses on  th block.	Singh (2003, pp 1114), the season-average price for commercial crop: season average price in $ per pound, by states,1994-96;  seasons average price per pound during 1996; : season average price per pound during 1995
	20	36
	7	18
	5	8
	21.15	0.2033
	19.7	0.1856
	94.028947	0.006458
	61.8	0.005654
	0.8526154	0.8775

 

The mean square errors (MSEs) and percent relative efficiencies (PREs) are calculated for the methods considered with respect to the mean method of imputation ( The methods

1)     Mean Method of imputation,

2)     Ratio Method of imputation,

3)     Diana and Perri method of imputation   

4)     Diana and Perri method of imputation   

5)     Diana and Perri method of imputation   

6)     Proposed method of imputation,

 

 

Table 2

Table 2 Mean square error and percent relative efficiency based on Population I(Singhpop)
Estimator		MSE	PRE	MSE	PRE
		0.000627874	100	14.1043421	100
		0.00029219	214.8858518	10.2000587	138.2771
		0.00048973	128.2082427	7.75712694	181.8243
		0.000144369	434.9080453	3.85114837	366.2373
		0.000282514	222.2456233	10.1983635	138.3001
		MSE and PRE of Proposed Estimator for different choices of
	-1	*-0.000109667	*-572.5264505	*-5.07540636	*-277.8958
	-0.9	*-5.54806E-05	*-1131.701446	*-2.98949277	*-471.7972
	-0.8	*-1.13765E-05	*-5519.055982	*-1.36603234	*-1032.5043
	-0.7	2.43566E-05	2577.844737	*-0.09897433	*-14250.5046
	-0.6	5.31303E-05	1181.763804	0.89001809	1584.7253
-0.5		7.61179E-05	824.8708681	1.66003196	849.6428
-0.4		9.4301E-05	665.8194857	2.25644120	625.0702
-0.3		0.000108506	578.656658	2.71463222	519.5673
-0.2		0.00011943	525.7257808	3.06257328	460.5389
-0.1		0.000127667	491.8054912	3.32262502	424.4939
0		0.000133722	469.5370246	3.51284069	401.5082
0.1		0.000138025	454.8999563	3.64791560	386.6411
0.2		0.000140943	445.4819583	3.73989064	377.1325
0.3		0.000142789	439.7214493	3.79868012	371.2959
0.4		0.00014383	436.5391782	3.83247219	368.0220
0.5		NaN	#VALUE!	NaN	-
0.6		0.000144359	434.9406963	3.85095252	366.2559
0.7		0.00014419	435.4483623	3.84580584	366.7461
0.8		0.000143911	436.2925635	3.83631355	367.6535
0.9		0.00014362	437.1774822	3.82543836	368.6987
1		0.000143389	437.8833031	3.81546698	369.6623

 

                                                                       

 

8. Interpretations of the computational results

The following interpretations may be read out from above Tables:

1)     For the real populations, HT data and Singh Population where the correlation between  and  is 0.852615 and 0.877534, the results are shown in Table 1. It is clear that the proposed imputation method  is superior to all the imputation methods i.e., and the imputation methods suggested by Diana and Perri  for a wide choice of the constant  for the proposed estimator.

 

CONFLICT OF INTERESTS

None. 

 

 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Heitjan, D.F. and Basu, S. (1996). Distinguishing 'Missing at Random' and 'Missing Completely at Random'. The American Statistician. 50(3), 207-213. https://doi.org/10.1080/00031305.1996.10474381.

Horvitz, D. G. and Thompson, D.J. (1952). A Generalization of Sampling Without Replacement From a Finite Universe. Journal of the American Statistical Association, 47(260), 663-685. https://doi.org/10.1080/01621459.1952.10483446.

Lee, H., Rancourt, E., and Sarndal, C.E. (1994). Experiments with Variance Estimation from Survey Data with Imputed Values. Journal of Official Statistics,10(3),231-243.

Rubin, R. B. (1978). Multiple Imputation for Nonresponse in Surveys. New York : John Wiley.

Singh, S. (2003). Advanced Sampling Theory with Applications. How Michael Selected Amy. Kluwer, Dordrecht, 1(2). https://doi.org/10.1007/978-94-007-0789-4.

Singh, S. and Horn, S. (2000). Compromised Imputation in Survey Sampling. Metrika, 51, 267-276. https://doi.org/10.1007/s001840000054.