DEVELOPMENT OF ONLINE LEARNING DEVICE WITH A CONTEXTUAL APPROACH TO IMPROVE STUDENTS' MATHEMATICS PROBLEM-SOLVING ABILITY

 

Dewa Ayu Krisna Apriyanti ¹ , I Gusti Putu Suharta ¹ ,  I Wayan Puja Astawa ¹

 

¹ Graduate Program, Mathematics Education, Ganesha University of Education, Indonesia

 

1. INTRODUCTION

Education is a form of embodiment of a dynamic human culture and full of development. Although education provides the possibility for students to get "opportunity," "hope," and knowledge to live, the more excellent the opportunity and hope dramatically depends on the quality of education taken Surya et al. (2017). Mathematics education aims to prepare students to use mathematics and mathematical thinking patterns in everyday life and in studying various sciences Suherman (2015). One of the abilities that students must possess is solving mathematical problems. Because by having these abilities, students can solve mathematical problems related to contextual or related to students' real lives.

Mathematical problem-solving ability is an ability that students must possess to solve a problem in mathematics, problems in other sciences, and problems in everyday life. However, this is not in line with the reality on the ground. When researchers conducted observations and interviews with mathematics teachers at the research school, namely SMPN 1 Gianyar, many students still had low mathematical problem-solving abilities. The researcher also pretested to determine the students' problem-solving abilities by giving two essay questions. The results showed that the students' problem-solving abilities were still low.

"The existence of mathematics learning device is necessary to support the implementation of learning" Sugiantara et al. (2013). Although based on the results of interviews with teachers, it was found that the learning device used, which included student worksheets and student books, only used printed books obtained from the government, the weakness of these learning device, according to the teacher, was that these devices were not enough to help improve students' problem-solving abilities.

There are still many students that are used today that emphasize the existing formula, not the process of its discovery. So that students will get used to something instant and memorized, while they will be less in understanding. This will be very unfortunate because it can reduce students' competence in reasoning or interpreting an existing problem, of course, it will significantly affect the mental development and mindset of students in the future, and it will also reduce the meaning of a mathematics lesson. Furthermore, the worksheets and student books do not provide opportunities for students to build their knowledge and be active in class. One suitable approach to developing learning device is contextual, and this approach has seven main components of learning Muslich (2007). Learning with a contextual approach is a learning concept in which the teacher brings real-world situations into the classroom and encourages students to make connections between their knowledge and apply it in their lives.

This research is also motivated by previous studies. One of them is research conducted by Barata (2015) which finds that learning device with a contextual approach to comparative material get products in the form of valid, practical, and influential Student Books and Worksheets. This study found that the components of social interaction, student activity in constructing and discovering knowledge in student books, and worksheets were still not fully implemented. For the reaction principal component, the teacher aroused student motivation and created a comfortable atmosphere for learning that had not been appropriately implemented. Agriat Barata research suggests that teachers should relate subject content to real-world situations and motivate students to make connections between knowledge and its application in everyday life. Therefore, this study again raises the contextual approach and corrects the weaknesses in Barata (2015)research.

Another study, namely research by Aminah and Irawati (2018), obtained the results of a learning device with a contextual approach to valid cube and block material. The obstacle in the research was regarding the students' mistakes in using the formula for surface area and volume of cubes and blocks. In these questions, students are required to write and calculate story problems related to formulas for surface area and volume of cubes and blocks. Therefore, the learning device that will be made in this study will make students better understand the use of volume and surface area formulas, in this case, in the material of curved sides, especially in story problems. Another research that encourages this research is from Makmuri et al. (2021), which develops an android-based mathematics learning application with a contextual approach to straight-line equation material for class VIII students who get decent results as a source of learning mathematics. The research only develops learning media without its implementation and evaluation. Therefore, this research develops a device that not only produces media in the form of applications but also implements and evaluates them in the form of student math problem-solving tests with more evident application operating instructions.

Another thing that was obtained after observations and interviews with teachers and class IX students at SMPN 1 Gianyar was that the use of technology was still lacking in learning even though, in the current era of globalization, technology was needed would be very helpful in teaching and learning activities. Keengwe & Georgina conveyed that there was a change in the implementation of teaching and learning caused by the development of technology Keengwe and Georgina (2012). Not to mention the consequences of the COVID-19 pandemic causing learning in schools to be carried out online, so it is important to utilize technology in lessons, one of which is the use of learning devices. Taking into account these conditions, it is necessary to develop an online learning device that can improve students' mathematical problem-solving abilities.

The material developed in this research is geometric, namely the curved side space. The reason for choosing this material is because, based on the results of interviews with mathematics teachers, it is said that students have difficulty solving problems in the curved side shape material, there are still obstacles and errors that students encounter when solving problems in the curved side building material. The results of research by Nuraida (2017) and Arifin et al. (2017) show that students experience obstacles in organizing data, sorting, using symbols, mathematical manipulation, procedural understanding, and drawing conclusions. Meanwhile, Entyka and Riyadi (2016) stated that mistakes made by students in solving problems of curved side space often occur during the process of understanding questions, developing strategies, implementing strategies, or re-examining the results of their work.

 

2. MATERIALS AND METHODS

This type of research is design research. Design research is a renewal of development research and emphasizes that design research is oriented towards developing theories or products that can be used to solve fundamental educational problems. The object of this research is an online learning device using a contextual approach to improve the mathematical problem-solving abilities of Class IX Middle School students. The subjects in this study were class IX students of SMP Negeri 1 Gianyar, especially class IX A, as many as 41 students in the field trial I, class IX B, as many as 42 students in the field trial II, and class IX C as many as 20 people who were selected-randomized in a limited trial. The research was carried out in the even semester of the 2021/2022 academic year. According to Plomp (2007), the phases of design research of the type of development study consist of preliminary research, prototyping, and assessment. The product development process or prototype can be seen in the following diagram: Figure 1

 

 

 

 

 

Figure 1

                                                                      

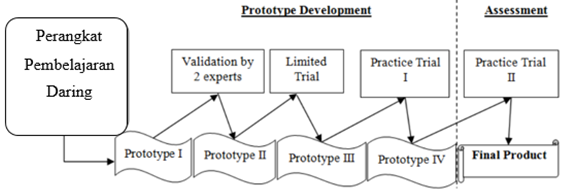
Figure 1 Product Development Process

 

The research instrument as a means of collecting research data consists of:

The instrument to measure the validity of the learning device is a validation sheet, this instrument is used to obtain data from the validators (2 experts). The information obtained is used as material for improving learning device that have been developed so that later they produce valid products. The validation results are recapitulated to determine the average validation score and determine the category of scores obtained. In determining the category of scores obtained, the following validity criteria are used: Table 1

Table 1

Table 1 Validity Criteria
No	Score	Criteria
1	3.5 Sr < 4.0	very valid/very practical
2	2.5 Sr < 3.5	valid/practical
3	1.5 Sr < 2.5	invalid/impractical
4	1.0 Sr < 1.5	very invalid/very impractical

 

The instrument to measure practicality is the practicality sheet. The sheet is in the form of a questionnaire/questionnaire, namely a teacher response questionnaire, a student response questionnaire, and a learning device implementation sheet. The results of the contents are analysed to determine category scores using the following practicality criteria. Table 2

Table 2

Table 2 Practical Criteria for Learning Device
No	Achievement rate (%)	Category
1.		Very Practical
2.		Practical
3.		Practical enough
4.		Less Practical
5.		Not Practical

 

According to the material in the learning device developed in this study. Learning devices are said to be effective if the average score of students' mathematical problem solving the concept test reaches the learning standart minimum set by the school, which is 85. The rubric for scoring or finding students' mathematical problem-solving scores in this study uses an analytical scoring rubric for each item, detailed in the following Table 3:

Table 3    

Table 3 Mathematical Problem-Solving Ability Scoring Rubric
Indicator	Score	Criteria
Understanding the problem	3	Rewrite the known and asked information correctly.
	2	Rewrite information that is known and asked but is not clear.
	1	Rewrite information that is known and asked but is incorrect.
	0	Do not rewrite information that is known and asked.
Make a problem-solving plan	3	Make pictures / sketches / graphs / tables and theorems / rules / theorems completely and both are correct.
	2	Make pictures/sketches/graphs/tables but it's still wrong while the arguments/rules/theorem true or vice versa.
	1	Make pictures/sketches/graphs/tables and propositions/rules/theorems but both are wrong.
	0	Do not make pictures / sketches / graphics / tables / symbols and propositions / rules / theorems
Solve the problem	3	Perform calculations according to the correct plan and get the correct results.
	2	Perform calculations according to the correct plan but the results are wrong.
	1	Perform calculations not according to the correct plan.
	0	Does not perform calculations.
Check back	1	Checking the process and answers and drawing conclusions properly and correctly.
	0	Not checking the process and answers and drawing conclusions but still wrong or not drawing conclusions.                                                                                Parwati et al. (2018)

              

3. RESULTS AND DISCUSSIONS

The first phase carried out in the research is preliminary research. In this phase, activities are carried out in the form of preliminary analysis of problem identification to obtain data regarding field needs in order to improve the quality of learning mathematics in the classroom. In the preliminary research phase, researchers began to develop online learning device using a contextual approach. The results of the preliminary analysis carried out obtained some information related to students' problem solving abilities and the state of the learning process in the classroom. The information was obtained by conducting interviews with teachers, providing questionnaires and problem-solving questions for students as well as classroom observations. Information obtained from interviews with teachers, namely the ability of students to understand mathematical concepts is quite good, but in solving story problems related to everyday life it is still not good enough. Moreover, if given unusual questions, they will find it difficult to solve them. This is caused by the habit of students working on routine questions taken from textbooks, so they are not accustomed to solving non-routine questions.

Based on the results of observations in class, the learning process has followed the learning method recommended in the 2013 curriculum, but its implementation has not been maximized. The teacher explains the material and then provides exercises that are in accordance with the examples. The teacher has carried out learning in accordance with the lesson plans used, but the lesson plans can still be developed again to help improve students' problem solving abilities. The teaching materials used, namely student worksheets, are still in the form of a collection of exercises, are static, do not cover all competencies and generally are not the work of the educator concerned.

The results of the problem-solving ability test given to students, it was found that many students who worked on the questions did not match the problem-solving indicators. This shows that students have not been able to solve the problems of problem solving skills well. At the stage of curriculum analysis, a review of the 2013 Curriculum was carried out for mathematics subjects for class IX SMP. Analyzing the curriculum aims to find out whether the material being taught is in accordance with the expected competencies. Curriculum analysis is focused on the analysis of KI and KD. Curriculum analysis aims as a guide in developing learning device with a contextual approach for grade IX students of SMP. The results of the KI and KD analysis contained in the content standard are translated into indicators of learning achievement.

Prototyping phase, in this phase, the learning device that have been produced in the preliminary research phase (called prototypes) are seen for their quality or feasibility as learning device. The resulting prototype is still in the form of prototype I which includes lesson plans, student books, student worksheets, and math problem solving tests which then need to be tested for validity, practicality, and effectiveness. The prototype I that had been produced was then validated by several experts, in this case one lecturer of the Master of Educational Technology Study Program, Ganesha University of Education and one mathematics teacher at SMP Negeri 1 Gianyar. Prototype I which has been validated and declared fit for use is then revised according to the advice of the experts. The result of the revision is referred to as prototype II, which is a prototype that is ready to be tested at the school where the research is located. The results of the assessment analysis by validators for online learning device including lesson plans, student books, student worksheets, and student math problem solving tests are shown in Table 4 below.

Table 4

Table 4 Summary of Learning Device Assessment Results from Validators
No	Learning Media	Average score		Average	Category
		Validator I	Validator II
1	Lesson Plans	3.76	3.86	3.81	Very Valid
2	Student Book	3, 88	3.81	3.84	Very Valid
3	Student Worksheets	3, 86	3.86	3.86	Very Valid
4	Problem-Solving Test				Valid

 

 

 

 

Figure 2

                                                                      

Figure 2 Display of Student Worksheets and Student Books

 

The first trial is a limited trial. This trial was conducted with several students in class XI C as many as 20 randomly selected students. The main purpose of this trial is to get an overview of the implementation of the developed learning device. In addition, at the limited trial stage, a response questionnaire was distributed to students and to teachers to determine the practicality of the learning device developed. All forms of revision obtained from this limited trial are used to revise prototype I until the revised result is called prototype III. In this trial, several obstacles were found in learning mathematics, among others, teachers and students still did not understand how to operate the application so that it took time to explain to students the things they asked, causing the time allocation that had been made in the lesson plan did not match what happened in the lesson plan.

Furthermore, prototype III which has been compiled based on revisions is then retested. The next trial is called field trial I. The focus of this trial is to improve product quality in terms of effectiveness and practicality. Field trial I was carried out on 41 students of class IX A. Observations and the provision of response questionnaires were carried out to see the implementation and practicality of the learning devices. All the results from the field test I were used as material to revise the prototype III. The results of the repair of prototype III hereinafter referred to as prototype IV. At the field trial stage I the teacher already understood how to operate the application so that it was easier to explain to students and made it easier for students to understand the operation of the application.

Finally, the assessment phase was carried out , where a field test was carried out using prototype IV by involving students in different classes, namely class IX B students, which consisted of 42 people. Observations and the provision of response questionnaires were carried out to see the implementation and practicality of the learning devices. Based on the results of the second field trial, it was found that the learning device had met the criteria of practicality and effectiveness so that all forms of improvement were used as revision material and in the end the final product was obtained. The summary of the results of the analysis of the implementation of learning device, student response questionnaire data, teacher response questionnaire data to see the practicality of learning device and the results of math problem solving tests to see the effectiveness of learning device can be seen in Table 5, Table 6, Table 7, Table 8 below:

 

 

 

Table 5

Table 5 Summary of Results of Analysis of Learning Device Implementation Sheet
Trials	Average Score (Sr)		Total	Sr. Total	Information
	Observer I	Observer II
Limited	2.76	2.88	5.64	2.82	Practical
Field I	3.22	3.22	6.54	3.27	Practical
Field II	3.35	3.32	6.66	3.33	Practical

 

Table 6

Table 6 Summary of Student Response Questionnaire Data Analysis Results
Trials	Practicality Value (%)	Category
Limited	80.4	Practical
Field I	81.27	Practical
Field II	83.52	Practical

 

Table 7

Table 7 Summary of Teacher Response Questionnaire Data Analysis Results
Trials	Practicality Value (%)	Category
Limited	84	Practical
Field I	88	Practical
Field II	90	Very Practical

 

Table 8

Table 8 Summary of Student Mathematics Problem-Solving Test Results
Trials	Average Score	Criteria
Field I	90.24	Complete
Field II	93.45	Complete

 

Concerning the quality of learning device, the average score of the validity of learning device, including lesson plans, student books, and student worksheets, is 3,81, 3,84, and 3,86, respectively. The three scores are very valid criteria, so the learning device were developed to meet the valid criteria. This learning device is also said to be practical because the learning implementation sheet shows a score of 2.82 in the limited trial, 3.27 in the field trial I, and 3.33 in the field test II, where all three are categorized as Practical. The practical value of student responses to the implementation of learning device in the limited trial, field trial I, and field test II were 80.4 %, 81.27%, and 83.52%, respectively. The three practical values are included in the practical category. The value of practicality for the teacher's response questionnaire on the implementation of learning device in the limited trial implementation shows 84%, including practical criteria.

Meanwhile, the value of practicality based on the teacher's questionnaire response to learning device in the field test I and field test II respectively, showed 88%, which was included in the practical category and 90% in the very practical category. Suppose you look at the results of the three practical instruments. In that case, the practicality of the limited trial stage to the second field trial stage has increased because, in the limited trial stage, students and teachers still have difficulty operating the application, maybe because this is something new for students. They learn to use the application, but after the teacher understands how to handle it better, the teacher can better explain or answer student questions regarding how to operate the application properly. Based on the result data obtained from the implementation sheet, student response questionnaire, and teacher response questionnaire, it was found that the learning device developed met the practicality criteria.

The learning device developed can meet the effectiveness criteria. This is indicated by the average math problem-solving test scores of students in grades IX A and IX B are 90.24 and 93.45, respectively. Both scores meet the established effectiveness criteria, above the specified learning standart minimum, which is 85. Furthermore, when viewed from the results of students' answers to the problem-solving test, almost all students have answered the test according to the indicators or problem-solving steps; it's just that many students make mistakes in the calculations. And change the units in the answer as requested by the question.

After the end of the study, interviews were conducted with several students related to the implementation of learning, the results showed that they felt learning using the Math in Dimension application was more interesting than using only the student worksheets obtained at school, the questions used in the student worksheets and student books using questions. Stories and being close to them also make it easier for them to understand the material and solve the given mathematical problems. They also suggested that an application be made that can not only be installed on Android but also iOS and desktops so that those who do not have Android can also install it on their respective gadgets without having to borrow from friends who use Android.

In addition, interviews with teachers were also conducted and got the results that the teacher felt that this learning device made it easier to learn in class, the learning steps in the lesson plan were clear, it's just that the method had to be rethought so that all students could be active in the discussion because there were still some students who were passive during the discussion, but thankfully all students were enthusiastic because the appearance of the application was attractive so that it fostered their desire to learn. The teacher also suggests paying attention to the problem of instructions that must be conveyed to students in operating the application so that there are no questions or confusion for students during operation, because if this happens, of course, it will hamper learning in class and not under the time allocation that has been designed as intended. Occurred during a limited trial.

The way students answer and students' answer to essay questions has also improved because usually, students will immediately be confused about which formula to use to answer story questions, and the sequence of the problem-solving process is sometimes also incomplete, but after using the application, almost all students are correct in the sequence, it's just that there are still students who are wrong in the calculations and changes in the units that are asked for questions when seen in students' answers to the problem-solving test given at the end of the study. Overall, the results of interviews with several students and teachers responded very positively to the use of these learning device and stated that these learning device were able to increase students' learning motivation and mathematical problem-solving abilities.

The characteristics of the learning device are:

1)     Lesson plans, in accordance with the learning process, is in the form of activities adapted to other devices developed. Lesson plans makes it easy and helps teachers learn in school classes. One of them makes it easier to direct students to know, this is because the lesson plans contains the learning steps that the teacher must do clearly and has been adapted to the contextual approach used. In connection with the obstacles faced from the limited trial to the first field trial, each lesson gradually decreased.

2)     The student book that was successfully developed in this study is a student book that is used as a student companion in learning mathematics in class IX, which is focused on the subject of curved side space. Examples of questions in student books are related to everyday life and will guide students to answer problem-solving questions in accordance with mathematical problem-solving indicators.

3)     Student worksheets emphasizes learning on the discovery of the concept of curved side space by activities carried out by students. The student worksheets developed requires students to actively use their five senses and knowledge as students construct their knowledge with the guidelines or steps that exist in each student worksheets activity. For example, in finding objects, the characteristics, and formulas for the surface area and volume of curved side spaces. Students are asked to solve problems that commonly occur in everyday life by using the stages of solving mathematical problems so that students will get used to solving problems according to the indicators of solving mathematical problems. On the worksheet, there is an icon linked to the GeoGebra applet on geogebra.org, so students don't need to install the GeoGebra application on their gadgets. The GeoGebra applet will help students construct their knowledge.

4)     Learning device that include student worksheets and student books are presented in one application called "Math in Dimension" this application was made using the Articulate Storyline 3 application, in terms of the features of this application, it is exciting, it looks not just reading, but students are required to be active in its operation. For example, to match questions and answers on the student worksheets using drag and drop, students can type their answers directly into the application, at the end, the scores they get will immediately come out. Besides that, students can see their solutions on which questions are wrong. To enter each student worksheets material, a password is required that is given at the beginning of the meeting so that students cheating in doing the student worksheets before the time can be prevented. Students' books can only be read after completing the student worksheets, so students will be required to construct their knowledge when working on the student worksheets. The Math in Dimension application is practical because it can be used anywhere and anytime, using online and offline learning modes. The data size is not large, so it doesn't take up a lot of student memory when installed.

5)     Math problem-solving test is a test used to measure the effectiveness of learning device. This test has four questions whose sentences are easy for students to understand and uses story questions that are close to students so that students are interested and feel challenged to find solutions to these problems. The allocation of time given to work on these questions also follows students' average ability.

While the characteristics of the implementation of online learning device are :

1)     Learning device are flexible because they can be applied to both online and offline learning modes, as was the case when conducting research. In the middle of the study, there was a change in the method of learning in schools from online mode to offline mode. Although there are changes in learning modes, learning device can also be used in offline learning modes. So that use is not limited to online learning modes only.

2)     In the implementation of learning, students can recognize and explore GeoGebra applets connected to the Math in Dimension application in the student worksheets section of tube and ball material. By using geogebra.org, students can use it without having to install the GeoGebra application on their gadgets. Students can try it themselves by sliding the slider on how the tube is opened so that they can see the nets of the tube and can change the size of the radius of the circle from the tube. For the GeoGebra applet, students can see how to find the formula for the surface area of a sphere and try to change the radius of the sphere and how the change in the radius of the sphere affects the surface area of the sphere. And how is the relation between the surface area of a sphere and the area of a circle with the same radius . So it can be said that students can construct their knowledge by using the GeoGebra applet on the worksheet.

3)     The Math in Dimension application is elementary to use. It can increase students' learning motivation and mathematical problem-solving abilities because the questions in the application will guide students to answer according to mathematical problem-solving indicators.

 

4. CONCLUSIONS

This research has succeeded in developing online learning device with a valid, practical, and effective contextual approach to improving students' mathematical problem-solving abilities. It has characteristics that distinguish them from other learning device.

·        characteristics of the learning device in this study are (1) the lesson plans developed to make it easier for teachers in the learning process because the steps are clear and follow the contextual approach (2) The student books and student worksheets contain problems that are close to students' lives according to the contextual approach (3) Student books and worksheets are made in the form of practical applications because they can be used anywhere and anytime (4) Math in Dimension applications have exciting features (5) Problem-solving tests with questions that are easy for students to understand and make students interested in solving them because problems that are taken are commonplace in life.

·        characteristics of the implementation of the learning devices in this study are (1) the learning devices developed can be adapted for application in online and offline modes (2) In practice, students can explore tube and ball material using the Geogebra applet, which is connected to the Math in Dimension application without the need to install GeoGebra application (3) Math in Dimension application is easy to use and can increase students' learning motivation and mathematical problem-solving ability.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Aminah, N., and Irawati, I. (2018). Pengembangan Perangkat Pembelajaran Dengan Pendekatan Kontekstual Pada Materi Kubus Dan Balok. TEOREMA: Teori Dan Riset Matematika, 3(2), 137. https://doi.org/10.25157/teorema.v3i2.1178. 

Arifin, Yusmin, E., and Hamdani. (2017). Analisis Kesulitan Belajar Siswa pada Materi Bangun Ruang Sisi Lengkung di SMP. Jurnal Pendidikan Dan Pembelajaran (JPP), 6(4), 1-13. http://dx.doi.org/10.26418/jppk.v6i4.19848. 

Barata, A. (2015). Pengembangan Perangkat Pembelajaran Matematika Pada Materi Perbandingan Dengan Pendekatan Konstestual. In Yogyakarta : Universitas Negeri Yogyakarta, 235.

Entyka M. R., and Riyadi, M. (2016). Analisis Kesalahan Siswa Dalam Pemecahan Masalah Berdasarkan Pendapat John W. Santrock Pada Pokok Bahasan Bangun Ruang Sisi Lengkung Ditinjau Dari Gaya Belajar Dan Gaya Berpikir Siswa. Jurnal Elektronik Pembelajaran Matematika, 4(10), 973-981.

Keengwe, J., and Georgina, D. (2012). The Digital Course Training Workshop for Online Learning and Teaching. Education and Information Technologies. https://doi.org/10.1007/s10639-011-9164-x.

Makmuri, M., Wijayanti, D. A., Salsabila, E., and Nur Fadillah, R. (2021). Pengembangan Aplikasi Pembelajaran Matematika Berbasis Android Dengan Pendekatan Kontekstual Pada Materi Persamaan Garis Lurus Untuk Peserta Didik Kelas VIII. Jurnal Cendekia: Jurnal Pendidikan Matematika, 5(1), 643-654. https://doi.org/10.31004/cendekia.v5i1.535. 

Muslich, M. (2007). KTSP Pembelajaran Berbasis Kompetensi Dan Kontekstual: Panduan Bagi Guru, Kepala Sekolah, Dan Pengawas Sekolah. Bumi Aksara.

Nuraida, I. (2017). Analisis Kesalahan Penyelesaian Soal Bangun Ruang Sisi Lengkung Siswa Kelas Ix Smp Negeri 5 Kota Tasikmalaya. Teorema, 1(2), 25.  https://doi.org/10.25157/.v1i2.550.

Parwati, N. N., Sudiarta, I. G. P., Mariawan, I. M., and Widiana, I. W. (2018). Local Wisdom-Oriented Problem-Solving Learning Model to Improve Mathematical Problem-Solving Ability. Journal of Technology and Science Education, 8(4), 310-320. https://doi.org/10.3926/jotse.401. 

Plomp, T. (2007). Educational Design Research : An Introduction. Netherlands Institute for Curriculum Development.

Sugiantara, I. G. P. A., Sadra, I. W., and Suparta, I. N. (2013). Matematika Realistik Dengan Peta Konsep Pada Materi Trigonometri di Kelas XI SMK. E-Journal Program Pascasarjana Universitas Pendidikan Ganesha, 2(2).

Suherman. (2015). Kreativitas Siswa Dalam Memecahkan Masalah Matematika Materi Pola Bilangan Dengan Pendekatan Matematika Realistik (PMR). Al-Jabar.  https://doi.org/10.24042/ajpm.v6i1.57.

Surya, E., Putri, F. A., and Mukhtar. (2017). Improving Mathematical Problem-Solving Ability and Self-Confidence of High School Students Through Contextual Learning Model. Journal on Mathematics Education, 8(1), 85-94. https://doi.org/10.22342/jme.8.1.3324.85-94.