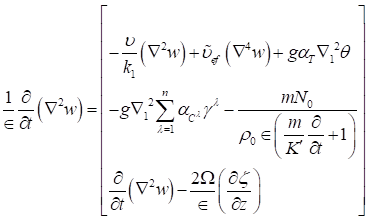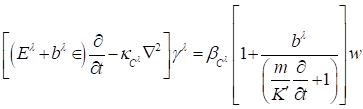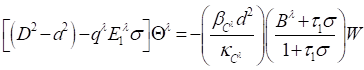Kumar et al. (2017).

Convective instability in a rotating frame has numerous applications in rotating machinery, food processing industry, centrifugal casting of metals and in thermal power plants (to generate electricity by rotation of turbine blades). Rudraiah (1986) considered the effect of rotation on linear and non-linear double-diffusive convective problem saturating a porous layer.

In geophysical context, the fluid is often not pure but may instead be permeated with dust particles. These suspended particles have scientific relevance in geophysics, chemical engineering, and astrophysics Mcdonnel (1978). Scanlon and Segel (1973) considered the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number was reduced solely because the heat capacity of the pure fluid was supplemented by that of the particles.

The intention of the present paper is to analyse theoretically the onset of thermal convection in a multi-diffusive fluid layer in the presence of suspended dust particles, uniform vertical rotation saturating a porous medium. Most research outcomes for porous medium flows are based on the Darcy model which gives appropriate results at small Reynolds number. Therefore, Darcy-Brinkman model is employed for porous medium which is considered physically more realistic than the usual Darcy model and also gave satisfactorily result at large Reynolds number and for high porosity porous medium by incorporating the inertial and viscous effects in addition to the usual Darcy model. The research on multi-component fluid layer through porous medium has notable geophysical relevance in real life and is increasing with the number of salts dissolved in it.

 

2.    PROBLEM FORMULATION AND LINEAR STABILITY ANALYSIS

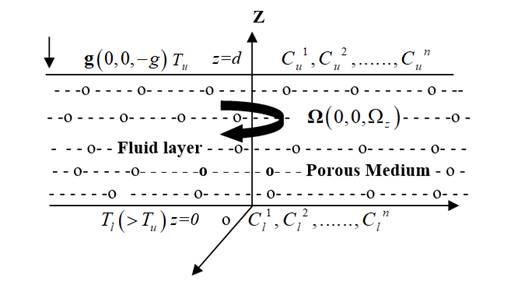
Consider an infinite horizontal Boussinesq fluid layer permeated with dust particles lying in the region  through a Darcy-Brinkman porous medium under the effect of a uniform vertical rotation. Both the boundaries are maintained at uniform temperatures and and uniform concentrations  andwith gravity acting in vertical downward direction (Figure 1).

Figure 1 Geometrical sketch of the physical problem

 

The governing equations of motion and continuity for an incompressible Boussinesq (1903) fluid layer saturating a Darcy-Brinkman porous medium Brinkman (1947a) are as:

 

                                    

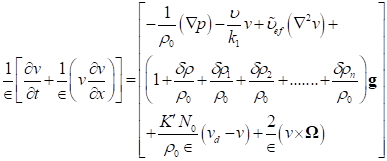
                                                                                                                                                                   Equation 1

 

                                                                                                                Equation 2

 

where,denote, respectively, the time, the reference density, fluid density, effective porosity, pressure, kinematic viscosity, effective kinematic viscosity, fluid velocity components, particles velocity, effective permeability, number density of suspended particles and the gravitational acceleration vector. The termis the Stoke’s drag co-efficient.

The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. Inter-particle reactions are ignored as the distances between the particles are assumed to be quite large compared with their diameters.

The governing equations of motion and continuity for the particles (ignoring the pressure, magnetic field, and gravity) are as:

 

                                                                  Equation 3

 

                                                                                                                                                                                    Equation 4

 

where is the mass of particles per unit volume.

The equations for temperature field and solute concentrations are as:

 

 

 

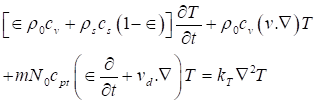                                           Equation 5

 

where,  denote, respectively, the density of solid material, heat capacity of solid material, the specific heat at constant volume, heat capacity of suspended particles, the temperature, and the coefficient of heat conduction.

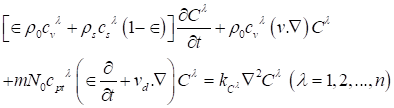                                                                                                                           Equation 6

 

The symbolsdenote the analogoussolute components.

The density is taken as a linear function of temperature field and salt concentrations as:

 

                                   Equation 7

 

where,  denote, respectively, the temperature at lower boundary, temperature at upper boundary, coefficient of thermal expansion, coefficients of solute expansion, concentration components at lower and upper boundaries.

The basic state is assumed to be stationary and therefore, for determining the stability/instability of the system linear stability analysis procedure followed by normal mode method is adopted by introducing small infinitesimal perturbations in the basic variables.

The basic state of the system is defined as:

 

                                                                                                                                                      Equation 8

 

Let the perturbations in the basic variables given in Equation 8 are defined as:

 

 

 

 

                                                                                                                         Equation 9

So, the resulting linearized perturbation equations after eliminating the pressure gradient term are as:

                                    Equation 10

         

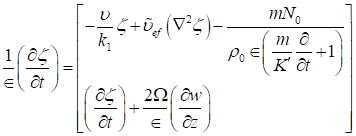                                            Equation 11

 

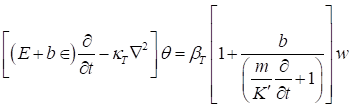                                                                                                                                                                              Equation 12

 

                                    Equation 13

 

The change in density  due to temperature variation and concentration variationsis given by

 

                                                                                                                                                                                                   Equation 14

 

where, in Equation 10, Equation 13 denote, respectively, the thermal diffusivity, the solute diffusivity, vertical component of fluid velocity, vertical component of suspended particles velocity, vertical component of vorticity, horizontal Laplacian operator and Laplacian operator, with

 

 

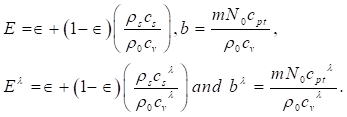
3.    NORMAL MODE METHOD AND DISPERSION RELATION

A normal mode representation is assumed in various physical disturbances with a dependence on of the form:

 

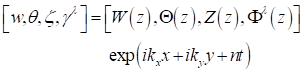                                                                                                                                                                                              Equation 15

 

where,are the wave numbers alongdirections, respectively.

Using expression Equation 15, the non-dimensional form of Equation 10, Equation 13 (after dropping the asterisk for convenience) are as:

 

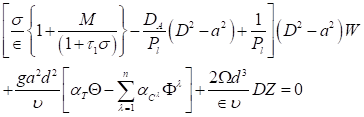                                                                                                                                                        Equation 16

 

                                                                                                                                                                          Equation 17

                                                      

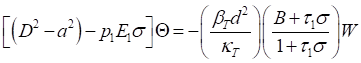                                     Equation 18

 

                                     Equation 19

The above perturbation equations (16)-(19) are non-dimensionalized using the following scaling’s:

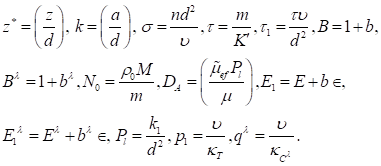
where, is the dimensionless medium permeability, is the thermal Prandtl number, are the Schmidt numbers, is the adverse temperature gradient, are the solute concentration gradients,  is a wave number and  is the frequency of the harmonic disturbance and

The boundary conditions (for the case of two free boundaries are defined as:

 

                                                                                                                                                                          Equation 20

 

Eliminatingfrom equations Equation 16, Equation 19 a dispersion relation in  is obtained as:

 

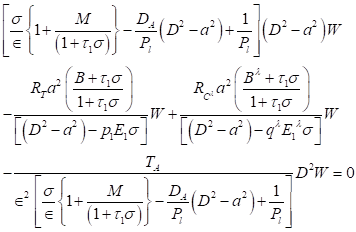                                                                                                                                                      Equation 21

 

where, (thermal Rayleigh number),   (solute Rayleigh numbers),   (Taylor number).

 

4.    THE STATIONARY CONVECTION

For stationary state, Equation 21 yields an expression of the form:             

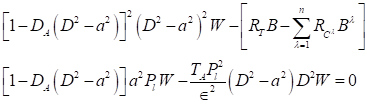                                                                                                                                                   Equation 22

                                                             

Since all the even derivatives ofvanishes, so considering an appropriate solution for of the form:

Equation                                                      Equation 22 yields:

 

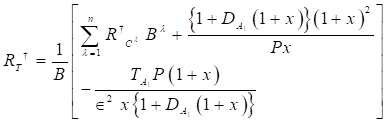                                                                                                                                                 Equation 23

 

where, the following notations are assumed as:

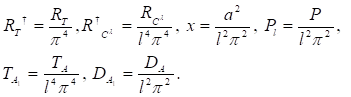Minimizing Equation 23 with respect to yields a fifth-degree equation in  as:

 

                                                                                                                                                                Equation 24                                                                                                                                                                           

where,           

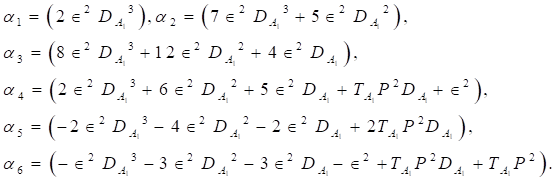
The critical dimensionless wave numberfor varying values of parameters can be obtained from Equation 24 and then the critical thermal and solute Rayleigh numbers can be deduced from Equation 23.

Equation 23 represents a relationship between thermal and solute Rayleigh numbers in terms of various embedded parameters. The effect of these parameters (suspended particles, medium permeability, medium porosity, Taylor number, Darcy-Brinkman) on thermal Rayleigh number can be examined analytically from the following derivatives

 

5.    CONCLUSION

A linear stability analysis followed by normal mode method is taken into account to discuss the effect of uniform vertical rotation and suspended particles on the onset of multi-diffusive convection through a Darcy-Brinkman porous medium and a dispersion relation is obtained in terms of thermal and solute Rayleigh numbers. Further, the case of stationary convection is also discussed and a relationship between thermal and solute Rayleigh numbers is obtained to study the effect of various embedded parameters. The critical thermal and solute Rayleigh numbers can be obtained with the help of critical dimensionless wave number for varying values of physical parameters.

 

ACKNOWLEDGMENTS

One of the authors, Dr B.K. Singh, thanks the School of Science & Department of Mathematics, IFTM University, Moradabad-244001 (India), for financial support. Further, Dr B.K. Singh is for providing useful suggestions.

 

REFERENCES

Boussinesq, J. (1903). Theorie analytique de la Chaleur. Gauthier-Villars 2, 172. https://books.google.co.uk/books/about/Theorie_analytique_de_la_Chaleur.html?id=O08NmgEACAAJ&redir_esc=y

Brinkman, H.C. (1947a). A Calculation of The Viscous Force Exerted By A Flowing Fluid on A Dense Swarm of Particles. Applied Scientific Research, A1, 27-34. Https://Doi.Org/10.1007/BF02120313  

Brinkman, H.C. (1947b). On The Permeability of Media Consisting of Closely Packed Porous Particles. Applied Scientific Research, A1, 81-86. Https://Doi.Org/10.1007/BF02120318

Chandrasekhar, S.C. (1981). Hydrodynamic and Hydromagnetic Stability. New York : Dover Publication. https://books.google.co.uk/books/about/Hydrodynamic_and_Hydromagnetic_Stability.html?id=oU_-6ikmidoC&redir_esc=y

Huppert, H., & Turner, J. (1981). Double-Diffusive Convection. Journal of Fluid Mechanics, 106, 299-329. Https://Doi.Org/10.1017/S0022112081001614  

Kumar, K., Singh, V., Sharma, S. (2017). Effect of Horizontal Magnetic Field and Horizontal Rotation on Thermosolutal Stability of a Dusty Couple-Stress Fluid through a Porous Medium : à Brinkman Model. Journal of Applied Fluid Mechanics, 10(2), 681-692. Https://Doi.Org/10.18869/acadpub.jafm.73.239.27027  

Mcdonnel J.A.M. (1978). Cosmic Dust. Toronto : John Wiley & Sons. https://www.abebooks.co.uk/9780471995128/Cosmic-Dust-MCDONNELL-JAM-0471995126/plp

Nield, D.A. And Bejan, A. (2006). Convection In Porous Media. New-York : Springer Science & Business Media. https://books.google.co.uk/books/about/Convection_in_Porous_Media.html?id=tG8sxSHrPEIC&redir_esc=y

Prakash, J., Singh, V., Kumar, R. And Kumari, K. (2016). The Onset of Convection In A Rotating Multicomponent Fluid Layer. Journal of Theoretical and Applied Mechanics, 54 (2), 477-488. Https://Doi.Org/10.15632/Jtam-Pl.54.2.477

Radko, T. (2013). Double-Diffusive Convection. Cambridge University Press. Https://Doi.Org/10.1017/CBO9781139034173

Rionero, S. (2013a). Multi-Component Diffusive-Convective Fluid Motions In Porous Layer Ultimately Boundedness, Absence of Subcritical Instabilities And Global Nonlinear Stability For Any Number of Salts. Physics of Fluids, 25, 1-23. Https://Doi.Org/10.1063/1.4802629

Rionero, S. (2013b). Triple Diffusive Convection In Porous Media, Acta Mechanics, 224, 447-458. Https://Doi.Org/10.1007/S00707-012-0749-2

Rudraiah, N., Shivakumara, I.S. And Friedrich, R. (1986). The Effect of Rotation on Linear And Non-Linear Double-Diffusive Convection In A Sparsely Packed Porous Medium. International Journal of Heat and Mass Transfer, 29(9), 1301-1317. Https://Doi.Org/10.1016/0017-9310(86)90163-8

Scanlon, J.W. And Segel, L.A. (1973). Some Effects of Suspended Particles on The Onset of Bénard Convection. The Physics of Fluids, 16, 1573-1578. Https://Doi.Org/10.1063/1.1694182

Straughan, B. And Tracey, J. (1999). Multi-Component Convection-Diffusion With Internal Heating And Cooling. Acta Mechanica, 133, 219-239. Https://Doi.Org/10.1007/BF01179019

Terrones, G. And Pearlstein, A.J. (1989). The Onset Of Convection In A Multicomponent Fluid Layer. The Physics of Fluids, 5(9), 2172-2182. Https://Doi.Org/10.1063/1.857381

Tracey, J. (1996). Multi-Component Convection-Diffusion In A Porous Medium, Continuum Mechanics and Thermodynamics, 8(6), 361-381. Https://Doi.Org/10.1007/S001610050050

Turner, J.S. (1985). Multicomponent Convection. Annual Review of Fluid Mechanics, 17, 11-44. Https://Doi.Org/10.1146/Annurev.Fl.17.010185.000303