solution of Navier-Stokes equations for laminar boundary layer slip flow over a stretching surface. Ganesan and Loganathan [Ganesan and Loganathan (2003)] investigated magnetic field effect on moving vertical cylinder with constant heat flux. Cortell [Cortell (2005)] considered suction/blowing and internal heat generation/absorption in flow and heat transfer of a fluid through porous medium over a stretching surface. Flow and heat transfer in an asymmetric stagnation flow on a cylinder was studied by Elbarbary and Elgazery [Elbarbary and Elgazery (2005)]. Xu, Liao [Xu and Liao (2005)] and Hayat et al. [Hayat  et al. (2006)] used homotopy analysis method to study MHD Flow of non-Newtonian and Maxwell fluids over stretching plate.

The flow past a stretching cylinder has many industrial and engineering applications for example in metallurgy and polymer industries such as extraction and manufacture of polymer and rubber sheets glass fiber production etc. Ishak et al. [Ishak et al. (2008), Ishak  and Nazar (2009) and Ishak et al. (2008)] examined the boundary layer flow and heat transfer due to stretching cylinder with uniform suction/blowing effect and external magnetic field. Later Mukhopadhyay [Mukhopadhyay (2013), Mukhopadhyay (2011)] extended the work of Ishak by including chemically reactive solute transfer and slip flow along a stretching cylinder. Hayat et al. [Hayat  et al. (2018)] discussed convective heat and mass transfer by an inclined stretching cylinder. Stagnation-point flow and heat transfer over an exponentially stretching/shrinking cylinder was studied by Merkin et al. [Merkin et al. (2017)]. Yu et al. [Yu et al. (2018)] investigated effects of thermal buoyancy on flow and heat transfer around a permeable circular cylinder with internal heat generation. In our previous paper [Sinha and Yadav  (2021)], the influence of heat source/sink on MHD mixed convective flow along a vertical stretching cylinder saturated in porous medium was investigated.

Aim of the present paper is to investigate the effects of thermal radiation and velocity slip on steady MHD slip flow of viscous incompressible electrically conducting fluid over a permeable stretching cylinder saturated in porous medium in the presence of external magnetic field.

 

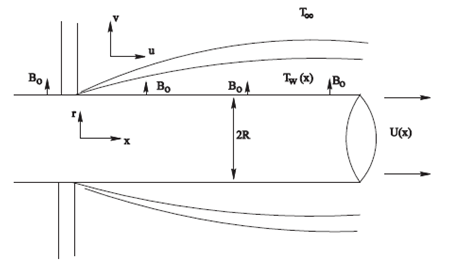
2.    MATHEMATICAL FORMULATION OF THE PROBLEM

Consider steady axisymmetric flow of viscous incompressible electrically conductive fluid over a permeable stretching horizontally placed cylinder of radius R in the presence of external magnetic field . The uniform magnetic field  is applied normal to the surface of the cylinder which is saturated in porous medium. The  and  axis are taken as the axis of the cylinder and in the radial directions respectively. To neglect the induced magnetic field, it is assumed that the magnetic Reynolds number is very small. The governing equations of continuity, motion and energy are as follows:

Figure 1 Physical model of the problem

 

                                                                                              (1)

 

                                                               (2)

 

                         (3)

 

Where  and  are the velocity components in  and  directions,  is the kinematic viscosity,  is density of the fluid,  is the coefficient of viscosity,  is the electrical conductivity, is permeability of the porous medium,  is temperature of the fluid,  is thermal diffusivity and  is external volumetric heat source/sink.For the radiated heat flux Rosseland approximation is used and is approximated by truncated Taylor series about .

Corresponding boundary conditions are given by

 

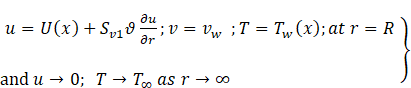                                       (4)

 

Where  is the stretching velocity,    is the prescribed wall temperature,   and  are the reference velocity and temperature respectively,   is ambient temperature,  is characteristic length,  is velocity slip and is temperature exponent.

 

 

 

 

3.    METHOD OF SOLUTION

In order to get solution of equation (1) to (3) with boundary conditions (4), introducing the following similarity variable, stream function and dimensionless functions

 

 , ,                                                        (5)

 

Where  and so that the equation of continuity is automatically satisfied. Equations (2) to (4) reduce to

 

                                                 (6)

 

      (7)

 

                                                                   (8)

Where prime denotes differentiation with respect to ,  is the curvature parameter,  is the permeability parameter, is the magnetic parameter,is the heat source/sink parameter,  is the Prandtl number,  is the radiation parameter, is the slip parameter and  is suction/injection parameter.

The physical quantities of interest are the skin friction coefficient  and local Nusselt number  defined as

 

,                                                                                  (9)                                                                         

 

The wall shear stress  and the heat flux at the wall  are given by

 , 

Where  and  are the coefficient of viscosity and thermal conductivity of the fluid respectively.

Using similarity transformation (5) in (9), the skin friction coefficient and local Nusselt number reduce to

 , .

Since equations (6) and (7) are highly nonlinear, these equations with boundary conditions (8) are converted into system of first order differential equations as given below

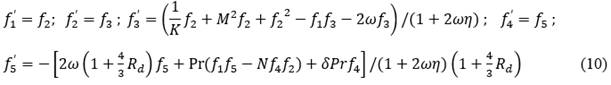
with boundary conditions

 

                                                      (11)

 

Where  and  System of first order differential equations given in (10) is solved numerically by Runga-Kutta (fourth order) method, but in (11) only three initial conditions are given. To overcome this problem shooting technique is used, the initial guesses for  and  are assumed to be  and  . To validate the assumed values of  and , calculated values of and  at the upper boundary () are compared with the values given in (11). The procedure is repeated until the results upto the desired degree of accuracy () are obtained.

 

4.     RESULTS AND DISCUSSIONS

Effects of various physical parameters e.g., curvature parameter, magnetic parameter, velocity slip parameter, temperature exponent, radiation parameter, Prandtl number, permeability parameter, heat source/sink parameter and suction/injection parameter on fluid velocity and temperature are shown through figures 2 to 9. Skin friction coefficient and Nusselt number for different values of these parameters are tabulated and discussed through Table 1.

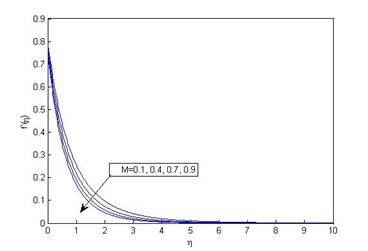
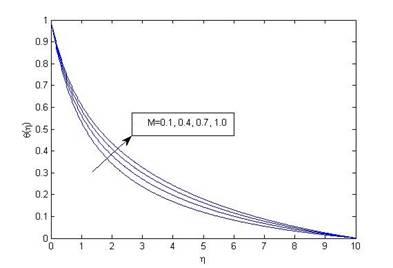
Effect of magnetic parameter on fluid velocity and temperature are shown through Figure 2(a) and Figure 2 (b).

Figure 2 (a) Variation of velocity f'(η) with η for various values of magnetic parameter (M) when ω=0.25, Pr=1, R_d=0.1, N=1, δ=0.1, S=0.1, S_v=0.2 and K=10.

 

Figure 2 (b) Variation of temperature θ(η) with η for various values of magnetic field parameter (M) when  ω=0.25, Pr=1, R_d=0.1, N=1, δ=0.1, S=0.1, S_v=0.2 and K=10.

 

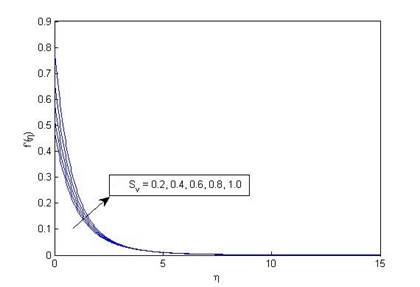
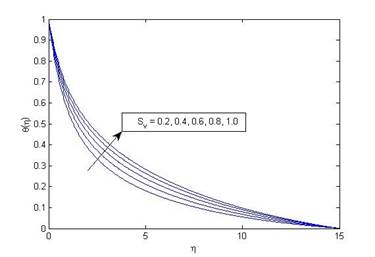
When magnetic field increases, a resistive force (Lorentz force) works against the flow of the fluid which results in decreasing fluid velocity and increasing fluid temperature. It is consistent with the data given in Table 1 which shows that skin friction decreases with decreasing fluid velocity while Nusselt number increases with increasing temperature difference. Figure 3(a) and Figure 3 (b) represent that both fluid velocity and temperature increase with enhancing values of velocity slip parameter. This is because there is a jump in velocity of the fluid layers adjacent to the wall due to increasing velocity slip parameter.

Figure 3 (a) Variation of velocity f'(η) with η for various values of slip parameter (S_v) when ω=0.25, M=0.1, Pr=1,  R_d=0.1, N=1, δ=0.1, S=0.1 and K=10

 

Figure 3 (b) Variation of temperature θ(η) with η for various values of slip parameter (S_v) at ω=0.25, M=0.1, Pr=1, R_d=0.1, N=1, δ=0.1, S=0.1 and K=10.

 

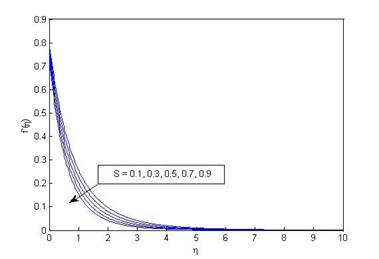
Figure 4 (a) Variation of velocity f'(η) with η for various values of suction/injection parameter (S) when ω=0.25, M=0.1, Pr=1, R_d=0.1, N=1, δ=0.1, S_v=0.2 and K=10.

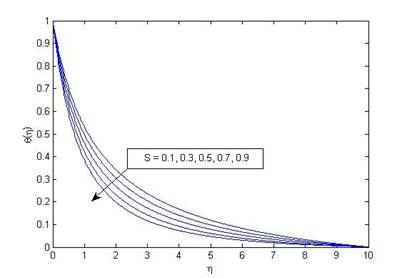
Figure 4(b) Variation of temperature θ(η) with η for various values of suction/injection parameter (S) when ω=0.25, M=0.1, Pr=1, R_d=0.1, N=1, δ=0.1, S_v=0.2 and K=10.

 

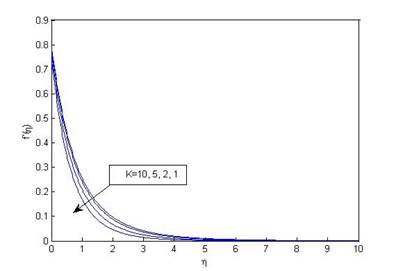
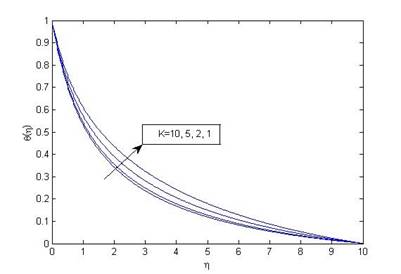
Fluid velocity and temperature decrease with increasing suction parameter as depicted in Figure 4 (a) and Figure 4 (b). The physics behind this is when suction parameter increases some amount of fluid is sucked by the wall. Also, due to decreasing fluid velocity and temperature skin friction decreases while Nusselt number increases which can be verified from Table 1. Effect of permeability parameter on fluid velocity and temperature are shown through Figure 5 (a) and Figure 5 (b). When permeability parameter increases fluid velocity increases while temperature decreases. This is because increasing permeability parameter shows more assistance to the fluid flow and as a result fluid temperature decrease.

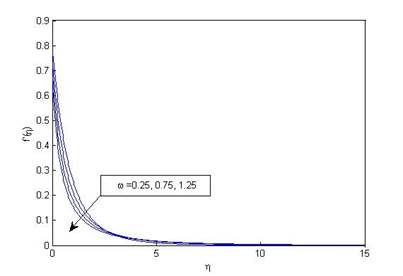
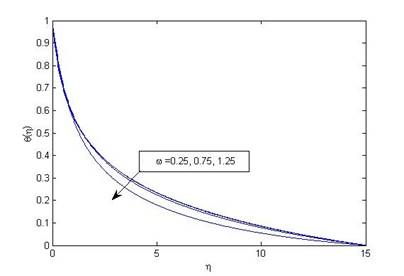
Figure 6(a) and Figure 6 (b) represent that both fluid velocity and temperature decrease with increasing curvature parameter.

Figure 5 (a) Variation of velocity f'(η) with η for various values of permeability parameter (K) when ω=0.25, M=0.1, Pr=1,R_d=0.1, N=1, δ=0.1, S=0.1 and S_v=0.2.

 

Figure 5 (b) Variation of temperature θ(η) with η for various values of permeability parameter (K) when ω=0.25, M=0.1, Pr=1, R_d=0.1, N=1, δ=0.1, S=0.1 and S_v=0.2.

 

Figure 6 (a) Variation of velocityf'(η) with η for various values of curvature parameter (ω)when M=0.1, Pr=1, R_d=0.1, N=1, δ=0.1, S=0.1, S_v=0.2 and K=10.

 

Figure 6 (b) Variation of temperature θ(η) with η for various values of curvature parameter (ω) when M=0.1, Pr=1, R_d=0.1, N=1, δ=0.1, S=0.1, S_v=0.2 and K=10.

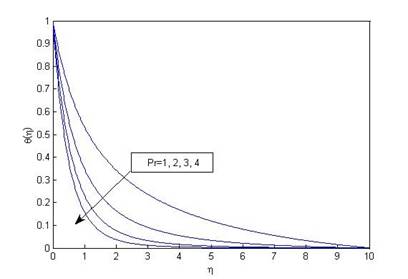
Figure 7 Variation of temperature θ(η) with η for various values of Prandtl number (Pr) when ω=0.25, M=0.1, R_d=0.1, N=1, δ=0.1, S=0.1, S_v=0.2 and K=10.

 

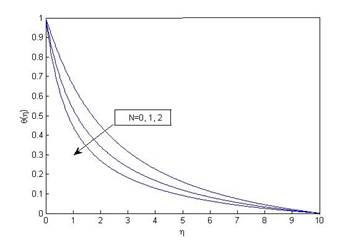
Figure 8 Variation of temperature θ(η) with η for various values of temperature exponent (N) when ω=0.25, M=0.1, Pr=1, R_d=0.1, δ=0.1, S=0.1, S_v=0.2 and K=10.

 

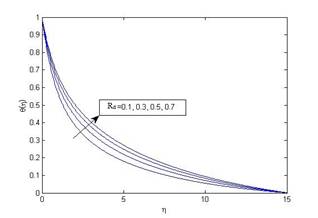
Figure 7 and Figure 8 depict that fluid temperature decreases with increasing Prandtl number or temperature exponent, while Figure 9 shows that temperature increases with increasing radiation parameter. When radiation parameter increases fluid elements consumes the radiated heat and get energized and as a result fluid temperature increases and Nusselt number decreases.

Figure 9 Variation of temperature θ(η) with η for various values of radiation parameter (R_d) when ω=0.25, M=0.1, Pr=1, N=1, δ=0.1, S=0.1, S_v=0.2 and K=10.

 

Variation in skin friction coefficient () and Nusselt number () with respect to physical parameters are given in Table 1. The table shows that skin friction coefficient decreases when magnetic parameter, suction parameter or curvature parameters increases while it increases when velocity slip parameter or permeability parameter increases. Moreover, the table illustrate that the Nusselt number of the flow field decreases as the values of magnetic parameter, radiation parameter or velocity slip parameter increases, and it increases as the values of curvature parameter, Prandtl number, temperature exponent, suction parameter or permeability parameter increases.

Table 1 Numerical values of Skin friction coefficient  and Nusselt number  for various values of physical parameters when .
	M	Pr	Rd	N	S		K
0.25	0.1	1	0.1	1	0.1	0.2	10	-0.99027	0.75980
1.25								-1.41780	0.97500
	0.4							-1.075795	0.74510
	1.0							-1.213036	0.66515
		1							0.79765
		4							1.99500
			0.3						0.65800
			0.7						0.53800
				1				-0.990850	0.79765
				2				-0.990850	1.09190
					0.3			-1.06145	0.88200
					0.7			-1.21006	1.08500
						0.4		-0.798670	0.68200
						1.0		-0.515815	0.53650
							1	-1.213036	0.66550
							10	-0.990850	0.79765

 

Table 2 Comparison of numerical values of Nusselt number for different temperature exponents with previously published results when ω=0.0, M= 0.0 and Pr=1.
N	Ishak and Nazar [18]	Grubka and Bobba [Grubka and Bobba (1985) +	S. Mukhopadhyay [21]	Present study
0	0.5820	0.5820	0.5821	0.5720
1	1.0000	1.0000	1.0000	0.9870
2	1.3333	1.3333	1.3332	1.3201

 

Table 2 shows the comparison of Nusselt number for different values of temperature exponent with previous studies. The numerical results reveal that our results are in an excellent agreement with the results given by Ishak and Nazar [Ishak  et al. (2008)], Grubka and Bobba [Grubka and Bobba (1985)], S. Mukhopadhyay [Mukhopadhyay (2013)] in limiting conditions.

 

5.    CONCLUSIONS AND RECOMMENDATIONS

The numerical study has been done to examine the influence of thermal radiation and slip on velocity and heat transfer of MHD boundary layer flow over a stretching cylinder. From the study the following conclusions are drawn:

Fluid velocity and skin friction coefficient increase with increasing velocity slip parameter or permeability parameter.

Fluid velocity and skin friction coefficient decrease with increasing curvature parameter, magnetic parameter or suction/injection parameter.

Fluid temperature increases while Nusselt number decreases with increasing magnetic parameter, velocity slip parameter or radiation parameter.

Fluid temperature decreases while Nusselt number increases with increasing curvature parameter, suction parameter, permeability parameter, temperature exponent or Prandtl number.

 

ACKNOWLEDGEMENTS

The authors would like to thank the Editor and anonymous reviewers for their careful reading and constructive comments and suggestions, which helped a lot in the improvement of the manuscript.

 

REFERENCES

Ali, M.E. (1994). Heat transfer characteristics of a continuous stretching surface. Heat Mass Transfer, 29(4), 227-234. Retrieved from https://doi.org/10.1007/BF01539754

Anderson, H.I. (2002). Slip flow past a stretching surface. Acta Mechanica, 158, 121-125. Retrieved from https://doi.org/10.1007/BF01463174

Ariel, P.D., Hayat, T. and Asghar, S. (2006). The flow of an elastico-viscous fluidpast a stretching sheet with partial slip. Acta Mechanica, 187, 29-35. Retrieved from https://doi.org/10.1007/s00707-006-0370-3

Chen, C.K. and Char, M.I. (1988). Heat transfer of a continuous stretching surface with suction or blowing. Journal of Mathematical Analysis and Applications, 135(2), 568-580. Retrieved from https://doi.org/10.1016/0022-247X(88)90172-2

Cortell, R. (2005). Flow and heat transfer of a fluid through a porousmedium over a stretching surface with internal heat generation/absorption and suction/blowing. Fluid Dynamics Research, 37(4), 231-45. Retrieved from https://doi.org/10.1016/j.fluiddyn.2005.05.001

Crane, L.J. (1970). Flow past a stretching plate. Zeitschrift Für Angewandte Mathematik Und Physik (ZAMP), 21(4), 645-647. Retrieved from https://doi.org/10.1007/BF01587695

Elbarbary, E.M.E. and Elgazery, N.S. (2005). Flow and heat transfer of a micropolar fluid in an axisymmetric stagnation flow on a cylinderwith variable properties and suction (numerical study). Acta Mechanica, 176, 213-229. Retrieved from https://doi.org/10.1007/s00707-004-0205-z

Fang, T., Zhang, J. and Yao, S. (2009). Slip MHD viscous flow over a stretching sheet - An exact solution. Communications in Nonlinear Science and Numerical Simulation, 14, 3731-3737. Retrieved from https://doi.org/10.1016/j.cnsns.2009.02.012

Ganesan, P. and Loganathan, P. (2003). Magnetic field effect on a moving vertical cylinder with constant heat flux. Heat Mass Transfer, 39, 381-386. Retrieved from https://doi.org/10.1007/s00231-002-0383-y

Grubka, L.G. and Bobba, K.M. (1985). Heat transfer characteristics of a continuous stretching surface with variable temperature. The ASME Journal of Heat Transfer, 107, 248-250. Retrieved from https://doi.org/10.1115/1.3247387

Gupta, P.S. and Gupta, A.S. (1977). Heat and mass transfer on a stretching sheet with suction and blowing. The Canadian Journal of Chemical Engineering, 55, 744-756. Retrieved from https://doi.org/10.1002/cjce.5450550619

Hayat, T., Abbas, Z. and Sajid, M. (2006). Series solution for the upper-convected Maxwell fluid over a porous stretching plate. Physics Letters A, 358, 396-403. Retrieved from https://doi.org/10.1016/j.physleta.2006.04.117

Hayat, T., Saeed, Y., Asad, S. and Alsaedi, A. (2018). Convective heat and mass transfer in flow by an inclined stretching cylinder. Journal of Molecular Liquids, 220, 573-580. Retrieved from https://doi.org/10.1016/j.molliq.2016.03.047

Ishak, A. and Nazar, R. (2009). Laminar boundary layer flow along a stretching cylinder. European Journal of Scientific Research, 36(1), 22-29.

Ishak, A., Nazar, R. and Pop, I. (2008). Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Conversion and Management, 49, 3265-3269. Retrieved from https://doi.org/10.1016/j.enconman.2007.11.013

Ishak, A., Nazar, R. and Pop, I. (2008). Uniform suction/blowing effect on flow and heat transfer due to a stretching cylinder. Applied Mathematical Modeling, 32(10), 2059-2066. Retrieved from https://doi.org/10.1016/j.apm.2007.06.036

Lin, H.T. and Shih, Y.P. (1980). Laminar boundary layer heat transfer along static and moving cylinders. Journal of the Chinese Institute of Engineers, 3, 73-79. Retrieved from https://doi.org/10.1080/02533839.1980.9676650

Lin, H.T. and Shih, Y.P. (1981). Buoyancy effects on the laminar boundary layerheat transfer along vertically moving cylinders. Journal of the Chinese Institute of Engineers, 4, 47-51. Retrieved from https://doi.org/10.1080/02533839.1981.9676667

Merkin, J. H., Najib, N., Bachok, N., Ishak, A. and Pop, I. (2017). Stagnation-point flow and heat transfer over an exponentially stretching/shrinking cylinder. Journal of the Taiwan Institute of Chemical Engineers, 74, 65-72. Retrieved from https://doi.org/10.1016/j.jtice.2017.02.008

Mukhopadhyay, S. (2011). Chemically reactive solute transfer in aboundary layer slip flow along a stretching cylinder. Frontiers of Chemical Science and Engineering, 5(3), 385-391. Retrieved from https://doi.org/10.1007/s11705-011-1101-4

Mukhopadhyay, S. (2013). MHD boundary layer slip flow along a stretching cylinder. Ain Shams Engineering Journal, 4, 317-324. Retrieved from https://doi.org/10.1016/j.asej.2012.07.003

Sinha, S. and Yadav, R.S. (2021). Steady MHD mixed convection Newtonian fluid flow along a vertical stretching cylinder embedded in porous medium. International Journal of Engineering Technologies and Management Research, 8(7), 45-57. Retrieved from https://doi.org/10.29121/ijetmr.v8.i7.2021.990

Wang, C.Y. (1998). Fluid flow due to a stretching cylinder. Physics of Fluids, 31(3), 466-468. Retrieved from https://doi.org/10.1063/1.866827

Wang, C.Y. (2002). Flow due to a stretching boundary with partial slip-an exact solution of the Navier-Stokes equations. Chemical Engineering Sciecnce, 57, 3745-3747. Retrieved from https://doi.org/10.1016/S0009-2509(02)00267-1

Xu, H. and Liao, S.J. (2005). Series solutions of unsteady magnetohydrodynamics flows of non-Newtonian fluids caused by an impulsively stretching plate. Journal of Non-Newtonian Fluid Mechanics, 129, 46-55. Retrieved from https://doi.org/10.1016/j.jnnfm.2005.05.005

Yu, S., Yu, P. and Tang, T. (2018). Effect of thermal buoyancy on flow and heat transfer around a permeable circular cylinder with internal heat generation. International Journal of Heat and Mass Transfer, 126, 1143-1163. Retrieved from https://doi.org/10.1016/j.ijheatmasstransfer.2018.06.056